确定空间圆柱面方程的方法探析
(成都师范学院 数学学院,四川 成都 611130)
三维Euclidean空间中都与给定空间曲线C相交的平行直线族所形成的几何体称为柱面,直线族中的每直线称为柱面的一条母线,所有母线具有相同的方向,它称为柱面的方向,定曲线C称为柱面的一条准线[1].若柱面的某一条准线正好是圆周(称为准线圆),则称该柱面为圆柱面[1,2].圆柱面还可等价地描述为“三维Euclidean空间中到定直线的距离等于符号为正的定数的点的全体”,定直线称为圆柱面的轴线,可发现轴线的方向同样也是圆柱面的方向.圆柱面是一类特殊的直纹二次曲面,学习好圆柱面有助于提升学生的空间想象能力与科学计算能力,因此,它是学习与教授“解析几何”课程中的重点;另一方面,因圆柱面的几何结构复杂,是故它也是学习与教授“解析几何”课程中的难点.从多视角研究典型问题能加深对问题的理解,从而克服学习与教授问题所承载知识点过程中的困难[3].
1 问题提出
第一届中国大学生数学竞赛数学专业类预赛[4](2009年)第一题要求考生确定经过三条平行直线的圆柱面的方程,它突出考查应考者的空间想象能力、转化划归能力与科学计算能力,在圆柱面理论中具有极充分的代表性,其内容完整表述如下:
问题(*)设三维Euclidean空间中的圆柱面S同时经过三条两两相互平行的直线:
L1:x=y=z,L2:x-1=y=z+1,L3:x=y+1=z-1,
试确定圆柱面S的方程.
中国大学生数学竞赛由预赛与决赛构成,有数学专业组与非数学专业组之别,每年10月举办预赛,翌年3月举办决赛,首届预赛举办于2009年,实践经验表明,它在大学数学的教学与改革等诸多方向已经取得显著成效,例如,它已帮助提升大学生的学习数学的积极性,已帮助改善大学数学教师的课堂教学质量,已帮助促进高校的大学数学课程质量的提升改革[5,6].作为中国大学生数学竞赛数学专业组预赛中的一道赛题,问题(*)的能力立意突出,既能体现赛事活动的办赛宗旨,又能真实反映出学科学与教的重难点,有鉴于此,问题(*)具有极高的研究价值.经初步分析,笔者发现问题(*)具有多种求解方法,而且每种解法能从一种或多种视角揭示圆柱面的几何特性,从而能帮助加深对圆柱面的理解与认识.本文旨以问题(*)为例,阐述确定三维空间中经过三条平行直线的圆柱面的方程的8种视角下的若干方法.
2 确定圆柱面方程的方法探析
探析1 先确定出圆柱面S的轴线,再利用定义“到轴线的距离等于定数的点的全体”确定出圆柱面S的方程.确定轴线的思路是,由“直线L1,L2,L3上的点到轴线的距离为常数”得出:轴线上的所有点到直线L1,L2,L3的距离都相等.基于这些想法,可得出问题(*)的一种解答.
设直线L是圆柱面S的轴线.任取轴线L上的一点,记其坐标为(x,y,z),因该点到直线L1,L2,L3的距离为常数,故有
或等价地,有
x-1=y+1=z,
此即轴L线的方程.
任取圆柱面S上的一点,记其坐标为(x,y,z),S经过直线L1,而直线L1经过点O(0,0,0),故O点在圆柱面S上,进而得知以(x,y,z)为坐标的点到轴线L的距离与点O到轴线L的距离相等,或等价地,有
经化简整理,得
x2+y2+z2-xy-yz-zx-3x+3y=0.
此即为圆柱面S的方程.

探析2 先确定出圆柱面S的准线圆,再借助于性质“过圆柱面S上任何一点的母线与准线圆相交”确定出圆柱面S的方程.基于这些想法,给出问题(*)的一种解答.
经分析可知,圆柱面S与平面π:x+y+z=0的交线是圆周C,它是圆柱面S的准线圆.直线L1,L2,L3与平面π的交点分别是O(0,0,0),P(1,0,-1),Q(0,-1,1).可验证,以x2+y2+z2-2x+2y=0为方程的二次曲面是经过点O,P,Q的一个球面.于是,准线圆C的方程为
任取圆柱面S上的一点,记其坐标为(x,y,z).设点以(x+t,y+t,z+t)为坐标的点在圆周C上,则
消除参数t,并经化简整理可得
x2+y2+z2-xy-yz-zx-3x+3y=0.
此即为圆柱面S的方程.
探析3 基于探究2的解答过程,可发现确定圆柱面S轴线方程的另一种方法:轴线是直线段OP与OQ的中垂面,其中O(0,0,0),P(1,0,-1),Q(0,-1,1).基于这一想法,给出问题(*)的一种解答.
圆柱面S的轴线L的方程为
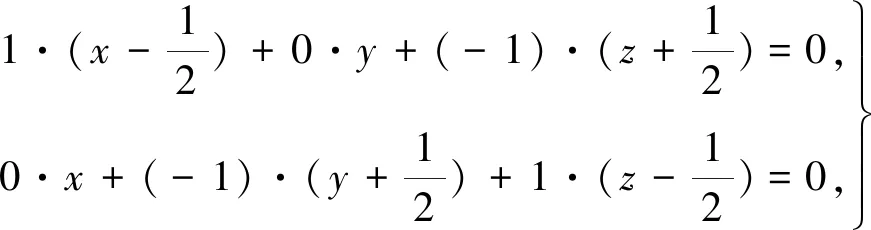
仿照探析1的解答步骤,可得出圆柱面S的方程
x2+y2+z2-xy-yz-zx-3x+3y=0.
注2 因点O(0,0,0),P(1,0,-1),Q(0,-1,1)都是圆柱面S的准线圆上的点,故它们到圆柱面S的轴线上的任何一点的距离相等,利用此发现也可确定出圆柱面S的轴线的方程.
探析4 经计算发现,对任何(x0,y0,z0),(x1,y1,z1)及(m,n,p)∈R3,有
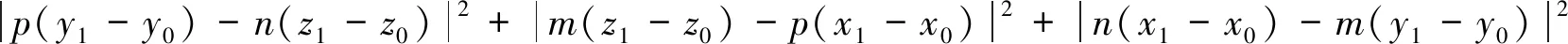
直接利用后者可发现问题(*)的一种解答:
任取圆柱面S上的一点,记其坐标为(x,y,z),因该点到轴线L的距离与点O到轴线L的距离相等,故
经化简整理,得
x2+y2+z2-xy-yz-zx-3x+3y=0.
此即为圆柱面S的方程.
探析5 基于平面系想法,给出问题(*)的一种解答.
设圆柱面S的方程为(x-y)2+(y-z)2+(z-x)2+λ1(x-y)+λ2(y-z)=0,圆柱面S经过直线L2与L3,故以(1,0,-1)与(0,-1,1)为坐标的点都在圆柱面S上,进而有
或等价地,有
由Cramer法则,
于是,圆柱面S的方程为
(x-y)2+(y-z)2+(z-x)2-6(x-y)=0,
或等价地,为
x2+y2+z2-xy-yz-zx-3x+3y=0.
探析6 基于平面系想法,还能给出问题(*)的另一种解答.
设圆柱面S的方程为
因圆柱面S经过直线L1,而直线L1经过点O(0,0,0),故点O在圆柱面S上,进而有
解得,λ=-3.于是,圆柱面S的方程为
或等价地,为
x2+y2+z2-xy-yz-zx-3x+3y=0.
注3 探析5的原理是,先确定出经过直线L1的圆柱面S族的方程,再利用圆柱面S经过直线L2与L3建立方程并借此解出双参数λ1与λ2的值.探析6的想法与探析5类似,先确定出经过直线L2与L3的圆柱面族的方程,再利用圆柱面S经过直线L1建立方程并借此解出单参数λ的值.
探析7 先借助于正交变换,将圆柱面“扶持归正”,此时的圆柱面S′与原来的圆柱面S的形状一模一样,确定出圆柱面S′的方程,最后通过正交变换的逆变换(还是正交变换),得出圆柱面S的方程.能达到上述功能的坐标变换有无穷多,通过取特殊值能获得其中的一个.“扶持归正”圆柱面最大的优点是圆柱面S′的方程在正好也是二维Euclidean空间中的圆周的方程,因此,通过确定圆周方程来达成确定圆柱面S′的方程的目的.基于这些想法,给出问题(*)的一种解答.
借助于正交变换
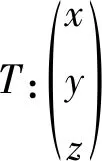
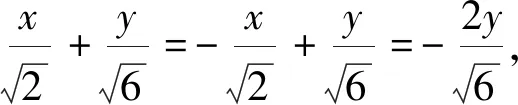
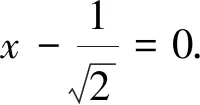
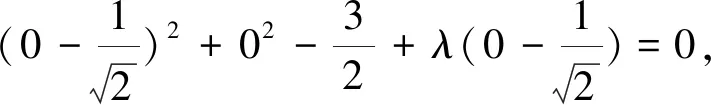
圆柱面S′的方程为
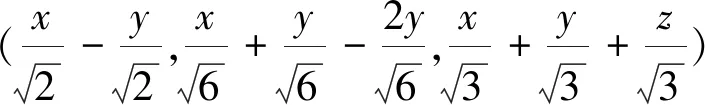
或等价地,有
x2+y2+z2-xy-yz-zx-3x+3y=0,
此即圆柱面S的方程.
探析8 先设出圆柱面S含有待定参数的方程,再利用题设条件建立方程并进而解出待定参数的值.基于这些想法,给出问题(*)的一种解答.
设圆柱面S的方程为
x2+y2+z2+2a12xy+2a23yz+2a13xz+2a14x+2a24y+2a34z+a44=0.
因圆柱面S过直线L1(参数方程为x=t,y=t,z=t),故对∀t∈R,都有
t2+t2+t2+2a12t·t+2a23t·t+2a13t·t+2a14t+2a24t+2a34t+a44=0,
化简整理,得
(3+2a12+2a23+2a13)t2+2(a14+2a24+2a34)t+a44=0.
(1)
类似地,因圆柱面S过直线L2(参数方程为x=t+1,y=t,z=t-1)与L3(参数方程为x=t,y=t-1,z=t+1),故对∀t∈R,有

(2)
由方程(1)与方程组(2)得
基于Gauss消元法,对上述方程组开展初等变换,得

于是圆柱面S的方程为
x2+y2+z2-xy-yz-xz-3x+3y=0.
注4 仿照探析8中发现的思路可证明下述一般性的结论:设某圆柱面S的方向向量为(m,n,p),且其经过三点,已知这三点的坐标分别为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),则圆柱面S的方程为
证设圆柱面S的方程为
x2+y2+z2+2a12xy+2a23yz+2a13xz+2a14x+2a24y+2a34z+a44=0.
根据题设条件,以
(x1+mt,y1+nt,z1+pt),(x2+mt,y2+nt,z2+pt),(x3+mt,y3+nt,z3+pt)
为参数方程的直线都包含于圆柱面S.仿照探析8的解答过程,可证明这等价于:对∀t∈R,有
这事实上还等价于:参数a12,a23,a13,a14,a24,a34,a44满足下述线性方程组
借助于Cramer法则可直接解出参数
a12,a23,a13,a14,a24,a34,a44
的值.
借助于这些,并利用行列式的计算性质,可证得
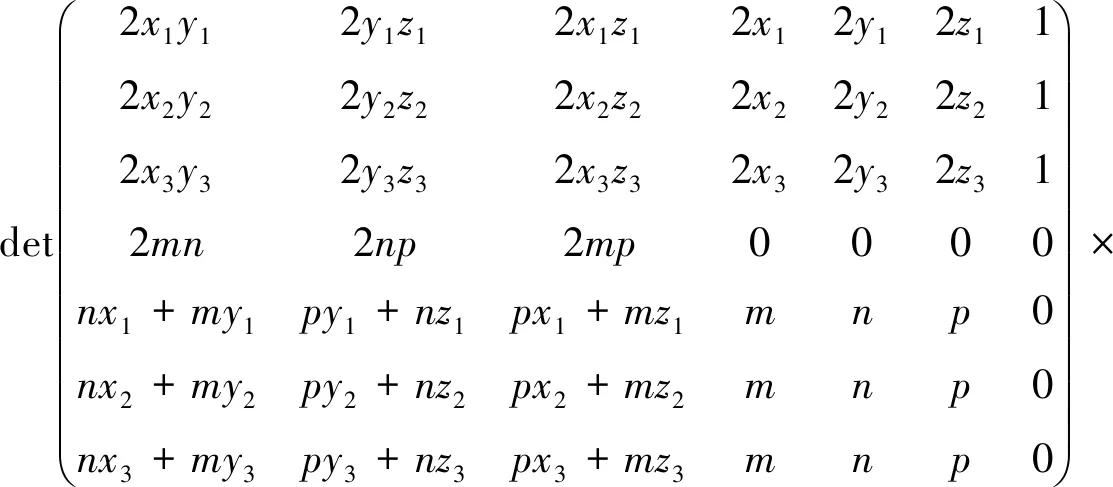
(x2+y2+z2+2a12xy+2a23yz+2a13xz+2a14x+2a24y+2a34z+a44)=0.
注5 借助于注4中发现的公式,
2 结束语
本文以问题(*),即第一届中国大学生数学竞赛数学专业类预赛[4](2009年)第一题为例,从8种视角探析并给出了确定三维Euclidean空间中经过三条平行直线的唯一圆柱面的方程的若干方法.圆柱面是大学“解析几何”课程中的学与教方向的重难点,本文的研究在该方向有重要启示.

