圆柱度的测量方法及其应用
杨建霞
摘 要:探讨了对轴、孔的圆柱度的测量方法,并对圆柱度测量的2种方法(截圆法和螺旋法)进行了分析,有助于在实际工作中找到正确的测量方法,得到可靠的结果。另外,还对螺纹孔位置尺寸的测量方法进行了分析和探讨。
关键词:圆柱面;圆柱度;三坐标测量机;螺纹孔
中图分类号:TG839 文献标识码:A DOI:10.15913/j.cnki.kjycx.2017.03.125
在机械制造行业中,有许多轴、孔类零件对横、轴剖面形状精度要求比较高,比如液压柱、汽缸里的阀杆及各种驱动主轴轴颈等,都是以圆柱度误差来控制的。圆柱度是一项控制圆柱面精度的综合指标,它的定义考虑了某些高精度产品的使用要求,因而用它来控制圆柱面精度是比较理想的。另外,有些零件,比如大齿轮、缸体、缸盖、变速箱壳体等,其表面布满空间孔系,各孔的位置尺寸、形状公差和位置公差必须得到保证,才能满足装配的互换性。
1 “圆柱度”概念的理解
1.1 圆柱度公差带
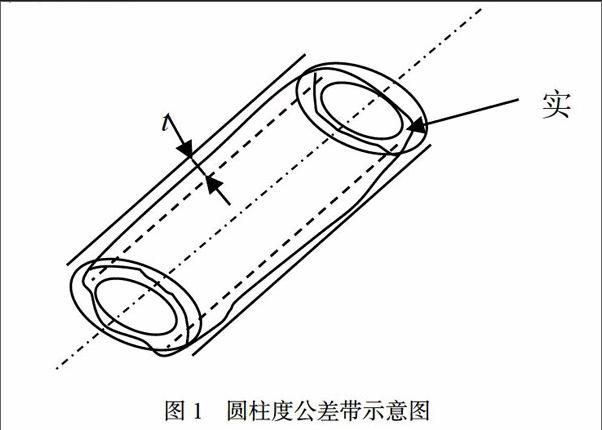
圆柱度公差带是半径差为公差值t的两同轴圆柱面之间的区域,如图1所示。
圆柱度是形状公差的一个项目。所谓“形状公差”,是指被测要素对理想要素的变动量。理想要素要符合最小条件,即被测要素对理想要素的最大变动量为最小。圆柱度误差是控制圆柱的纵、横剖面及轴心线的圆度、直线度和平行度的综合指标。圆柱度公差是指包容实际表面,而且半径为最小的两同轴圆柱面的半径差。
1.2 “轴”“孔形状公差”等概念的区别
圆度是指圆柱横剖面的单项指标,圆柱母线平行度是圆柱轴剖面的单项指标,圆柱轴心线直线度是指圆柱轴心线在任意方向(空间360°范围内)都要控制轴心线的直线度。在实际中还会遇到“锥形度”这一概念,它是指圆柱在某一个轴向的直径变化。根据定义,它们都有严格的区别,量值上也没有换算关系。圆柱的圆度、母线平行度合格,圆柱度不一定合格。因为它们都不能控制轴心线的直线度。因此,要控制圆柱面的高精度,必须采用圆柱度公差。
2 评定圆柱圆柱度公差的几种方法
2.1 最小区域法
最小区域法评定圆柱度误差,是由半径差最小的两个同轴圆柱面包容被测表面,其半径差即为圆柱度误差。包容时,使内圆柱面和外圆柱面分别与圆柱面有3点接触,以构成最小区域。此方法评定圆柱度误差是符合公差体系标准要求的。这种方法是否准确、可靠,关键在于测量手段是否符合或接近最小条件。
2.2 最小外接圆中心法
最小外接圆中心法是用最小外圆柱面包容被测表面,与被测表面最凸出的地方至少有2点接触。由实际被测表面至最小外接圆柱面的最大距离作为圆柱度误差值。此方法可以用来评定轴类外表面的圆柱度。它相当于一只精度很高的环规与轴密配,经多次测量间隙的最大值为其圆柱度公差。
2.3 最大内接圆中心法
最大內接圆中心法是用实际被测表面至最大内接圆圆柱面的最大距离作为圆柱度误差值。此方法可以用来评定孔类外表面的圆柱度。它相当于一只精度很高的塞规与孔密配,经多次测量间隙的最大值为其圆柱度公差。
上述3种方法在评定圆柱度公差时比较复杂,在实际工作中,采用近似的方法来确定理想要素的位置,比如用数学中的最小二乘法来拟合实现理想要素。在圆柱度测量技术中,理想要素就是圆柱面的轴心线。这也是我们测量圆柱度公差的关键。
3 三坐标测量机测量圆柱度公差的方法
3.1 垂直轴线的截面圆法
这种方法反映了各截面圆圆心的弥散和半径波动情况,它往往不能反映整个圆柱表面的误差。因此,在实际测量过程中,应多取几个截面圆(至少3个),覆盖整个圆柱长度,确保测量精度。对于比较长的圆柱测量精度高,该方法是比较好的测量方法。
3.2 螺旋形采点法
在靠近圆柱一端的地方,且在同一截面上至少采3点,其他各点在圆柱表面按螺旋顺序采集,至少应在3点以上,而且要覆盖整个圆柱长度。对于比较短的圆柱测量精度高,体现了圆柱精度较高的回转和直线运动。
4 圆柱度的测量方法应用
圆柱度的测量方法应用,即螺纹孔位置尺寸的测量。在生产实践中,测量光孔的位置很稳定,而测量螺纹孔的位置却很不稳定。测量连续加工的3个零件同一位置尺寸,相差很大,经常出现一个合格,而另一个不合格的情况,给生产部门、维修部门造成很大的困难。目前,在三坐标测量机上测量螺纹孔有以下3种方法:①在螺纹孔中加装螺纹芯轴,在芯轴上采点测量。这种测量方法误差的主要原因是螺纹芯轴将螺纹孔的轴心线延长,以及螺纹配合误差的存在。这就会造成多次测量结果的散差很大。②在螺纹孔同一截面上采点。这种测量方法误差的主要原因是同一截面上采点构成的圆不在螺纹孔的轴心线上,而且在不同的地方测圆,其圆心偏离轴心线的距离有很大的区别。③沿螺纹孔中螺纹的旋转方向步进采点。这种测量方法保证了所采点构成的圆的圆心在螺纹孔的轴心线上,在评价其位置尺寸时误差最小。
5 结束语
在实践中,应充分理解和掌握形状和位置公差的国家标准,运用统计分析技术不断探索形状和位置公差的测量技术,提高测量精度,才能为生产、工艺改进提供科学、可靠的依据。
参考文献
[1]〔德〕G.Henzold.形位公差:在设计、制造及检验中的应用[M].北京:中国计量出版社,1997.
[2]张国雄.三坐标测量机[M].天津:天津大学出版社,1999.
〔编辑:刘晓芳〕

