随机共振模型结构参数自寻优方法与应用

明廷锋，张永祥，李 婧

随机共振模型结构参数自寻优方法与应用

明廷锋，张永祥，李 婧

(海军工程大学动力工程学院，武汉 430033)

在随机共振微弱周期信号检测过程中，如何确定结构参数值非常关键．已有的结构参数选择方法在应用上存在着局限性，如由于模型输入信号的干扰噪声未知，通常定义的信噪比无法获得．针对该问题，首先改写了随机共振模型的数学表达式；然后定义了一种随机共振模型输出信噪比，并给出了计算方法；最后在此基础上，以输出信噪比为评价指标，提出了一种结构参数自寻优方法，用于构建性能优良的随机共振模型．仿真信号分析表明该方法能较好地解决输入信号背景噪声未知的问题，所构建的随机共振模型可有效检测出低频率和高频率的微弱周期信号．通过对转子试验装置上的转子系统早期不平衡故障分析的应用，验证了所提出方法的有效性和实用性．

随机共振；结构参数寻优；微弱周期信号检测；故障诊断

具有双势阱性质的朗之万方程(Langevin equation，LE)是一种最典型、最简单的非线性双稳态系统描述方程之一，常用于研究随机共振(stochastic resonance，SR)现象，在微弱信号检测、机械故障分析等领域中得到了应用．随机共振模型(简称SR模型)中结构参数a和b取值不同，对模型的特性影响较大，将直接导致随机共振状态性能的优劣．文献[1]探讨了影响和产生双稳系统随机共振的参数特性，仿真分析表明通过适当的参数选择可得到最佳的随机共振状态；文献[2]系统地分析了双稳系统阈值与SR模型的结构参数a和b的关系，得出结构参数对随机共振现象发生起着决定性作用的结论．结构参数的改变会引起双稳系统的势垒、势阱间距和粒子跃迁速率的改变，并使噪声能量相对地重新分配，形成噪声量相对“不足”或“过剩”，近而影响随机共振效果．当不断增大a或减小b时，会使随机共振状态转变为“欠共振”的状态，而不断减小a或增大b时，则会导致“过共振”状态．因此，结构参数的优化选择方法成为研究的关键问题之一．文献[3]认为当采样频率fs一定时，fs如果不能严格为信号频率f0的50倍，则二次采样随机共振技术就有可能失效；探讨了采用扫频采样技术寻找被测设备的频率特征，但是文中没有给出结构参数调整方法以及二次采样频率的选取过程．文献[4]给出了一种自适应参数调节的随机共振微弱信号检测方法．该方法是在基于背景噪声已知的前提下提出的，其工程应用也是在理想的转子系统早期碰摩故障信号中人为加载噪声仿真信号情况下取得的试验结果．随后，先后出现了几种采用基于进化算法的自适应随机共振算法，从而对随机共振系统的多个结构参数进行同步优化．例如，文献[5-6]分别采用了基于遗传算法和蚁群算法．上述两种方法都是通过定义一个信噪比作为评价函数，但是文中的信噪比定义不太明确，结构参数优化过程需要较多的训练样本，且随着设备运行状态的波动，得到的优化参数会存在不适用的情况．

笔者在分析和参考该领域相关研究成果的基础上，给出一种SR模型结构参数自寻优方法，目的在于根据输入信号的特性实现自动寻找最优结构参数，构建性能优良的SR模型，从而实现机械设备故障分析过程中微弱周期信号的有效检测．

1 SR模型的参数自寻优方法

1.1 基于参数自寻优方法的SR模型

在受到随机噪声n(t)和外部周期驱动力f(t)的共同作用下，非线性双稳态系统的SR模型[7]表示为

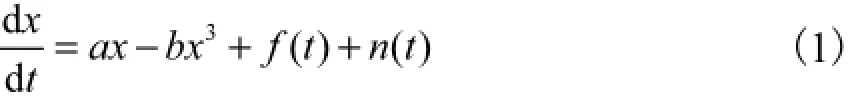
式中：a和b为SR模型的结构参数，是正实数；t为时间历程；f(t)=Asin(2πf1,t)，在工程应用情况下，f(t)即为幅值为A、频率为f1的有用周期信号；n(t)的统计平均值为E[n(t)]=0，相关矩为E[n(t)n(t′)]= 2,Dδ(t-t′)．

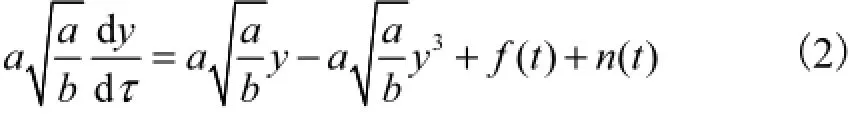
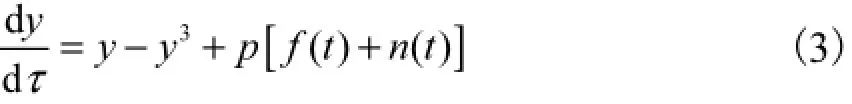
式(3)即为SR模型的另一种数学表达式，其中f(t)+n(t)是SR模型的输入信号s(t)，在实际应用中为实测信号，也即为待检测信号．可见，经过推导后，SR模型需调整的结构参数由两个(a和b)变成了一个(p)，从而简化了结构参数寻优的实现过程．而式(3)中τ的定义，使得该SR模型不仅仅适用于低频率的待检测信号，而且适用于任意频率的信号．其做法是通过选择合适的a值，在时间轴上对高频信号进行尺度拉伸变化，将高频率信号转化为SR模型适用的频率信号．显然，这种尺度变化实现起来方便，容易确定时间尺度变换参数a值．因此，关键问题就在于如何寻找参数p的最优值．

1.2 参数寻优的评价指标

SR模型结构参数最优值选择过程中，最直接的方法就是利用SR模型输出的信噪比作为评价指标．文献[8]虽然提出了利用信号的近似熵距离矩阵中的最小值来设定参数a和b的方法，但是前提也是通过定义一个信噪比，获得信噪比与近似熵的关系．与文献[4-6]相似，所给出的信噪比定义需要背景噪声特性已知，这与实际工程应用不符，因为实际工程过程中采集到的信号是背景噪声与有用信号的混合，显然其特性是难以获知的．

本文在进行SR模型参数寻优过程中，采用一种模型的输出信号的信噪比作为评价指标，使得信噪比达到最佳的参数p即为所求．考虑到信号(包含噪声)在采集过程中可能会出现设备瞬时转速波动以及频域变换时的计算误差，这里定义一种模型输出信噪比，即为尺度变换后信号待测的频率f0附近频率段的幅值谱之和与全频段的幅值谱之和的比值．其数值计算式为

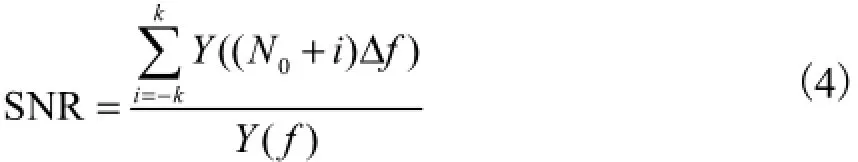
式中：()Yf为SR模型输出信号y(τ)的幅值谱；Δf为频率分辨率，尺度变换后输入信号的待测频率为f0；N0为对应的谱线数，则f0=N0,Δf；k为整数．

1.3 参数自寻优方法

估计待检测信号s(t)的频率为f1，根据上述分析和定义，可得到以下SR模型的参数p自寻优方法，其算法如图1所示．

(1) 根据f1的大小，确定合适的时间尺度变换参a，并在时间轴上进行尺度变换，得到信号s(τ)，τ=at；

(2) 设定p的取值范围及计算步长Δp，p=p0+ iΔp，(i=0，1，…，M)；

(3) 将信号s(τ)输入结构参数为p的SR模型(其数学表达式见式(3))，计算得到输出信号y(τ)；

(4) 先计算y(τ)的幅值谱Y(f)，再计算信噪比SNR；

(5) 重复步骤(2)～(4)，直至获取所有的SNR值；

(6) 求取其中最佳的SNR值，其对应的结构参数值即为最优p值．

至此，参数寻优过程完成，同时通过SR模型的信号检测过程也完成，只需要在频率轴上进行尺度恢复，即可进行微弱信号检测、故障分析等．

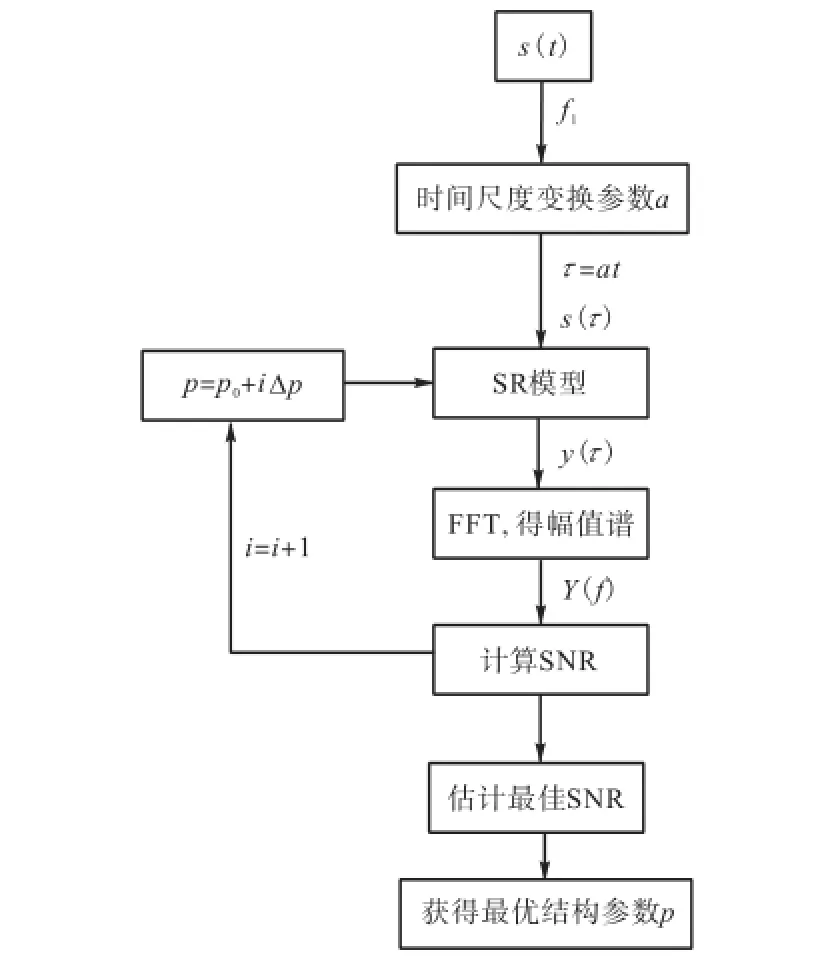
图1 SR模型的参数自寻优算法Fig.1 Algorithm of parameter self-optimization in SR model

2 仿真信号分析

本节从低频率和高频率两种情况进行仿真信号分析，说明和验证SR模型参数自寻优方法在微弱周期信号检测中的有效性．

2.1 低频率的仿真信号分析

设输入信号为s(t)=Asin(2πft)+n(t)，其中n(t)是均值为0、噪声强度为D的高斯分布白噪声．这里取A=0.1，f=0.04,Hz，D=1．信号时域与幅值谱图如图2所示，由于信噪比太低，0.04,Hz的周期分量无法识别．如图3所示，使用结构参数为a=1和b=1的SR模型进行信号检测，虽然经过SR模型的输出信号在时域上呈现一定的周期特性，幅值谱图的高频分量被抑制，但是仍无法识别出该周期分量．应用本文提出的方法进行参数p的自寻优，从图4中可见，随着p值的变化，评价指标SNR由渐增变为递减过程．取输出信噪比最佳的时候，即p=1.26时的SR模型．如图5所示，从其输出幅值谱图中可明显识别出0.04,Hz的周期分量．

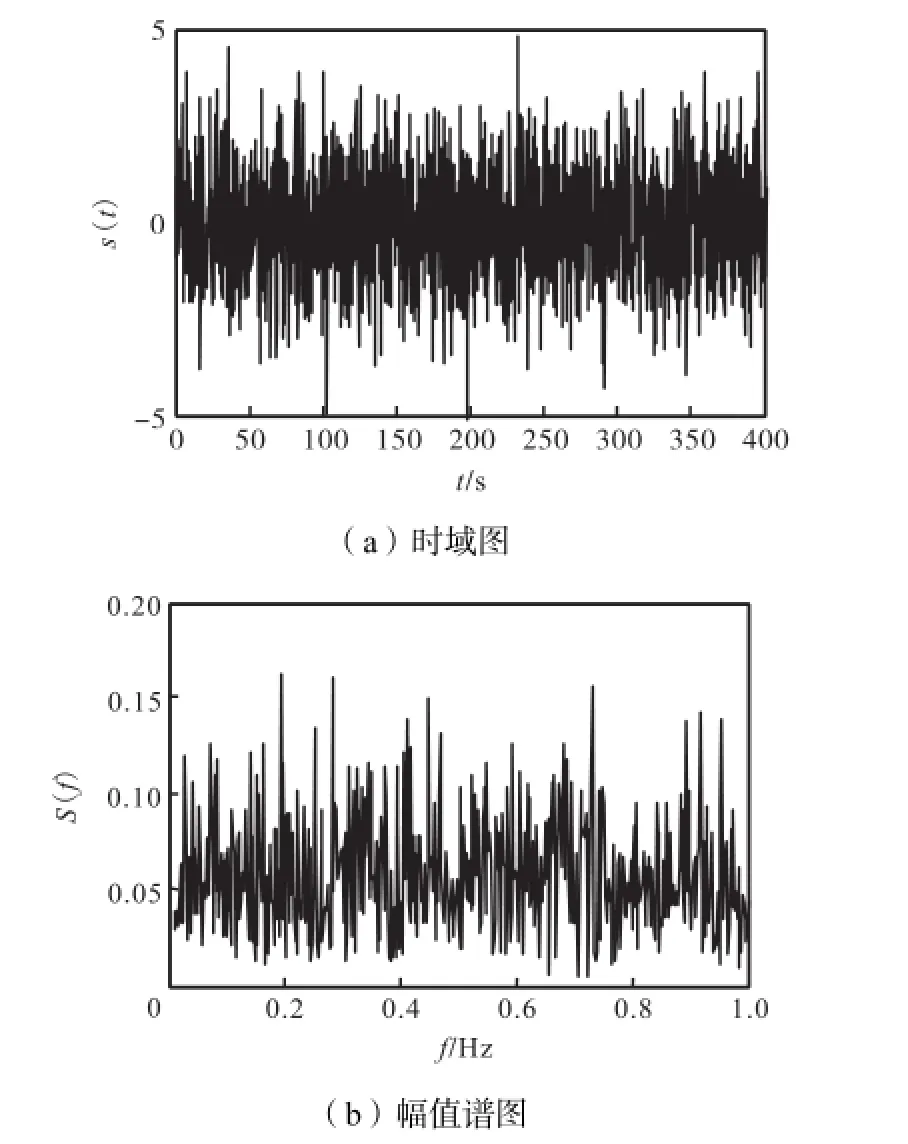
图2 输入信号的时域图和幅值谱图(低频率)Fig.2Time domain and amplitude spectrum of input signals(low frequency)

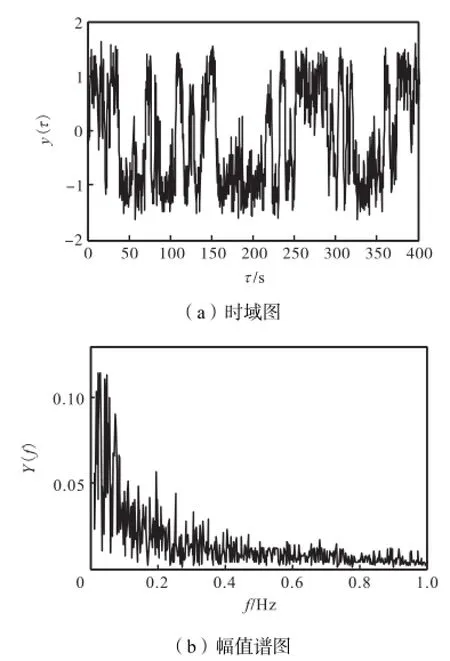
图3 输出信号的时域与幅值谱图(a=1，b=1)Fig.3Time domain and amplitude spectrum of output signals(a=1，b=1)

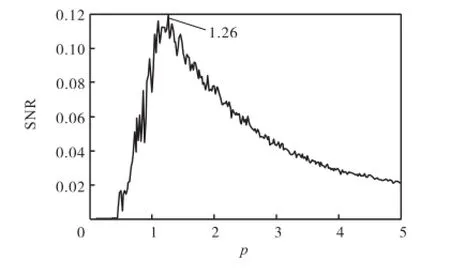
图4 参数p的寻优过程(p=1.26)Fig.4 Optimizing process of parameter p(p=1.26)

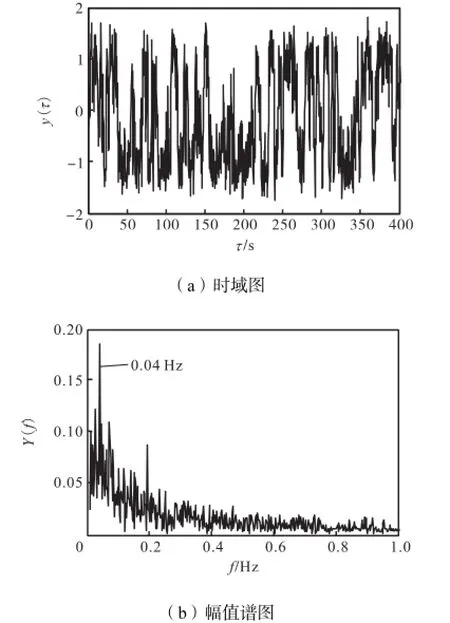
图5 输出信号时域与幅值谱图(p=1.26)Fig.5 Time domain and amplitude spectrum of output signals(p=1.26)

2.2 高频率的仿真信号分析

采用同样形式的仿真信号，同样取A=0.1，D= 1，而信号频率f=80,Hz．时间尺度变换参数a= 2,000．图6和图7分别为仿真信号的经SR模型(p= 1.22)处理前后的信号时域波形和幅值谱．可见，图6中得不到80,Hz的周期成分，而图7中则可识别出80,Hz的周期分量(已经过尺度恢复处理)，即为待检的信号频率．图8给出了参数p的寻优过程．

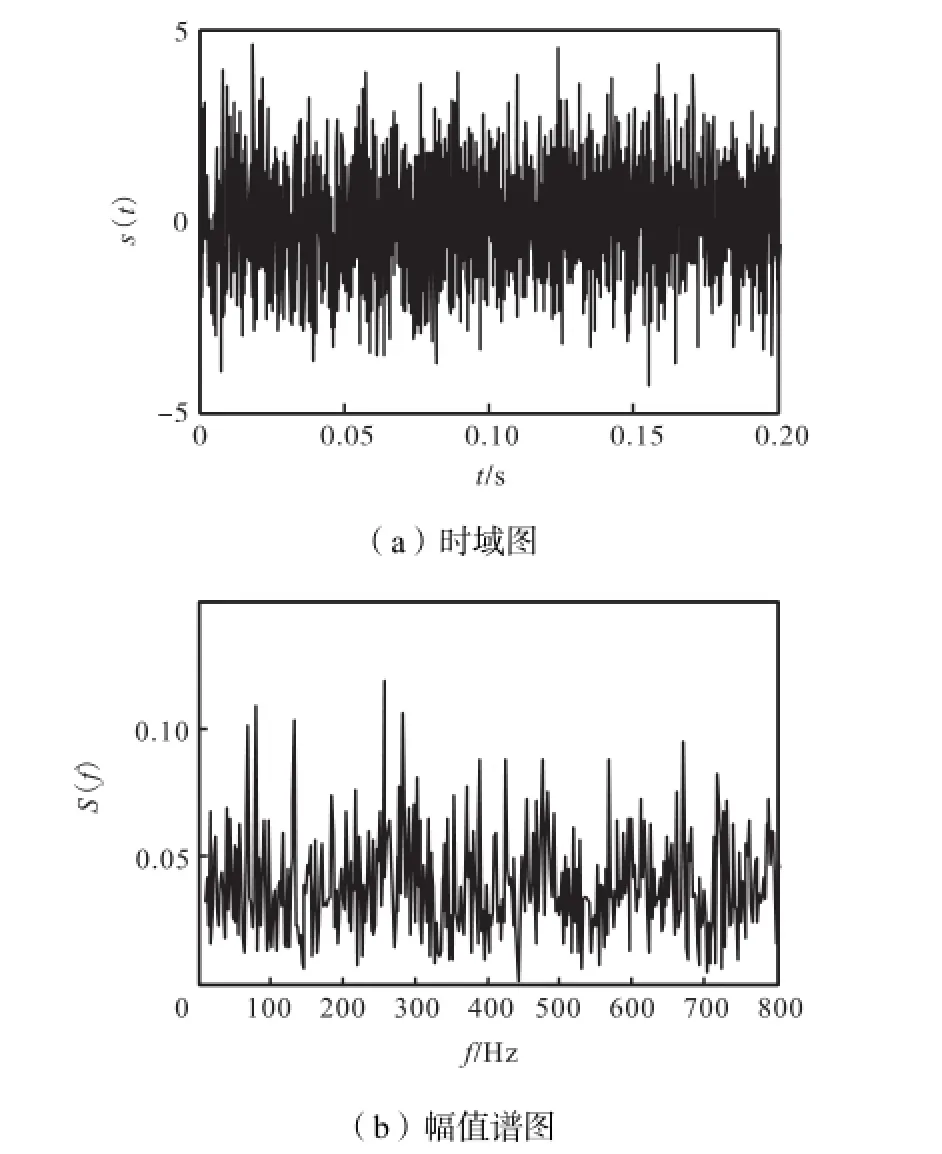
图6 输入信号的时域图和幅值谱图(高频率)Fig.6Time domain and amplitude spectrum of input signals(high frequency)

图7 输出信号时域与幅值谱图(p=1.22)Fig.7Time domain and amplitude spectrum of output signals(p=1.22)

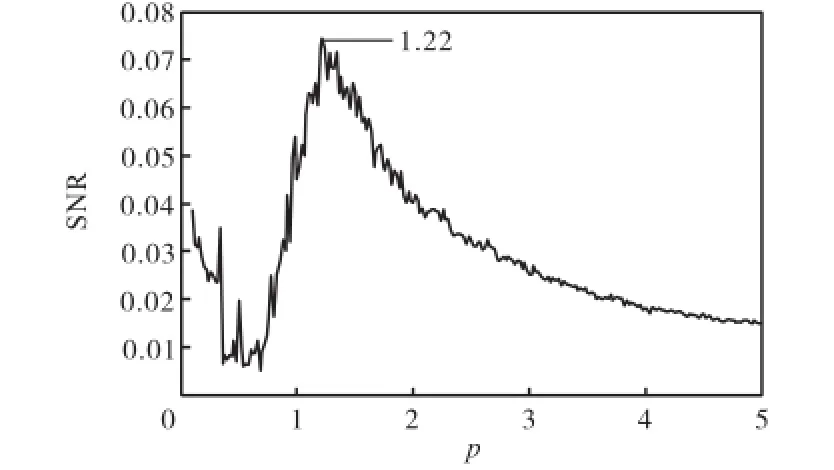
图8 参数p的寻优过程(p=1.22)Fig.8 Optimizing process of parameter p(p=1.22)

3 在转子试验装置故障检测中的应用

试验在多功能转子试验装置上进行，该装置由电机、转速控制器、测速齿轮、联轴节、转轴、转子和台架等部件组成．转子为一直径为120,mm、厚度为10,mm的金属圆盘，通过在其侧表面预设的安装孔处加装4.942,g的质量块，来模拟转子系统的早期不平衡故障．让转子系统工作在约2,400,r/min，并通过B&K 3560,C振动噪声测试仪采集了该装置的振动加速度信号．采样频率设为4,096,Hz，采样时间长度为2,s．

当转子系统出现质量不平衡故障时，其振动信号在时域波形上表现为简谐振动形式，在频域上转频的1倍频能量较大，谱图形式简单．但在干扰信号较强、不平衡质量较小的情况下，上述谱图特征将难以呈现，导致故障诊断失败，如图9所示．

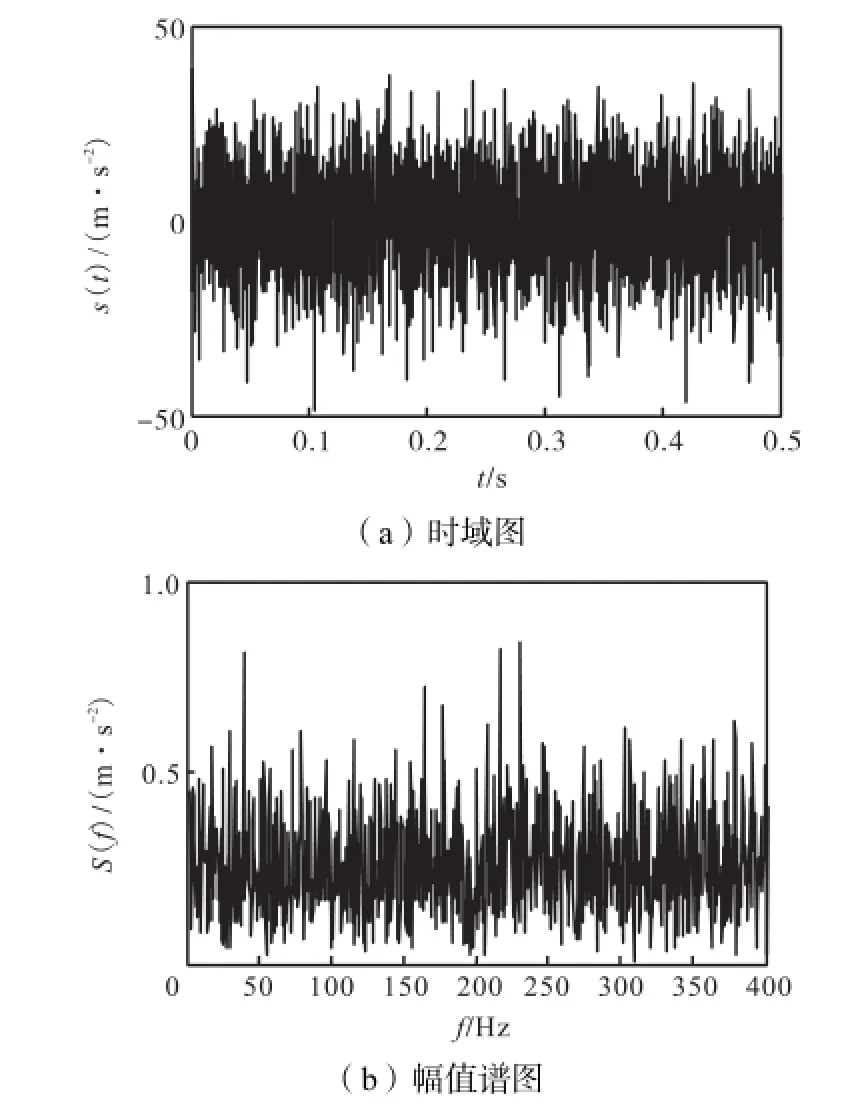
图9 转子系统的振动加速度信号Fig.9 Vibration acceleration signals of the rotor system

应用前述结构参数自寻优方法，经过寻优过程计算(如图10所示)，构建了参数p=0.13的SR模型，并进行了转子试验装置的振动信号分析．从图11可见，时域波形所表现的周期性并不明显，仍存在较大的干扰成分；但其幅值谱图则可明显辨识出39.5,Hz的频率分量，正好与不平衡的频谱特征相符．

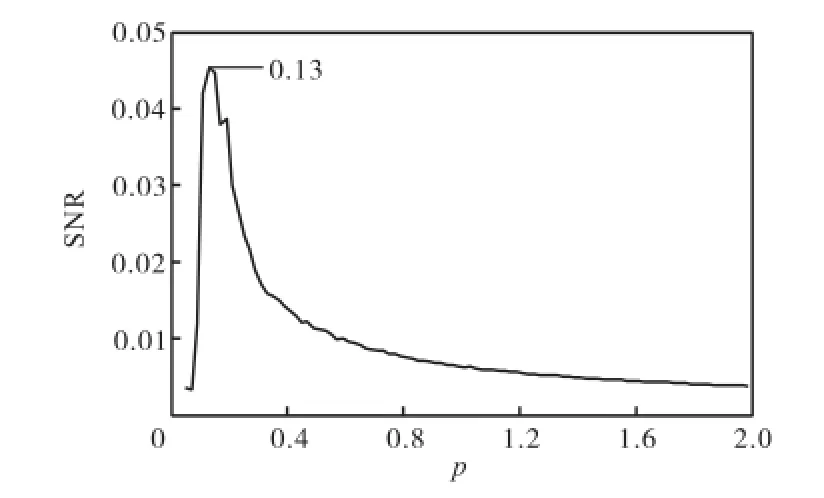
图10 参数p的寻优过程(p=0.13)Fig.10 Optimizing process of parameter p(p=0.13)

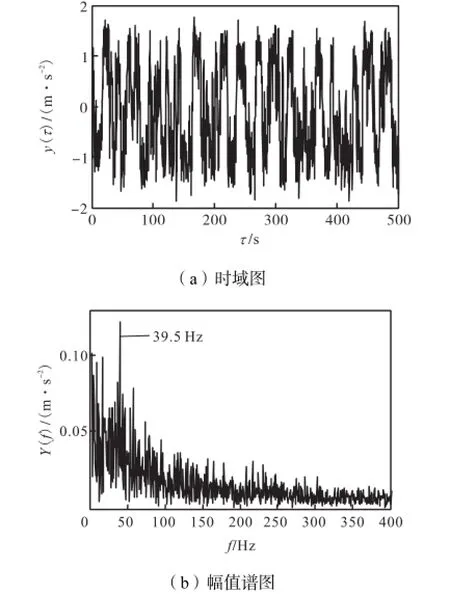
图11 输出振动加速度信号时域与幅值谱图(p=0.13)Fig.11 Time domain and amplitude spectrum of output vibration acceleration signals(p=0.13)

为了更好地进行故障分析，这里对该模型输出信号做级联SR处理．以前面构建的SR模型作为一级，其输出信号作为二级级联SR模型的输入，通过自寻优过程建立二级级联SR模型，此时结构参数用p2表示，p2=1.31．信号处理结果如图12所示，时域波形得到了明显改善，信号的周期特性明显；幅值谱中39.5,Hz特征分量的能量得到了明显加强，50,Hz以上的噪声干扰被进一步抑制．

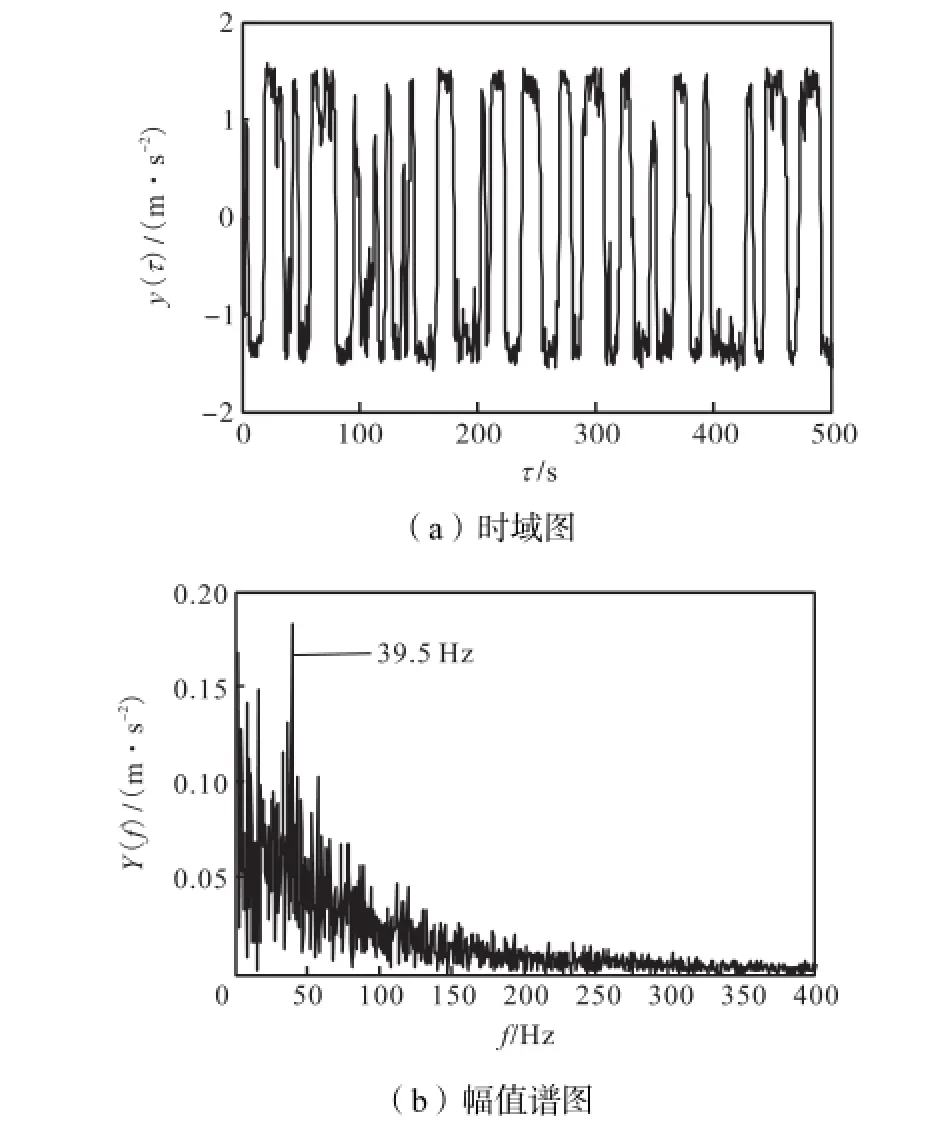
图12 级联SR的振动加速度信号时域与幅值谱图Fig.12 Time domain and amplitude spectrum of output vibration acceleration signals in cascaded bistable SR model

4 结 论

(1) 文中定义的SR模型信噪比计算方法符合工程实际，具有较强的适用性，可作为模型参数选择过程中的评价指标．

(2) 仿真信号分析表明，无论对于低频率还是高频率，提出的SR模型结构参数自寻优方法都可较好地检测出弱周期分量；通过对转子试验装置上的振动加速度信号的分析试验，进一步证实了该方法的有效性和实用性．

(3) 采用了基于本文提出的参数自寻优方法的级联SR，对转子系统的振动加速度信号进行了分析处理，结果表明利用级联SR的滤波特性，不但可以进一步消除信号的高频噪声，还可以加强低频特征信号的能量，提高了信噪比．

［1］ 冷永刚，王太勇，郭 焱，等. 双稳随机共振参数特性的研究[J]. 物理学报，2007，56(1)：30-35.

Leng Yonggang，Wang Taiyong，Guo Yan，et al. Study of the property of the parameters of bistable stochastic resonance [J]. Acta Physica Sinica，2007，56(1)：30-35(in Chinese).

［2］ 石 硕，李谨言，顾学迈. 双稳态系统中结构参数对系统性能的影响[J]. 科学技术与工程，2011，11 (27)：6631-6636.

Shi Shuo，Li Jinyan，Gu Xuemai. Effects of structure parameters on the bistable system performance [J]. Science Technology and Engineering，2011，11(27)：6631-6636(in Chinese).

［3］ 邓学欣，王太勇，冷永刚，等. 自适应扫频随机共振方法的研究[J]. 西安交通大学学报，2005，39(1)：108-110.

Deng Xuexin，Wang Taiyong，Leng Yonggang，et al. Study on adaptive swept stochastic resonance algorithm [J]. Journal of Xi’an Jiaotong University，2005，39(1)：108-110(in Chinese).

［4］ 陈 敏，胡茑庆，秦国军，等. 参数调节随机共振在机械系统早期故障检测中的应用[J]. 机械工程学报，2009，45(4)：131-135.

Chen Min，Hu Niaoqing，Qin Guojun，et al. Application of parameter-tuning stochastic resonance for detecting early mechanical faults [J]. Journal of Mechanical Engineering，2009，45(4)：131-135(in Chinese)．,

［5］ 王 晶，张 庆，梁 霖，等. 采用遗传算法的自适应随机共振系统弱信号检测方法研究[J]. 西安交通大学学报，2010，44(3)：32-36.

Wang Jing，Zhang Qing，Liang Lin，et al. Adaptive stochastic resonance based on genetic algorithm with applications in weak signal detection [J]. Journal of Xi’an Jiaotong University，2010，44(3)：32-36(in Chinese).

［6］ 雷亚国，韩 冬，林 京，等. 自适应随机共振新方法及其在故障诊断中的应用[J]. 机械工程学报，2012，48(7)：62-67.

Lei Yaguo，Han Dong，Lin Jing，et al. New adaptive stochastic resonance method and its application to fault diagnosis [J]. Journal of Mechanical Engineering，2012，48(7)：62-67(in Chinese).

［7］ 何正嘉，陈 进，王太勇，等. 机械故障诊断理论及应用[M]. 北京：高等教育出版社，2010.

He Zhengjia，Chen Jin，Wang Taiyong，et al. Theories and Applications of Machinery Fault Diagnostics[M]. Beijing：Higher Education Press，2010(in Chinese).

［8］ 李 强，王太勇，冷永刚，等. 基于近似熵测度的自适应随机共振研究[J]. 物理学报，2007，56(12)：6803-6808.

Li Qiang，Wang Taiyong，Leng Yonggang，et al. Research of adaptive stochastic resonance based on approximated entropy [J]. Acta Physica Sinica，2007，56(12)：6803-6808(in Chinese).

（责任编辑：赵艳静）

Parameter Self-Optimizing Method and Its Application of Stochastic Resonance Model

Ming Tingfeng，Zhang Yongxiang，Li Jing
(College of Power Engineering，Naval University of Engineering，Wuhan 430033，China)

Determining the value of the structure parameters plays a key role in the weak periodical signal detection by the stochastic resonance technology. The existing parameter-choosing methods show some limitations in application. For example，because the interference noise of the model input signal is unknown，the signal-to-noise ratio cannot be obtained. To solve this problem mentioned above，firstly，a new mathematical expression of the stochastic resonance model is proposed. Secondly，the signal-to-noise ratio of the modelis redefined and its calculation process is provided. Finally，a structure parameter self-optimizing method using the output signal-to-noise ratio as the evaluation index is presented for designing the stochastic resonance model with excellent performance. The simulation data processing results indicate that the difficulty in obtaining the signal-to-noise ratio can be resolved by the method proposed. And the constructed model can be used to successfully extract the weak periodical signals with both the low and high frequency. Also the early imbalanced fault diagnosis in the rotor system demonstrates the effectiveness and practicality of the presented self-optimizing method.

stochastic resonance；structure parameter optimization；weak periodical signal detection；fault diagnosis

TP206

A

0493-2137(2014)10-0886-06

10.11784/tdxbz201307015

2013-07-07；

2013-11-08.

国防预研基金重点资助项目(9140A27020413JB11001)；海军工程大学自然科学基金资助项目(HGDQNJJ12009).

明廷锋（1975— ），男，博士，副教授.

明廷锋，hgming@126.com.

时间：2013-11-22.

http：//www.cnki.net/kcms/detail/12.1127.N.20131122.1102.007.html.