对基于模糊PID的足球机器人电机控制系统设计研究

董娜娜

摘 要：针对机器人运动的时变、非线性、干扰大、不确定等特性，本文在传统PID控制基础上提出了一种与模糊控制器相结合的混合型模糊PID控制方法。该方法弥补了传统PID控制所需精确数学模型、参数整定困难等不足，保证了系统的快速性、稳定性和灵活性。

关键词：模糊PID；角度控制；仿真

1.控制系统结构

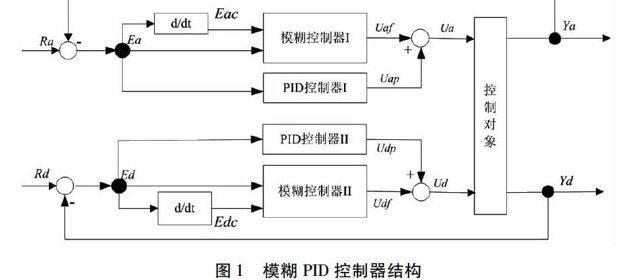
本系统中由于机器人的运动涉及到角度及距离两个方面，所以本文中的模糊PID控制器具體设计为两组控制器构成：一组用于控制机器人的角度转动，一组用于机器人的位置移动。具体结构图如图1所示。

其中Ra、Ya为角度的输入输出，Ea、Eac为角度误差及其变化率，Uaf、Uap为角度模糊控制器和PID控制器输出，Ua为角度控制器总输出。同理，位置的控制输出也是如此。下面进一步以电机角度的模糊PID控制为例来说明系统的可行性。

2.模糊控制器的设计

设在采样时刻t，误差和误差的变化分别为：

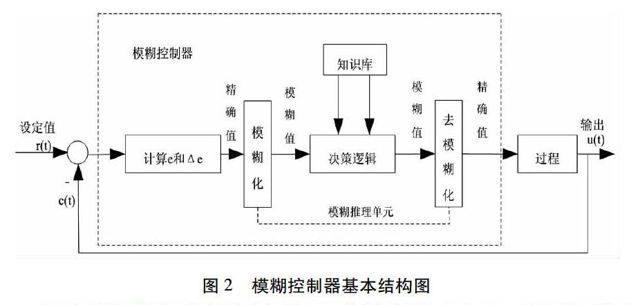
本模糊系统设计为二维控制器：et、Δet为两个输入变量，ut为输出变量。模糊控制器的基本结构如下图2所示。

从上述控制器的系统设计中知道PID控制器的输出为Uap，模糊控制器的输出为Uaf，故总输出为Ua=Uap+Uaf=KP×et+Ki×∫etdt+Uaf 。

根据模糊控制规律本文设计系统中没有微分环节，而参数Kp、Ki是通过实验方法确定的。从角度和距离的实际情况中我们可以看出，不同范围的误差变化，系统要取得好的控制效果，Kp、Ki参数是不同的。例如，在角度控制中，Kp适合于误差为10o到20o的中等角度，但它对5o以下的小角度调节时，Kp×et就会过小，从而使得调节时间较长、稳态误差增大；但在对40o以上的大角度调节时，Kp×et就会过大而出现较大的超调，调节时间也相应延长。所以针对这样的情况，在本论文中的PID控制器的设计针对不同范围的误差，采用了多组参数值的方法。将角度误差范围分为小（0-5o），中（5o-25o）、大（25o以上）3个区域，每个区域对应不同的参数值。经过实验，本论文中的小角度误差时Kp取0.65，Ki取0.0015；中角度时Kp取0.35，Ki取0.0015；大角度时Kp取0.15，Ki取0.001。

3.实验结果分析

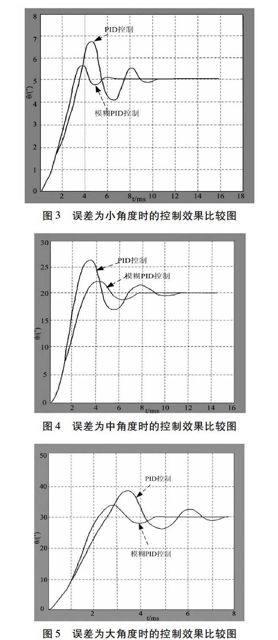
本系统的实验是利用MATLAB的Simulink仿真环境对系统进行的。下图3、4、5就是角度范围划分不同情况下单一的PID控制与模糊PID控制的效果对比图。

实验结果分析：

（1）从图3和图4可以看出，在单一的PID控制输出超调量较大时，引入模糊控制后，确保快速性的情况下能够减小系统输出的超调量。

（2）从图5可以看出，在单一的PID控制输出调节时间过长时，引入模糊控制后，确保不损失控制精度的情况下，能迅速减小调节时间。

4.总结

通过实验对本文所提出的模糊控制器与单一PID控制器相结合构成的模糊PID控制算法进行了测试，并通过仿真曲线图形显示了模糊PID控制算法能够保证机器人足球系统运动控制的准确性和稳定性，又缩短了动态调整时间，取得了较好的控制效果。（作者单位：长春工业大学人文信息学院）

参考文献：

[1] 诸静.模糊控制理论与系统原理[M].北京：机械工业出版社，2005.

[2] 李琳，曾孟雄.模糊PID控制在运动控制中的应用[J].机械与电子，2006（2）.

[3] 田琦，李琪，姚鹏，赵媛.基于模糊PID的全方位移动机器人运动控制[J].电子科技，2011（9）.