基于模糊PID的液压调平系统的同步控制研究
李德刚
【摘要】 针对载重平台液压调平控制的特点,建立了载重平台的数学模型,在AMESim软件中对组成平台调平中液压缸同步控制结构的主要元件进行了建模,引入模糊PID控制策略,设计了模糊PID控制器,目的是使模糊PID控制能够提高系统控制性能。
【关键词】 液压调平 模糊PID AMESim
引言
在现代民用工业领域如物料运输、矿井开采、机械制造等方面,以及以及军事工程领域中如导弹发射、雷达搜索等环节中,往往对各类载重平台在作业过程中有水平度的要求,载重平台的调平一般选用液压调平方式来完成[1],而在这个过程中,最重要的就是解决液压支腿同步控制的问题。
一、液压调平控制系统设计
1.1系统的结构与组成
载重平台调平系统一般采用闭环控制的结构设计,反馈的输出量可以提高调平的同步精度和自动化程度[2]。由信号采集装置将采集到的输入信号以及反馈信号传给控制器,控制器依据设定的要求来对执行机构进行控制,最后由执行机构(液压缸)驱动载重平台动作使得其达到水平状态且无虚腿。其结构如图1所示: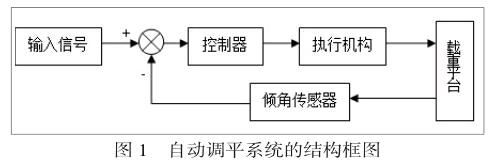
1.2调平策略的选择
在刚性液压平台的调平过程中,由于支腿在运动方向上只有一个自由度,其受到平台牵引而形成的运动轨迹是一条复杂的空间曲线,建模较为困难[3]。而对支腿建立的数学模型主要是为了得到水平倾角α、β与各液压支腿位移△Z之间的函数关系,因此借助微分思想将平台的空间运动进行离散,可在相对坐标系内建立比较准确的数学模型。
载重平台系统的调平过程依据可以由平台上的两条相交直线达到水平状态来确定。为了安装与测量方便,可将倾角传感器分别安装在X轴与Y轴上,用来测量这两个方向上的角度信号,角度信号经过算法转化,输出实际的位移控制量,由液压缸驱动来使得液压支腿上升或者下降,从而让平台达到水平状态,载重平台的调平方式,从控制的误差类型来说,可以分为基于位置误差控制和基于角度误差控制两类调平方式。
基于角度误差的调平由于存在分别调整α、β角度值这两个阶段,平台水平状态很难通过一次调平就达到要求,需要反复多次进行调整,因此液压支腿总移动距离较大,调平总耗时也比较长。而基于位置误差调平中,由于液压系统存在一定的滞后性,不能及时响应发出的指令,故应避免出现液压支腿下降的动作,综合考虑,采用追逐式朝最高点靠齐的方式进行调平。
二、液压同步控制系统数学模型
常见的四液压缸载重平台,由一阀控一缸的原理[4],建立其系统模型,系统由平台平面,四个液压缸和液压支腿以及相应的附件构成,为了能够直观地描述液压支腿与平台的调平过程,建立系统的坐标系如图2。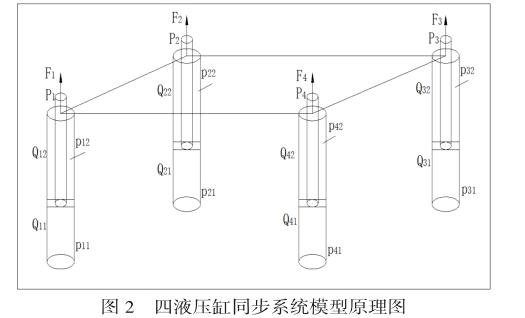
以液压缸1与液压缸4的连线作为系统坐标系的X轴,液压缸1与液压缸2的连线作为系统坐标系的Y轴,Z轴为竖直方向,每个液压缸由单独的比例阀来控制,Qi1、Qi2分別代表阀到液压缸无杆腔与有杆腔的油液流量,Pi1、Pi2分别代表液压缸无杆腔与有杆腔进油口的压力,PiS是电液比例阀进口压力,QiS是油源到电液比例阀的油液流量,i=1,2,3,4,pp是油源处油液压力,Qp是油源处油液流量。Fi是第i个液压支腿的输出力,Pi(Pix,Piy,Piz)为液压支腿与载重平台铰接的中心点坐标,Si(Six,Siy,Siz)为液压支腿的中心点坐标,M是载重平台的质量。
在载重平台调平的过程中,液压支腿运动轨迹可以由质心OC在竖直方向上的位移ZC,绕x轴的转动的角度θx和绕y轴转动的角度θy来描述,因此,以载重平台为对象,由牛顿第二定律以及刚体转动定律可以求出其运动方程 :
三、液压同步控制系统仿真分析
液压平台调平控制过程中针对液压缸工作模式采用了主从式,将其中一个液压缸的输出设定成为其余液压缸输出跟踪的理想值,可在AMESim软件中建立同步控制系统的仿真模型如下图3所示,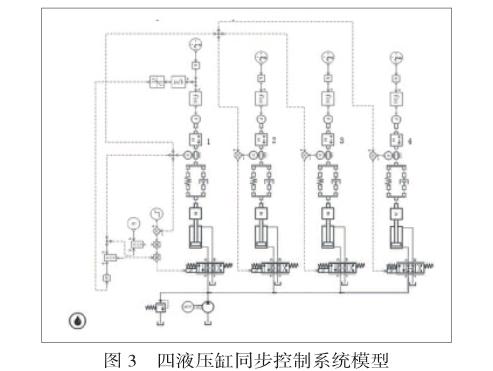
根据数学模型中建立的相应元件,关联一组常见的元件参数,可设置到仿真模型中进行仿真分析,主要元件的仿真参数如表1: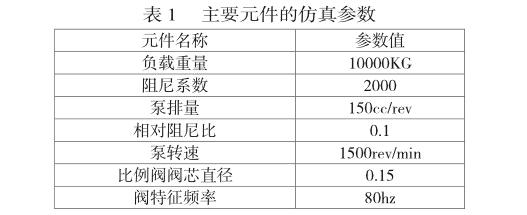
设置4号液压缸支腿为最高位移,对四液压缸调平过程进行仿真,仿真时长设为50s,步长取0.1s。观察四个液压缸的支腿在调平过程中的位移曲线,可得到仿真结果如图4所示。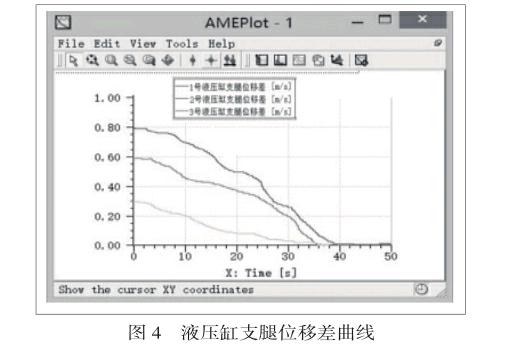
四、结论
由仿真得到的位移曲线可以看出,在支腿调平过程中,处于不同位置的支腿上升速率并不相同,位于最低点的1号液压缸支腿 上升速率最快,2号次之,3号最慢,而位于最高点的4号液压缸支腿,在调平过程中,保持位移不变。
参 考 文 献
[1]凌轩,王旭东,陈赛克.雷达天线车液压升降系统同步控制仿真研究.[J]机床与液压.2013(8):81-83.
[2]仕润霖,冯永保,李淑智,郭晓松.模糊PID控制的车载平台高精度动态调平仿真研究[J]机床与液压.2013(5):150-153.

