找准学习起点 构建有效课堂

杨瑶琴

【摘要】 学生学习起点的把握是否精准，直接影响着课堂教学的效果. 要从自身的教学实践与听课后分析、思考师生今后的发展，明确剖析学习起点的矛盾，找寻有效任务驱动、弹性教学方案、调整教学方案、强化意义建构来把握学习起点，从而构建数学的有效课堂，提高课堂教学的有效性.

【关键词】 小学数学；学习起点；把握；运用；有效课堂

《小学数学课程标准》指出：“数学教学活动必须建立在学生认知发展水平和已有的知识经验基础之上. 由于学生所处的文化环境、家庭背景和自身思维水平不同，学生的数学学习活动应当是一个生动活泼的和富有个性的过程. ”如何把先进的教学理念落实到数学教学实践中来，转化成可操作的教学行为，是我们数学教师必须思考的问题. 尊重学生的生活经验和知识基础，意味着数学教学活动必须把握好学生的学习起点，在学生原有认知水平上组织及展开学习活动. 以下就是笔者对如何有效把握和运用学生学习起点进行的思考与探索.

一、思考：缘于学习起点把握的不容忽视

1. 缘于自身教学实践的思考

在平常的教学实践中，常常出现让人纳闷的现象：同样是经过准备的课，有的课上得顺畅，学生学习积极性高，课堂效率自然就高；而有的课老师讲得累，学生却无精打采，提不起学习的劲头，效果可想而知. 教两个班数学，同样的内容，同样的设计，有时觉得两个班学习情况相差无几，可有时出现的学习效果分析却大不相同. 我想这其中的原因有很多，学生间的个体差异、学习起点的差异是我们不容忽视的.

2. 缘于听课后的分析与思考

我们常常会看到这样的现象：新课刚开始，例题一出示，学生好像就会了，就懂了. 但教师觉得这不是按自己事先已辛辛苦苦地备了的教案流程走，只好生拉硬扯地把学生拉回来，让学生“懂装不懂”. 有时教师认为是一个简单的数学问题，而学生却回答不出. 这其中一个很重要的原因就是教师在预设时对学生的学习起点估计不足. 例如： 一位教师在上二年级数学广角（简单的排列、组合）公开课时，新课一开始就出示三个小朋友排队拍照，问有几种不同的排队方法？接着让学生用三种不同颜色的圆片代表三个小朋友把不同的排队方法摆出来…… 新课教学用了三十多分钟才结束，还有部分同学不是很清晰. 显然，这位教师只是根据自己的理解设计了教学预案，这样的起点对二年级同学来说过高，教师教得累，学生学得也累，且不易接受.

3. 缘于师生今后发展的思考

由于社会迅速发展的信息化与学习化，学生的学习渠道不再仅仅只有教师和教材，他们从父母长辈、课外读物、媒体、网络等多种学习渠道中接受了许多的数学信息. 所以他们的学习准备状态远远超出教师的想象，许多课本上尚未涉及的知识，学生可能已经知道很多了，但这样的学习是不系统的、模糊的、浅层次的. 如果在教学设计时教师还只是把他们当作一张白纸看，或认为他们的起点很高，都会给学生造成学习障碍. 起点过低，学生不感兴趣；起点过高，学生不易接受. 这样都不利于学生的发展.

教师是新课程的实施者，学生的学习起点能否得到有效利用，应取决于教师能否善于寻找和运用学生的学习起点. 作为一线教师的我们要用先进的教学理念武装自己，不断地学习，及时地给自己充电，为我们课堂的有效教学得到保障，也是教师合理寻找、灵活运用学习起点的前提.

看来，只有真正把握好学生的学习起点，才能使我们的教学达到事半功倍的效果，才能让学生们有效发展.

二、明确：基于剖析关于学习起点的矛盾

1. 明确学习起点的概念

“学习起点”是指学生学习新内容所必须具备的知识及能力储备，它可分为学习的逻辑起点与学习的现实起点. 学习的逻辑起点是指学生按照教材学习进度，应该具有的知识、技能积累. 学习的现实起点是指学生在多种学习资源的共同作用下，已经具备的，多于教材所提供的知识、技能积累. 教师对教学环节作出精心预设时，最关键的是要对学生的认知起点进行预测. 这就要求我们教师找准学习的逻辑起点和现实起点，为学生设置最佳的学习起点，促使学生进行有效的学习.

2. 剖析学习起点的矛盾

矛盾一：寻找学习起点 说容易做较难

每名学生的生活、学习环境不同，所接触的人和事物也不尽相同，从而他们的知识水平和生活经验也不完全相同. 因此，要想了解学生的学习起点是件很不容易的事. 进行调查是一种有效的办法. 调查的方式主要有：问卷调查、抽样调查、谈话交流、作业分析等. 可是在一线任教的教师都知道，这是说得容易做得难的事情. 比如说问卷调查、抽样调查，每天都要备课、上课、改作业，基本是没时间进行这两样调查，如果说偶尔为之，还有可能. 因此，平常教学中，经常用到的方式有课前的谈话交流、课后的作业分析等，有经验的老师往往还是凭以往教学中的经验积累为依据.

矛盾二：运用学习起点 时间少反应快

课前预设中，寻找学生学习起点，教师要根据学生的现实知识水平和生活经验进行预设. 在课堂中要随时随地关注学生、了解学生，从学生的情感、态度、知识、技能等方面准确把握学生现实学习水平. 课开始可以先让学生说说你已经知道了什么. 让他们充分展示已有的知识状况. 这种知识的展现是学生对自身学习进行再思考的过程，也可以拉近师生之间的距离，同时也使教师充分了解学生学习的现实起点，以便及时调整自己的教学方式和流程. 同时还可以让学生说说你还想知道什么，方便教师找到学生的最近发展区. 这时教师要善于倾听，善于发现学生回答中有效而实在的、充满童趣的问题. 并通过及时捕捉反馈的信息，了解学生的学习起点，再通过对信息的处理来做问题的调整、教学环节的重组等，使课堂教学有序、有效. 可一堂课的教学时间有限，教师在这过程中既要找到学生的学习起点，又要对学习起点快速作出准确、有效的反应，这对教师的要求很高.

从以上的矛盾中，我们可以看到找寻学生的学习起点不容易，要用好学习起点同样不是易事.

三、实践：探寻学习起点寻找结合的方法

全面了解学生的学习起点，主要是为什么服务呢？学习起点的准确把握，可以使我们准确地定位教学目标，合理地设计教学流程和选择教学方式，才能引导学生进行有效的数学学习活动. 那如何将寻找到的学习起点和运用学生的学习起点有效结合呢？

方法一：有效任务驱动

所谓“任务驱动”就是在学习过程中，学生在教师的帮助下，紧紧围绕一个共同的任务活动中心，在强烈的问题动机的驱动下，通过对学习资源的积极主动应用，进行自主探索和互动协作的学习. 它要求“任务”的目标性和教学情境的创建，使学生带着真实的任务在探索中学习. 如：教学四年级“平行四边形和梯形的认识”时，在课开始回顾了用三角板检验两条直线互相平行关系后，可以布置这样一个任务：如果在这组平行线上再画2条直线，你能组成一个四边形吗？（在学具纸上画一画，画出尽可能多的各种形状的四边形. 说说你画上了怎样的两条直线，围成了怎样的四边形？）

学生的现实起点一定是存在差异的，但在这样一个任务驱动下，每名学生都在积极思考，教师了解到的情况比较真实、全面. 同时通过反馈同学们互相补充、互相学习，其实教师在这过程已有效地将学习起点寻用结合了.

方法二：弹性教学方案

综合学生的逻辑起点和现实起点，我们应对部分教学内容进行适度的调整，对课堂教学进行预设，形成“着眼于整体，立足于个体，致力于主体”综合的、富有弹性的教学方案. 设计时重在大环节的关联式策划，使学习材料具有较强的思考性.

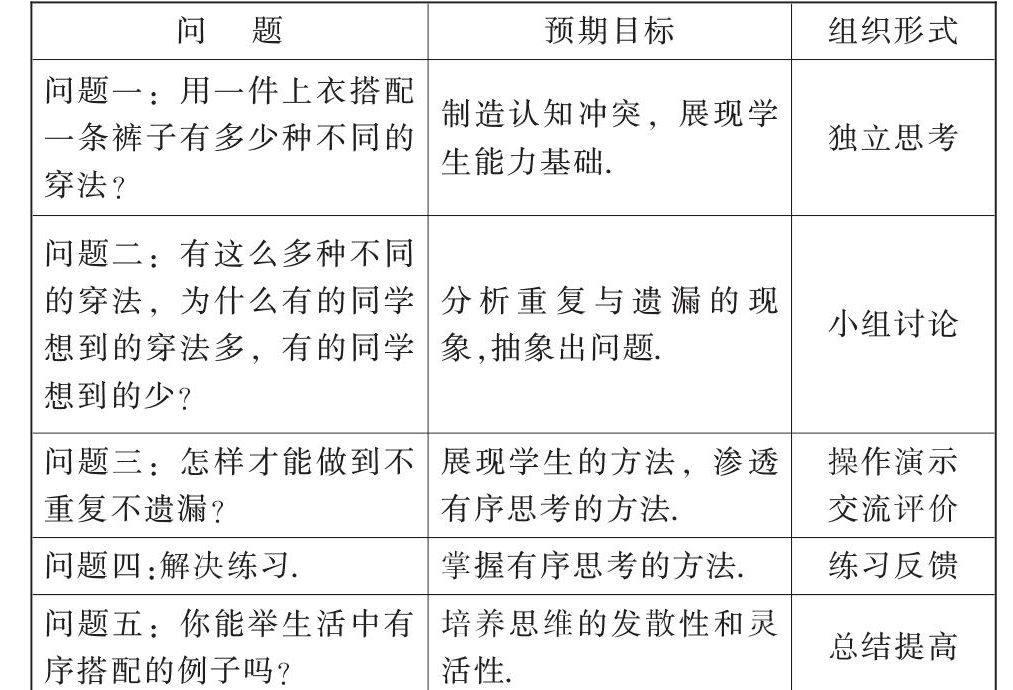
例如：教学三年级上册“数学广角”时，我们可以设计以下弹性教学方案.

在教学方案预设时，教师把本堂课的教学分为这样五个问题，即五个粗的教学环节，每个教学环节之间互相关联，但又存在着弹性空间，教师可以根据教学时的现实情况适度伸缩，达到学习起点的寻用结合，因为课堂教学是一个动态的复杂的过程.

方法三：调整教学方案

苏霍姆林斯基说过：“教育的技巧并不在于能预见到课堂上发生的所有细节，而在于教师根据具体情况，巧妙地在学生中作出相应的变动. ”在教学过程中我们常常会遇到很多课前没有预想到的“可能”，寻找到的学生的学习起点和预设中的情况有所偏差，这时教师就不能死搬硬套教材中的学习材料，不能按照自己事先预设好的方案进行教学，而必须在学生已有的学习经验或提供的学习资源的基础上加工教材所提供的材料，调整自己的预设方案.

例如：一位教师在教学“圆锥的体积”一课时，教师按照教学预设先复习了圆柱的体积的计算方法，并问：有没有好办法能够知道圆锥的体积？

生1：把圆锥浸没在水中，测出水面升高的体积就等于圆锥的体积. （学习迁移）

生2：可以把圆锥铸造成圆柱、长方体或正方体等已学过的立体求体积. （转化思想）

生3：可以用公式进行计算. （教师板书计算公式）

师：对于这个公式，有什么疑问吗？

师：有什么办法可以进行验证一下吗？

师：好，下面我们就来验证一下看，是不是像刚才这名同学所说的，圆锥的体积是否是等底等高的圆柱体积的三分之一？

生：实验用水倒，用沙倒……

以上案例中，这位教师非常关注学生反馈的信息，并能根据学生所反馈的信息，找准了学生的学习起点，从而调整自己的教学方案. 当学生说到可以用公式计算圆锥的体积时，可能已超乎老师的意料之外了，而老师并没有回避学生的问题，是以学生的回答作为一个教学切入点，及时调整了事先设计的教学方案，让学生从验证的角度去进行学习和活动，从而完成教学目标. 正如著名教育家罗伯特所提出的“为学生设计教学”. 这样，既满足了学生表现自己的愿望，还在不知不觉中深化了已有知识，并达到了课堂教学的有效性.

方法四：强化意义建构

在课堂教学中我们还经常组织学生对学习内容进行交流，这时教师要认真观察学生的动作，专心倾听学生的表述，在适当的时候追问，还要关注学生之间的争论，通过及时捕捉信息，了解学习起点，再通过对信息的处理来强化数学知识的意义建构过程，促进知识的理解和内化.

例如：在学习“方程的意义”一课中，学生认识了什么是等式、什么是方程后，安排的教学内容是明确等式和方程间的关系，把结论强加于他们，肯定不行. 怎样让他们在现有的基础上，自主建构知识，发现等式和方程的关系呢？于是我安排了一道练习小游戏，判断下面的式子哪些是等式，哪些是方程. 是等式的男生举手，是方程的女生举手.

师出示第一题：36 - 7 = 29. （男生迅速地举手，女生无人举手）

师出示第二题：60 + x > 70.（在经过一阵短暂的杂乱后，无人举手）我问了缘由，这一题两边不相等，所以既不是等式也不是方程，刚才是因为没看清楚符号.

师出示第三题：6 + x = 14.（女生迅速举手，男生两人举手，其余男生有的观望别人，有的在偷笑，看到这种情况，刚才举手的其中一位男生觉得错了，连忙把手放下）只听见举手的那位男生自言自语：这是等式. （语气坚定）这时又有一位男生也同意这是等式. 于是我顺势引导，你们都同意这是方程吗？（同意）你们同意这是等式吗？（意见不一致）把你的意见和同桌交流一下，再通过全班交流，使学生自主揭示了等式和方程的关系，从而深刻理解了是方程的一定是等式，是等式的不一定是方程的内涵.

试想如果一开始教师不关注学生的现实起点，直接教给学生这两句话，收到的教学效果一定会差很多. 在课堂中再现学生已有的知识、经验，使学习活动成为学生学习经验的总结和升华，从而在理解和内化知识的基础上，实现意义建构.

方法五：抓好教学反思

教学反思是提高课堂教学质量的有效途径，是教师专业成长的催化剂. 课堂中教师必须时刻反思课堂生成的处理、学生的状态，以及每个环节的处理. 如在教学“组合图形的面积”时，让学生自主探究如何使组合图形分解成已学过的基本图形的过程中，从中找出学生的学习起点. 课后反思教学效果如何、师生得到了哪些方面的发展、课堂教学不足和败笔等. 这样使教学经验理性化，可以更好地指导和改进后继教学，从而提高教师运用学习起点的意识.

综上所述，学习起点的把握和应用是小学数学教师的一项基本教学技能，只有真正做到关注与了解每一名学生，精心地进行预案设计，并在教学过程中，随时了解学生反馈信息，及时进行分析判断，大胆进行教学调整，使学习起点的寻找和运用有机结合，才能让我们的数学课堂更加充满活力，师生间的配合更加默契，课堂更有效.

【参考文献】

[1]教育部基础教育司组织编写.走进新课程[M].北京：北京师范大学出版社.

[2]刘福喜，朱桂琴.教师的新视野[M].天津：天津教育出版社.

[3]苏霍姆林斯基.给教师的建议[M].北京：教育科学出版社，2000.

[4]张奠宙.中国数学双基教学[M].上海：上海教育出版社，2006.

[5]唐彩斌.思想改变课堂[M].上海：上海教育出版社，2008.