双谱主成分分析的滚动轴承智能故障诊断

张锐戈, 谭永红

(1．三明学院机电工程学院， 福建 三明 365004；2．上海师范大学信息与机电工程学院，上海 200234)

引 言

滚动轴承振动信号具有周期重复和调制的特点，表现出明显的非平稳和非高斯特性，不适合用传统的功率谱方法分析。双谱分析能处理非平稳和非高斯随机系列，且理论上能完全抑制高斯噪声，在旋转机械故障诊断中得到了广泛的应用。

双谱故障诊断可以划分成谱图法和智能诊断法。谱图法寻找谱图峰值与不同故障类型之间对应关系，最常用的是切片谱，如水平切片、对角切片和中心频率切片[1～3]；或者是计算切片谱的倒谱[4,5]，将成簇谱线简化为单根谱线后寻找故障频率。也有依据双谱的谱峰频率辨别故障类型、并通过纹理特征来判别故障程度的研究成果报道[6]。此外，基于滚动轴承振动信号模型的双谱理论研究表明三阶累积量中不包含故障频率，而双谱中能发现故障特征频率，是因为实际计算时使用时间平均来代替均值[7]。

双谱智能故障诊断由特征提取和模式识别两个环节构成。特征提取方面，分别使用了双谱二值图[8,9]、切片能量[10]、等分区域能量[11]以及灰度共生矩阵[12]等特征参数；模式识别方面，最近邻模板分类器[8,9]、支持向量机[10]、人工神经网络[11,12]等方法都成功地辨识出不同的故障类型。从查询到的资料来看，当前双谱故障诊断研究都基于固定工况情形，还没有考虑工程实践中常见的载荷变化和转速扰动等因素的影响。

实现工况鲁棒的智能故障诊断，首要任务是获得工况鲁棒的特征参量。研究发现双谱的幅值及分布特性在不同轴承状态时具有较大差异性，在轴承状态相同但工况不同时具有较大的相似性。使用主成分分析(PCA)方法提取特征参数，通过线性变换将双谱投影到低维数据空间[13]，继承了双谱的特性并提取出工况鲁棒的特征向量。故障辨识使用连续型隐马尔可夫模型，其观察向量“可见”和状态“不可见”的特点，与故障辨识时依据特征向量判断内在故障类型的要求吻合；此外，隐马尔可夫模型独有的双随机特性，适合从重复再现性不佳的故障信息中判别轴承状态[14]，能适应载荷及转速波动引起的特征参量扰动。

1 滚动轴承振动信号双谱分析

1.1 双谱定义和估计

随机序列s(n)，其双谱定义为三阶累积量的二维傅立叶变换

(1)

式中C3(τ1,τ2)为s(n)的三阶累积量。实际计算时使用有限长度的观察序列，用直接或间接方法估计双谱[15]。

1.2 滚动轴承振动信号双谱特性

轴承振动经过一定的传输路径后才能到达传感器位置。轴承状态不同，其振动激励的位置也不相同，振动传输路径也不一致。因此，振动信号因轴承状态而异，导致双谱幅值和分布特性存在差异，不同轴承状态双谱如图1(a)，(b)，(c)，(d)所示(零载荷，0.177 8 mm故障点直径)。

若轴承状态相同但工况(载荷、转速)不同，可看成是振动激励的位置和传输路径相同，但激励强度和激励频率存在扰动，此时双谱存在一定的相似性。0.177 8mm滚动体故障在4种工况下的双谱如图1(b)和图2(a)，(b)，(c)所示。

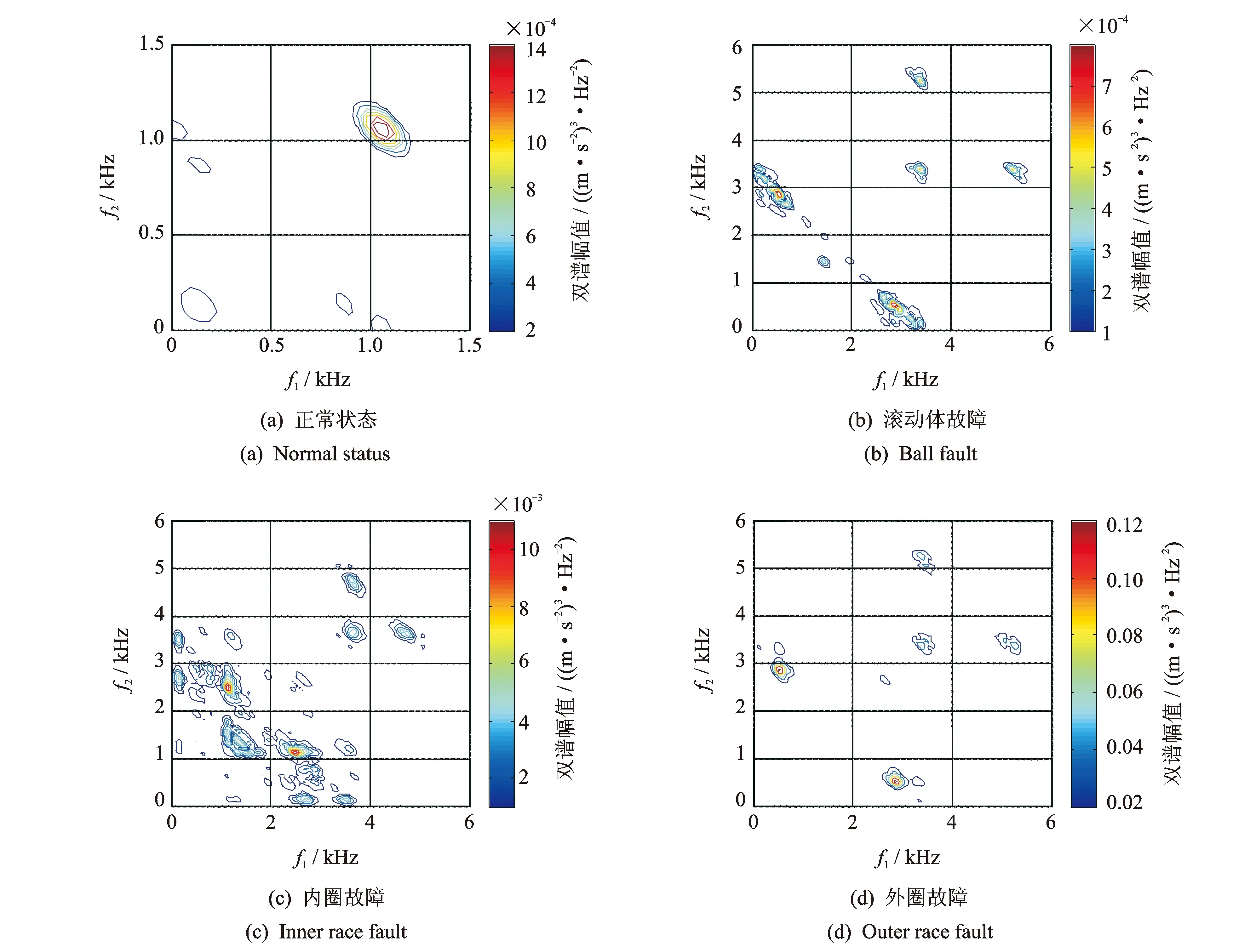
图1 不同轴承状态双谱

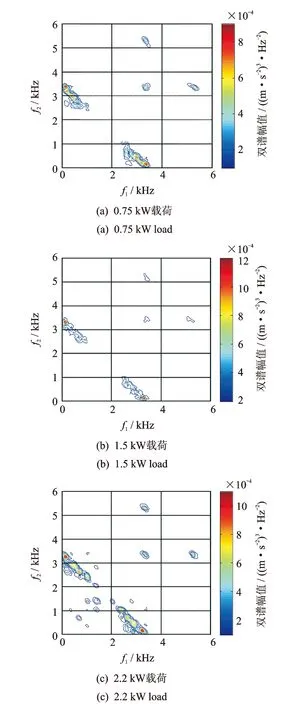
图2 不同工况的滚动体故障双谱

双谱的上述特性，适合用模式识别方法判别不同的轴承状态，也为工况鲁棒故障诊断研究提供了相应的途径。

2 基于PCA的特征向量提取

主成分分析是统计降维方法，通过保留方差较大的主成分而忽略其他成分，在损失较少信息的前提下大幅度地降低数据维数。

双谱幅值可看成是一个L×L维的向量，记为X=[x1,x2,…,xL]，其中xl(l=1,2,…,L)为第l个切片谱的幅值向量。向量X的协方差矩阵定义为

(2)

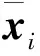
RX=UΣUT

(3)

式中Σ为一对角阵，其元素称为协方差矩阵RX的特征值。特征矩阵U的每一列与Σ中相应列的特征值对应，称为RX的一个特征向量。

从Σ中选择K个较大的特征值，再从U中选出与其相对应的特征向量，并将特征向量依特征值的降序排列，构成变换矩阵Φ为

Φ=[Φ1,Φ2,…,Φk]

(4)

式中Φk(k=1,2,…,K)为第k个特征值对应的特征向量，Φ为L×K维的矩阵。

借助变换矩阵Φ，将L×L维的双谱幅值向量X映射成K×L维的主成分向量Xp为

Xp=ΦTX

(5)

主成分分析通过线性变换将数据映射到低维空间，获得的主成分向量Xp能继承双谱的原有特性，提取到工况鲁棒的特征向量。

主成分数目K依特征值累积贡献率确定[16]

(6)

式中λi为第i个特征值，通过预先设定的Pk值确定需要选择的特征值个数。

3 基于连续型隐马尔可夫模型的故障辨识

对双谱主成分向量Xp各元素取模，得到观察向量O，其构成元素称为隐马尔可夫模型的观察符号。依聚类原理将观察符号分成多个类别，每一类别代表隐马尔可夫模型的一个状态，多个状态构成状态集S为

S={S1,S2,…,SN}

(7)

式中N为状态个数。模型初始时刻，状态特性用初始概率分布矩阵表征

π=[π1,π2,…,πN]

(8)

元素πi表示状态的初始分布概率，定义为

(9)

模型状态随观察向量的变化而发生改变，其过程用状态转移概率矩阵表征

(10)

式中aij表示从状态i转移到状态j的概率，定义为

aij=P(qt=Sj|qt-1=Si),

(11)

式中qt表示t时刻的状态。

转移概率aij不能直接观察，但能用观察符号概率间接表征。连续型隐马尔可夫模型用高斯混合方法合成观察符号概率

(12)

上式表示观察符号Ot属于状态j的概率。其中cjm为混合权系数，M为混合个数，N个状态的混合权系数构成混合权矩阵C；μ和U分别为混合均值矩阵和混合协方差矩阵，η为一高斯概率密度函数。

隐马尔可夫模型训练使用最大期望算法，依据观察向量进行多次迭代运算并确定最优参数。训练好的隐马尔可夫模型由5组参数表征[17]

λ=(A,π,C,μ,U)

(13)

故障辨识阶段，待辨识的观察向量分别输入不同轴承状态的隐马尔可夫模型并计算似然概率P(O|λ)，取值最大的模型状态被识别为待辨识的轴承状态。

4 实验研究

4.1 实验数据

使用凯斯西储大学轴承研究中心数据，为电机驱动端轴承的振动加速度信号，型号是6205-2RS。用电火花在滚动体、内圈和外圈位置加工点蚀故障，以模拟不同的故障类型。每种故障类型都有3种不同的故障程度，故障点直径分别为0.177 8，0.355 6和0.533 4 mm。

电机分4种工况运行，分别采集不同工况、不同故障程度下的轴承正常状态、滚动体故障、内圈和外圈故障信号。信号采样频率为12 kHz，加速度传感器用磁力吸座安装在轴承正上方(12点钟位置)电机外壳上。

电机4种工况的轴向载荷和转速如表1所示。

表1 电机运行参数

4.2 实验流程及参数设置

4.2.1 故障诊断流程

故障诊断分模型训练和故障辨识两个阶段。模型训练使用Baum-Welch算法[17]，通过迭代运算确定观察向量的5组模型参数值；故障辨识阶段，将状态未知的观察向量输入各诊断模型并计算似然概率，取值最大的模型状态被判别为待诊断的轴承状态。训练数据和辨识数据没有重叠，诊断流程如图3所示。

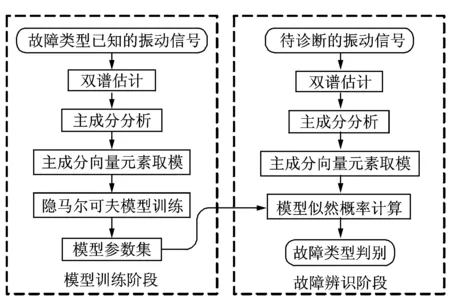
图3 故障诊断流程图

4.2.2 参数设置

实验过程参数设置如下：

(1)双谱：用直接法估计，观察序列长度取1 024个数据点，使用256点数据片段，各片段重复度为75%，频域用宽度为5的Rao-Gabr窗平滑；

(2)主成分分析：特征值累积贡献率Pk常规故障诊断时设为60%，工况鲁棒诊断设为85%，对应的主成分个数为8和16，提取出256×8和256×16维的特征向量；

(3)连续型隐马尔可夫模型：状态和混合个数都设为2，模型初始参数在各自的取值范围内随机赋值，收敛门限值和最大迭代次数分别设为0.001和50。

4.3 实验结果

4.3.1 常规故障诊断

实验分12组进行，每组对应一类故障程度下的一个运行工况。每一种轴承状态，都用1 000个观察向量验证模型诊断效果，正确识别的观察向量数目与输入个数之间的比值称为辨识精度，结果如表2所示。

4.3.2 工况鲁棒故障诊断

工况鲁棒故障诊断使用工况1数据训练的模型来辨识其他3种工况的未知轴承状态，其训练数据和辨识数据之间具有载荷不同和转速波动的特点。实验依故障程度不同分3组进行，每种轴承状态用1 000个特征向量验证辨识精度，结果如表3～5所示。

工况鲁棒故障诊断，虽然使用较多的主成分个数，但辨识精度要比常规故障诊断的低。原因是训练数据与辨识数据来源于不同工况，特征向量受载荷及转速变化的干扰，影响了辨识精度；此外，0.177 8 mm鲁棒诊断的辨识精度优于其他两种故障程度，原因是后者故障点直径较大，产生的振动冲击能量更强，激起的机械振动也更复杂，在特征向量中产生了更大的干扰，导致模型辨识能力下降。

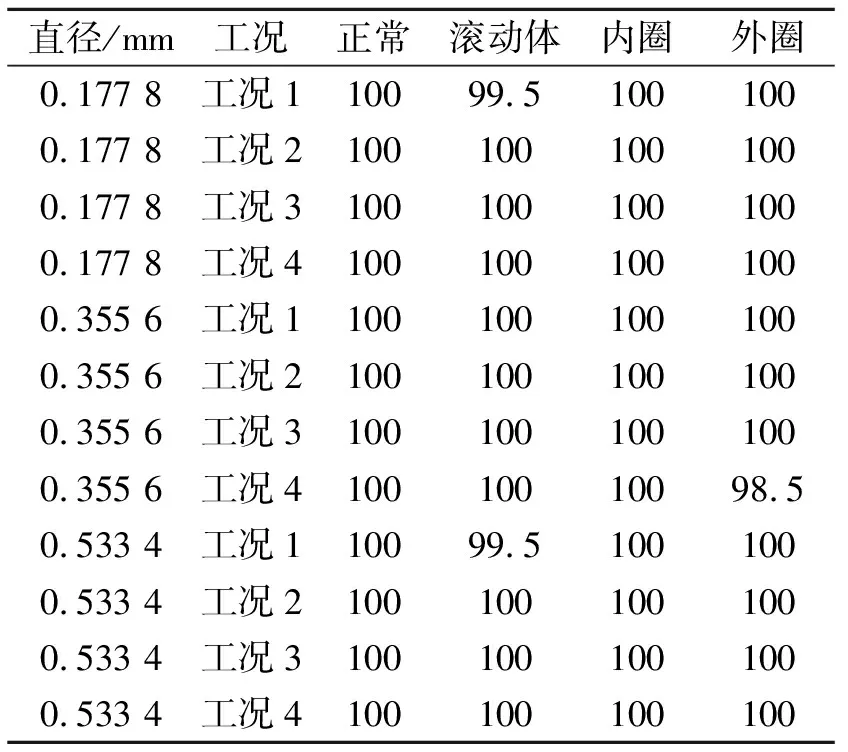
表2 辨识精度/%

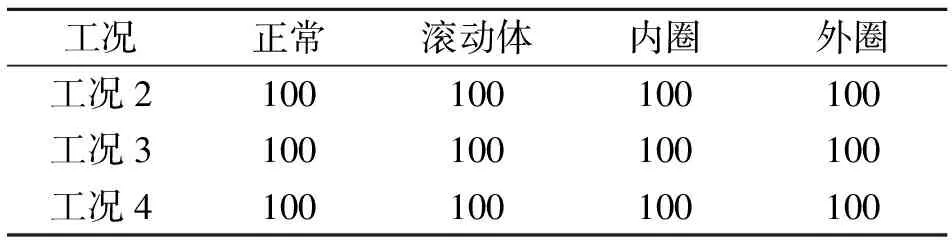
表3 0.177 8 mm鲁棒诊断辨识精度/%

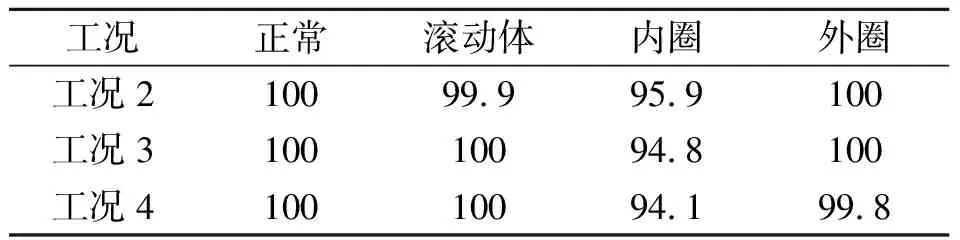
表4 0.355 6 mm鲁棒诊断辨识精度/%

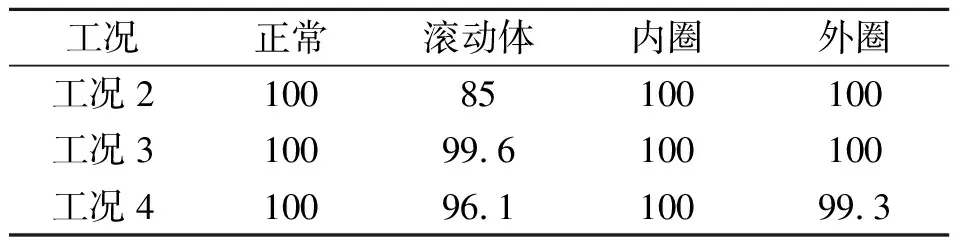
表5 0.533 4 mm鲁棒诊断辨识精度/%

表5中的滚动体故障辨识精度在工况2时明显比其它两种工况的低。从训练数据和辨识数据的双谱差异程度来分析原因。

图4(a)为训练数据双谱，图4(b)，(c)和(d)为3种工况的辨识数据双谱。从幅值来看，工况1，3和4处于同一数量级(标度为10-4)，而工况2差异较大(标度为10-3)；从分布特性来看，工况3和工况1相似度较大，而工况2，4和工况1之间存在一定差异。双谱差异引起特征向量扰动，工况2时受幅值和分布特性双重扰动影响，工况3和工况4幅值扰动较小，且工况3分布特性扰动最小。因而0.533 4 mm故障程度下的鲁棒故障诊断辨识精度在工况2时最低，工况4较高，工况3时最高。

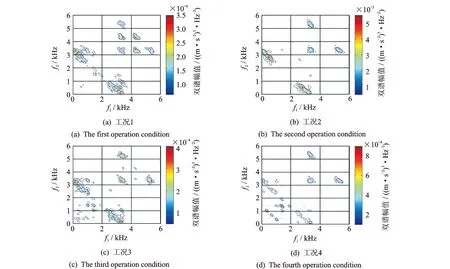
图4 0.533 4 mm滚动体故障在4种工况下的双谱

5 结 论

(1) 双谱能有效表征滚动轴承运行状态信息，在不同故障类型时具有明显差异性，在相同故障但工况不同时具有较高相似性。

(2) PCA能在继承数据原有特性基础上大幅度降低双谱维数，是一种可靠的数据降维方法。

(3) HMM能满足参数扰动情形下的故障辨识，是一种鲁棒的模式识别工具。

(4) 载荷鲁棒故障诊断仅使用工况1数据的模型，任意模型的工况鲁棒故障诊断方法，还有待于进一步研究。

参考文献：

[1] Zhou Y, Chen J, Dong G M, et al. Application of the horizontal slice of cyclic bispectrum in rolling element bearings diagnosis[J]. Mechanical Systems and Signal Processing, 2012, 26: 229—243.

[2] 张琳，黄敏. 基于EMD与切片双谱的轴承故障诊断方法[J]. 北京航空航天大学学报，2010，36(3): 287—290.ZHANG Lin, WANG Min. Fault diagnosis approach for bearing based on EMD and slice bi-spectrum[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(3): 287—290.

[3] 周宇，陈进，董广明，等. 基于循环双谱的滚动轴承故障诊断[J]. 振动与冲击，2012, 31(9): 78—81.ZHOU Yu, CHEN Jin, DONG Guang-ming, et al. Fault diagnosis of rolling element bearing based on cyclic bispectrum[J]. Journal of Vibration and Shock, 2012, 31(9): 78—81.

[4] 李辉，郑海起，潘宏侠. 基于阶次倒双谱分析的滚动轴承故障诊断方法[J]. 中北大学学报(自然科学版)，2008, 29(5): 439—444.LI Hui, ZHENG Hai-qi, PAN Hong-xia. Order bipsectrum based fault diagnosis method for roller bearing[J]. Journal of North University of China( Natural Science Edition), 2008, 29(5): 439—444.

[5] 李辉，郑海起，唐力伟. 基于倒双谱分析的轴承故障诊断研究[J]. 振动、测试与诊断, 2010, 30(4): 353—356.LI Hui, ZHENG Hai-qi, TANG Li-wei. Application of bi-cepstrum technique to bearing fault detection[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(04): 353—356.

[6] 林勇，周晓军，张文斌，等. 基于形态小波理论和双谱分析的滚动轴承故障诊断[J]. 浙江大学学报(工学版), 2010, 44(3): 432—439.LIN Yong, ZHOU Xiao-jun, ZHANG Wen-bin, et al. Rolling bearing fault diagnosis based on morphological wavelet theory and bi-spectrum analysis[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(3): 432—439.

[7] Hernández Montero F E, Caveda Medina O. The application of bispectrum on diagnosis of rolling element bearings: A theoretical approach[J]. Mechanical Systems and Signal Processing, 2008, 22(3): 588—596.

[8] 李学军，蒋玲莉，杨大炼，等. 基于双谱分布区域的齿轮聚类分析与故障诊断[J]. 振动工程学报, 2011, 24(3): 304—308.LI Xue-jun, JIANG LING-li, YANG Da-lian, et al. Cluster analysis and fault diagnosis for gear based on bispectrum distribution[J]. Journal of Vibration Engineering, 2011, 24(3): 304—308.

[9] Jiang L, Liu Y, Li X, et al. Using bispectral distribution as a feature for rotating machinery fault diagnosis[J]. Measurement, 2011, 44(7): 1 284—1 292.

[10] 李凌均，韩捷，李朋勇，等. 基于矢双谱的智能故障诊断方法[J]. 机械工程学报, 2011, 47(11): 64—68.LI Ling-jun, HAN Jie, LI Peng-yong, et al. Intelligent fault diagnosis method based on vector-bispectrum[J]. Journal of Mechanical Engineering, 2011, 47(11): 64—68.

[11] 黄晋英，潘宏侠，毕世华，等. 基于高阶累量谱的轴承故障诊断[J]. 火炮发射与控制学报, 2007(2): 56—59.HUANG Jin-ying, PAN Hong-xia, BI Shi-hua, et al. Bearing fault diagnosis based on high-order cumulant spectrum[J]. Journal of Gun Launch & Control, 2007, (2): 56—59.

[12] 林勇，胡夏夏，朱根兴，等. 基于振动谱图像识别的智能故障诊断[J]. 振动、测试与诊断, 2010, 30(2): 175—180.LIN Yong, HU Xia-xia, ZHU Gen-xing, et al. Intelligent fault diagnosis using image recognition of vibration spectrogram[J]. Journal of Vibration Measurement & Diagnosis, 2010, 30(2): 175—180.

[13] Park M S, Choi J Y. Theoretical analysis on feature extraction capability of class-augmented PCA[J]. Pattern Recognition, 2009, 42(11): 2 353—2 362.

[14] 张锐戈，谭永红. 基于最优Morlet小波和隐马尔可夫模型的轴承故障诊断[J]. 振动与冲击, 2012, 31(12): 5—8.ZHANG Rui-ge, TAN Yong-hong. Fault diagnosis of rolling element bearings based on optimal Morlet wavelet and hidden Markov models[J]. Journal of Vibration and Shock, 2012, 31(12): 5—8.

[15] Yang D M, Stronach A F, Macconnell P, et al. Third-order spectral techniques for the diagnosis of motor bearing condition using artificial neural netwroks[J]. Mechanical Systems and Signal Processing, 2002, 16(2/3): 391—411.

[16] He Q, Yan R, Kong F, et al. Machine condition monitoring using principal component representations[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 446—466.

[17] Rabiner L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Readings in Speech Recognition, 1990, 53(3): 267—296.