刚柔耦合多体系统动力学模型降阶

孙东阳， 陈国平

(南京航空航天大学机械结构力学及控制国家重点实验室， 江苏 南京 210016)

引 言

随着空间技术的发展，航天器柔性构件的尺寸越来越大，柔性构件的变形对航天器的动力学行为产生很大的影响，传统多刚体系统动力学理论已经不能满足人们对设备精度的要求。最近几十年，考虑构件柔性的柔性多体系统动力学，已经成为国内外众多学者研究的热点并取得了大量的研究成果。考虑构件弹性变形与大范围刚体运动的耦合，Likins提出了浮动坐标方法[1]，该方法将构件的位形认为是浮动坐标系大范围刚体运动与相对于该局部坐标系的变形的叠加。1987年，Kane在研究梁的高速旋转运动时第一次发现了动力刚化现象[2]。为解决动力刚化问题，Haering等在多体系统动力学建模过程中考虑了高阶项[3,4]。

然而，浮动节点坐标法是基于小变形假设，对于存在大变形的多体系统已经不再适用。Shabana提出了目前广泛应用于分析大变形柔性多体系统动力学的绝对节点坐标方法(ANCF)[5]。该方法中单元节点的坐标定义在全局坐标系下, 采用斜率矢量代替传统有限单元中的节点转角坐标，推导建立的多体系统微分-代数方程的质量矩阵为常数矩阵，且具有不存在科氏力和离心力项的优点。Berzeri等提出了几种基于不同假设的一维梁的弹性力简化模型[6]，并做了比较研究。Escalona等首先将该单元应用于柔性大变形多体系统动力学的研究[7]。Omar等放宽梁中线的切线矢量与梁截面的法线方向重合的的假设[8]，将梁的剪切变形考虑到梁单元中,首次提出了一种平面应变剪变梁单元。该单元由于弯曲应变与轴向应变不一致而带来剪变闭锁问题。为了解决剪变闭锁问题，Kerkkänen等通过改变单元的运动学描述[9,10],提出了一些可有效减轻剪变闭锁问题的线性剪变梁单元。考虑到绝对节点坐标体系下刚度矩阵的强非线性，导致采用绝对坐标方法建立的微分-代数方程的计算效率比较低, García-Vallejo提出不变矩阵法[11], 该方法将非线性刚度矩阵分解为常数刚度矩阵与广义坐标相关的刚度矩阵之和。

绝对节点坐标法虽然能够精确描述多体系统的刚性运动，但是即使是刚体也要划分单元[12]，这必然导致该方法较难处理刚柔耦合多体系统动力学问题。Sugiyama等结合浮动节点坐标法能有效处理刚体运动和绝对节点坐标法能描述柔性体大变形的特点[13～15]，使存在柔性体大变形的刚柔耦合多体系统得到了解决。然而，浮动节点坐标法建立的多体系统动力学方程的质量矩阵与广义坐标相关，因而得到的刚柔耦合多体系统的微分-代数方程的质量矩阵也与广义坐标相关，每次计算都需要对质量阵进行计算，会大大降低计算效率。自然坐标法以其具有建立的多体系统微分-代数方程的质量矩阵为常数矩阵的优点而成为刚柔耦合多体系统中替代浮动节点坐标法用于描述刚体构件的方法。García-Vallejo用自然坐标法与绝对节点坐标法的混合方法对平面刚柔耦合多体系统动力学进行了研究[16]，并且对构件的各种连接情况进行了讨论。在此基础上，García-Vallejo进一步对空间刚柔耦合多体系统动力学问题进行了研究[17]。

上述研究随着柔性体单元数量的增加，刚柔耦合多体系统动力学方程的计算效率将会比较低。为了提高计算效率，需要对绝对节点坐标法建立的柔性多体系统进行模型降阶。传统的模型降阶方法主要有子结构方法[18～21]，Krylov子空间方法等[22,23]。Hurty首先提出了模态综合法的概念[18]，并且应用于对大规模线性系统进行模型降阶。R R Craig和C C Bampton对此方法作了部分修正[19]，形成了现在的固定界面模态综合法。随后，Kobayashi成功将Craig-Bampton固定界面法应用于基于绝对节点坐标法的柔性多体系统的模型降阶[24]。本文采用Craig-Bampton固定界面法对基于绝对节点坐标法和自然坐标法建立的刚柔耦合多体系统进行模型降价。

1 绝对节点坐标法

1.1 基于绝对节点坐标法的梁单元

绝对节点坐标法中，柔性体k的一维梁单元j，如图1所示，该单元上任意一点全局位置为

rkj=Skjekj

(1)

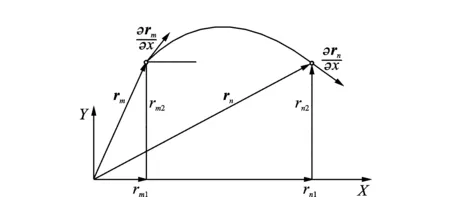
图1 平面梁单元

式中Skj为单元形函数，ekj为单元节点的广义坐标矢量，可表示为

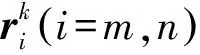
基于上述描述，梁单元的动能可表示为

(2)

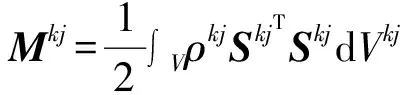
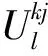
(3)

式中εkj和κkj分别为单元j中线上对应点的应变和曲率。

基于虚功原理，可得到该单元的动力学方程为

(4)

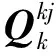
(5)

(6)

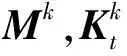
(7)

1.2 模型降阶

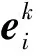
(8)

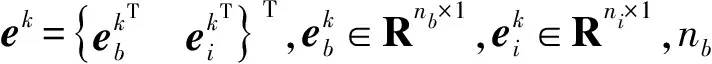
用Craig-Bampton方法进行减缩时，约束模态仅取前nc阶，则广义坐标ek可减缩为

ek=Tkqk

(9)

(10)

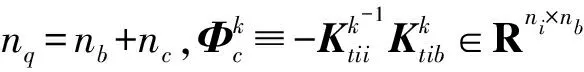
将式(9)代入式(8)，等式两边左乘TkT，则有

(11)

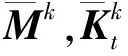
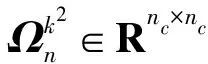
2 自然坐标法

自然坐标法中，用两个基点的绝对坐标矢量描述刚体i的位置和方向，如

(12)

式中di为包含基点C和D的刚体i的坐标矢量(如图2所示)，该坐标矢量是非独立的，C和D之间存在距离约束，有

(13)

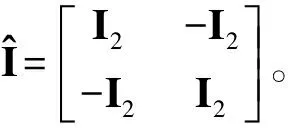
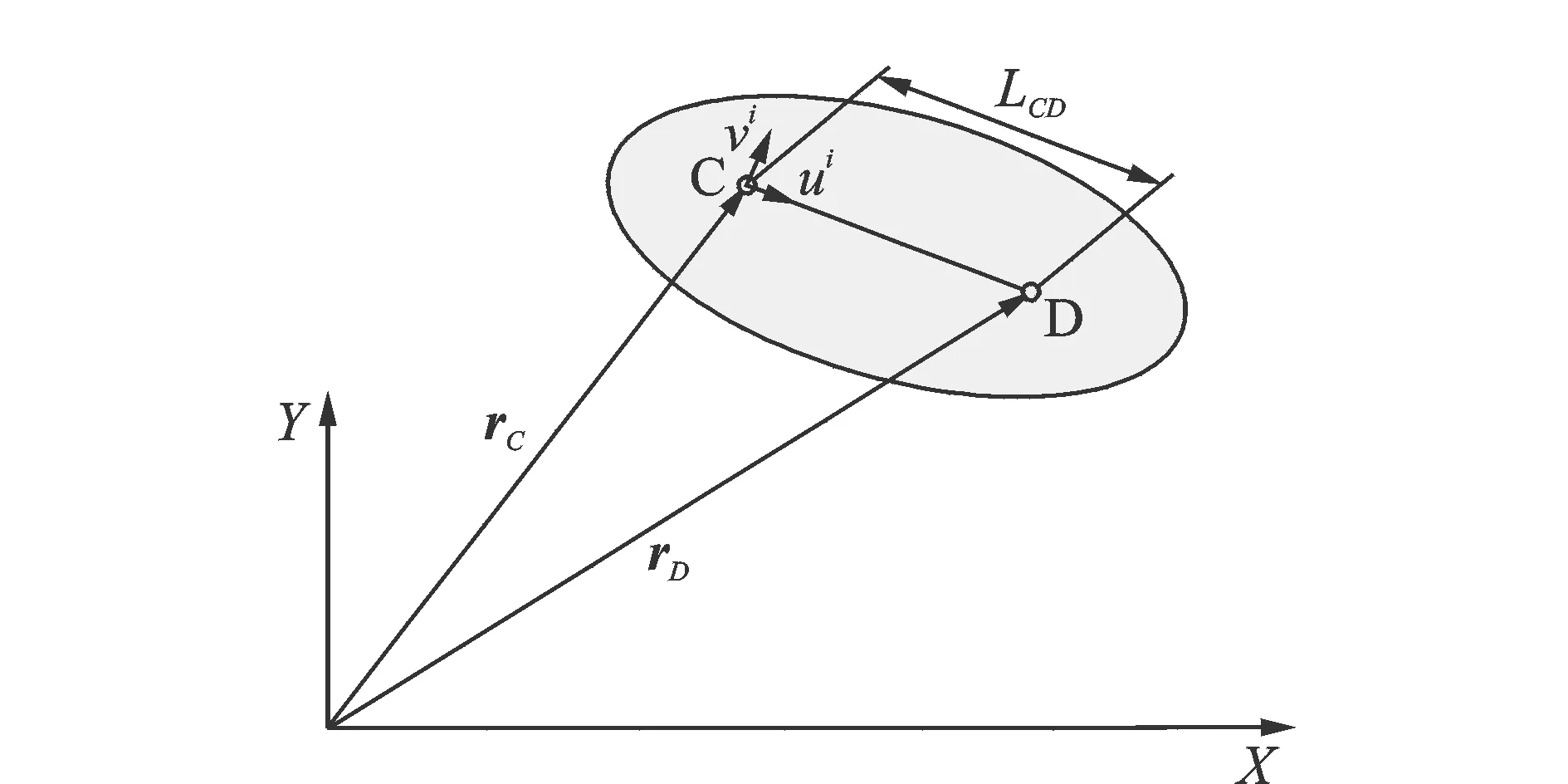
图2 两基点刚体

基于上述刚体描述，自然坐标法建立的刚体系统动力学方程为

(14)

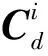
固结在刚体上的动坐标系的旋转矩阵可表示为

(15)

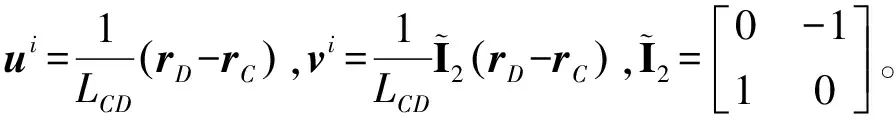
3 刚柔耦合多体系统

柔性体之间、刚体之间、柔性体与刚体之间存在各种约束。本文仅描述刚体与柔性体之间的旋转副约束和固结约束(如图3所示)，其他相关约束可参考文献[16]。

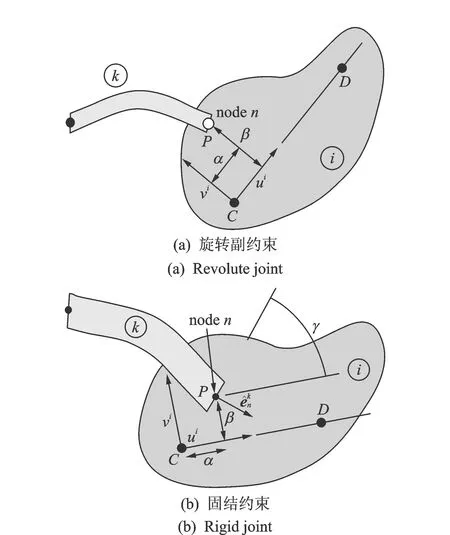
图3 柔性体与刚体之间的约束

3.1 旋转副约束

假设刚体i的P点与柔性体k的节点n存在旋转副约束(如图3(a)所示)，约束方程可表示为

(16)

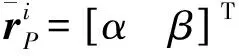
(17)

式中

3.2 固结约束

假设刚体i的P点与柔性体k的节点n存在固结约束(如图3(b)所示)，则约束点除了存在位置约束外还存在方向约束，即

(18)

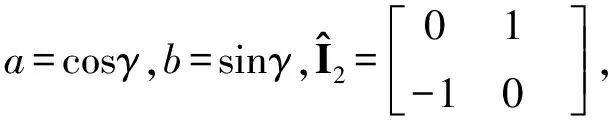
(19)

式中

3.3 消除线性约束方程

将约束节点作为柔性体的边界，则柔性体的边界节点广义坐标可以用连接刚体的自然坐标和柔性体边界的减缩坐标表示。假设刚体i的P点与柔性体k的节点n存在旋转副约束，则柔性体k经Craig-Bampton方法减缩后的广义坐标可表示为

(20)

由式(11)和(14)得刚柔耦合多体系统动力学方程为

(21)

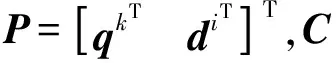
由式(20)可以对广义坐标P进行减缩

(22)

将式(22)代入式(21)，等式两边左乘TT，则

(23)

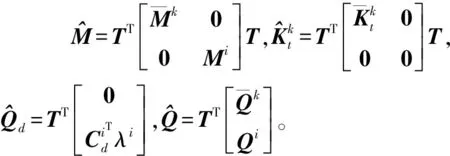
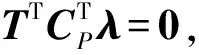
假设刚体i的P点与柔性体k的节点n存在固结约束，同理可得消除边界约束后的刚柔耦合多体系统动力学方程为

(24)

4 数值算例

图4为受重力的平面双摆。相关参数参考文献[25],A点与B点均为旋转铰，梁AB与梁BC的长度均为1.8 m，截面积为2.5×10-4m2，密度为2.766 67×103kg/m3。梁AB与梁BC都可以作为刚体或柔性体。本文首先基于3种情况对该双摆系统进行动力学分析：(1)梁AB与梁BC均为柔性体，用绝对节点坐标法对其进行研究；(2)梁AB与梁BC均为刚体，用自然坐标法对其进行研究(NCF)；(3)梁AB为柔性体，梁BC为刚体，用文献[16]的平面刚柔耦合多体系统动力学方法对其进行研究(NCF-ANCF)。如果梁为柔性体，将梁等分为10个单元，杨氏模量为6.895×109Pa，截面惯量矩为1.302×10-9m4，取重力加速度为9.81 m/s2，仿真时间为2.5 s。在一台具有Intel Pentium 3.2 GHz处理器及3GB RAM的PC机上运行。3种情况下，C点Y方向的绝对位移如图5所示

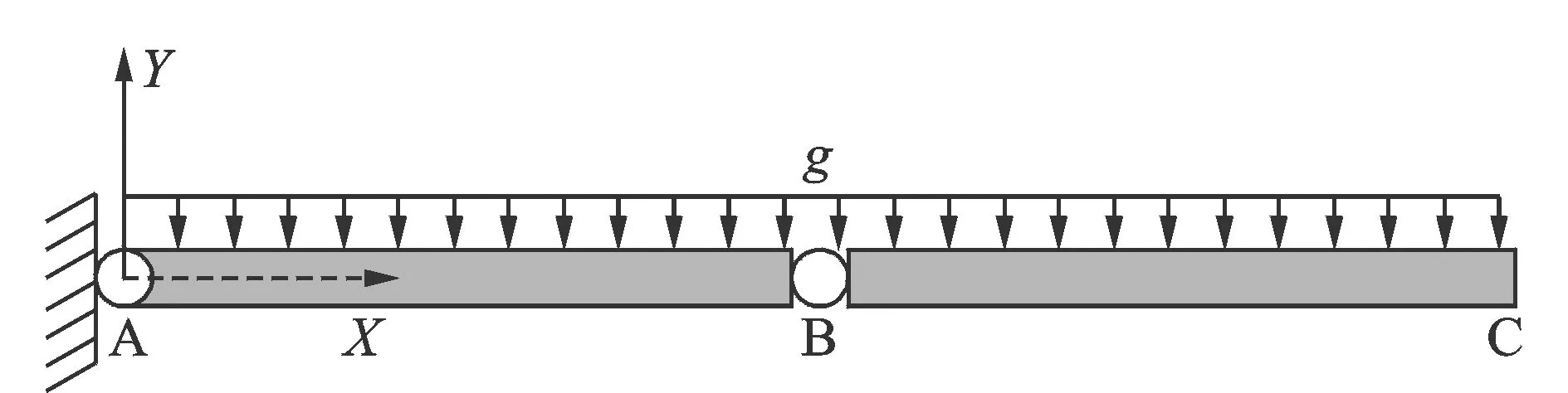
图4 双摆

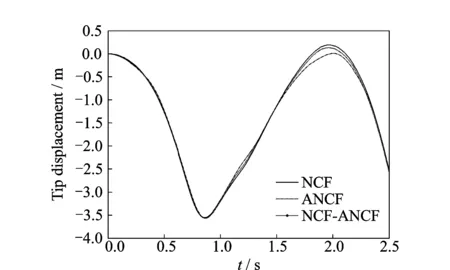
图5 C点Y方向绝对位移

由图5可知，3种情况下C点Y方向的位移存在差异，这说明弹性变形对双摆端点C的运动会产生影响，但3种情况下C点位移相差不大，因此，在精度要求不高的情况下，可以把梁作为刚体考虑。

多体系统按照构件在运行过程中的变形，可以将构件分为刚体构件和柔性体构件，其中，随着柔性体构件划分单元数量的增加，刚柔耦合多体系统动力学方程会存在计算时间长，计算效率低的问题。因此，本文将模型降阶的方法引入刚柔耦合多体系统动力学，提出基于模态综合法的刚柔耦合多体系统减缩方法，解决了传统存在大变形的刚柔耦合多体系统动力学方程计算效率低的问题。为了验证该方法的正确性和有效性，本文以图4的双摆为例，将梁AB作为柔性体，取其杨氏模量为6.895×108Pa，梁BC作为刚体，用该方法对此系统进行研究。在选取主模态集时，分别取前5阶模态(C-N-A(5))，前7阶模态(C-N-A(7))和前9阶模态(C-N-A(9))，将其与原模型(N-A)进行对比。减缩模型和原模型C点Y方向位移和柔性梁端点横向变形分别如图6，7所示,计算所耗CPU时间如表1所示。

表1 计算所耗CPU时间

由图6可知，取较少的主模态就能使C点Y方向绝对位移误差很小，这是因为柔性梁的振动主要为低频振动，因此，只用选取较少的模态就能粗略描述柔性梁的弹性变形。图7中，原模型的柔性梁端点横向变形曲线与取前9阶模态时的柔性梁端点横向变形曲线几乎重合，而与取前5阶、前7阶模态时的柔性梁端点横向变形曲线存在明显差异。由此可见，只有适当选取更多模态才能更好地描述柔性体的弹性变形。由表1可知，减缩模型的计算时间都比原模型的计算时间要少，而且选择的模态数量越少越节省计算时间。结合图7和表1可以得到：减缩模型仅选取前9阶模态时，能够在满足计算精度的情况下使计算时间仅为原模型计算时间的34.9%。由上述分析可知，适当选取模态就可以在保证计算精度的情况下，减少刚柔耦合多体系统动力学方程的计算时间，从而提高计算效率。

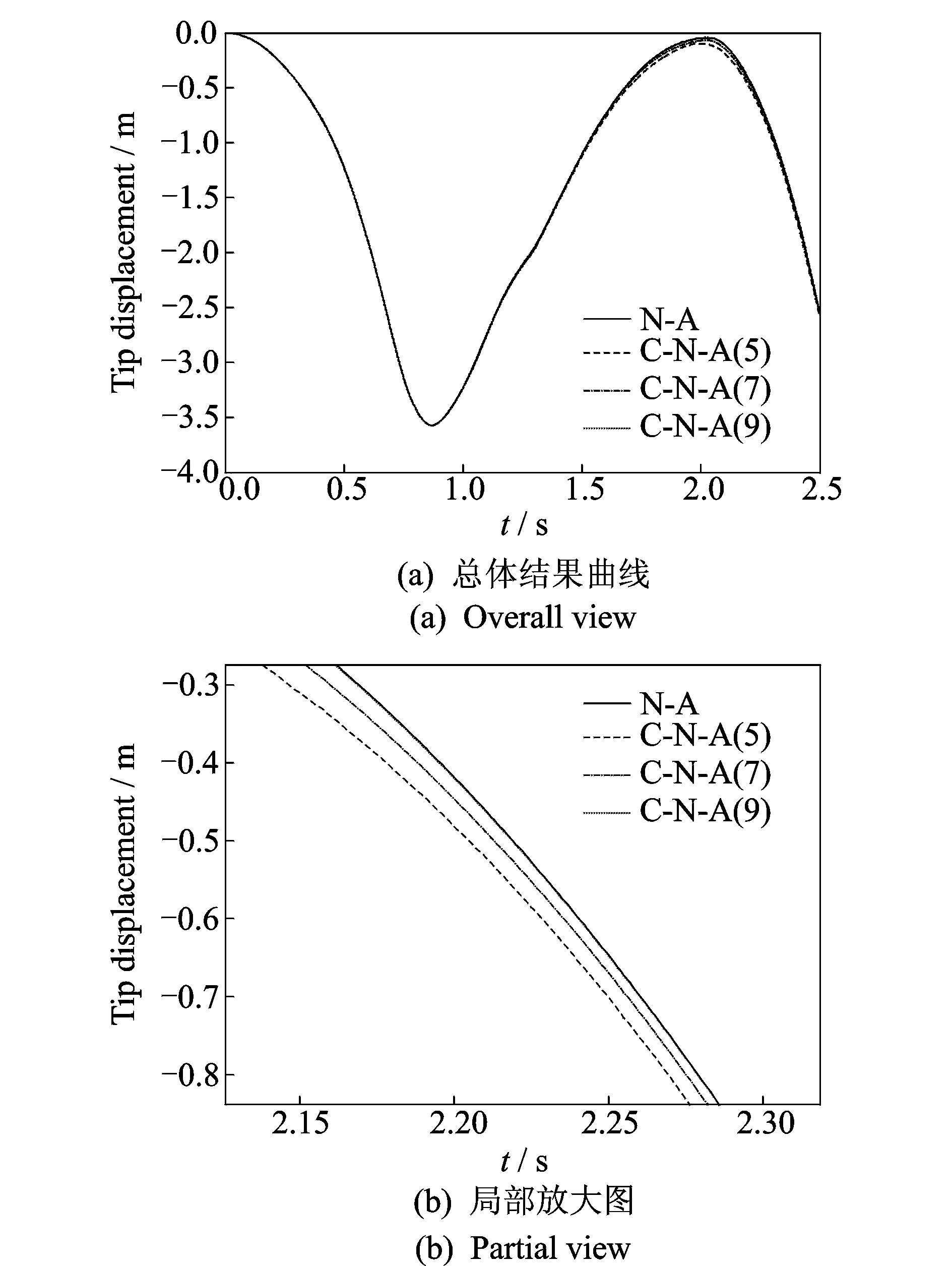
图6 C点Y方向绝对位移

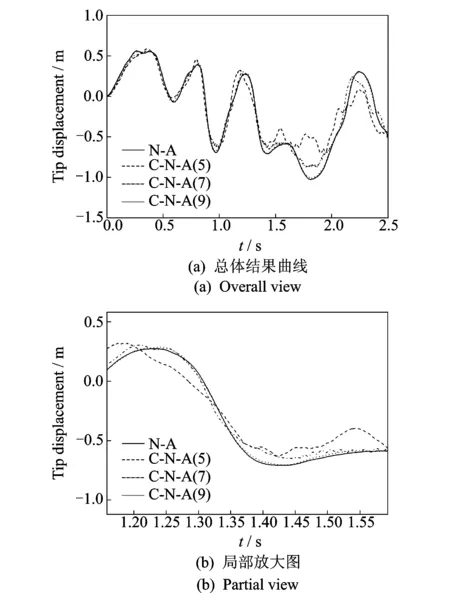
图7 柔性梁端点横向变形

5 结 论

本文考虑到存在大变形的刚柔耦合多体系统动力学方程计算效率比较低，提出了基于模态综合法的刚柔耦合多体系统模型降阶方法。通过双摆系统对该方法的正确性和有效性进行了研究。由数值仿真可知，减缩模型随着选择模态数量的减少，同原模型相比越节省计算时间，而且只要适当选择减缩模态就可以保证计算精度。这说明该方法能够提高刚柔耦合多体系统动力学方程的计算效率。

参考文献：

[1] Likins P W. Finite element appendage equations for hybrid coordinate dynamic analysis[J]. Journal of Solids and Structures, 1972, 8: 709—731.

[2] Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139—151.

[3] Haering W J, Ryan R R, Scott R A. A new flexible body dynamic formulation for beam structures undergoing large overall motion[A]. 33rd Structural Dynamics and Materials Conference[C]. Dallas: AIAA, 19921415-1423.

[4] Mayo J M, García-Vallejo D, Domínguez J. Study of the geometric stiffening effect: comparison of different formulations[J]. Multibody System Dynamics, 2004, 11: 321—341.

[5] Shabana A A. Definition of the slopes and the finite element absolute nodal coordinate formulation[J]. Multibody System Dynamics, 1997, 1: 339—348.

[6] Berzeri M, Shabana A A. Development of simple models for the elastic forces in the absolute nodal coordinate formulation[J]. Journal of Sound and Vibration, 2000, 235(4): 539—565.

[7] Escalona J L, Hussien H A, Shabana A A. Application of the absolute nodal coordinate formulation to multibody system dynamics[J]. Journal of Sound and Vibration, 1998, 214(5): 833—851.

[8] Omar M A, Shabana A A. A two-dimensional shear deformable beam for large rotation and deformation problems[J]. Journal of Sound and Vibration, 2001, 243(3): 565—576.

[9] Kerkkänen K S, Sopanen J T, Mikkola A M. A linear beam finite element based on the absolute nodal coordinate formulation[J]. ASME Journal of Mechanical Design, 2005, 127: 621—630.

[10] García-Vallejo D, Mikkola A M, Escalona J L. A new locking-free shear deformable finite element based on absolute nodal coordinates[J]. Nonlinear Dynamics, 2007, 50: 249—264.

[11] García-Vallejo D, Mayo J, Escalona J L, et al. Efficient evaluation of the elastic forces and the Jacobian in the absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2004, 35: 313—329.

[12] 田强，张青云，陈立平，等. 柔性多体系统动力学绝对节点坐标方法研究进展[J]. 力学进展, 2010, 40(2): 189—202.TIAN Qiang, ZHANG Yunqing, CHEN Liping, et al. Advances in the absolute nodal coordinate method for the flexible multibody dynamics[J]. Advances in Mechanics, 2010, 40(2): 189—202.

[13] Lee S, Park T, Seo J, et al. The development of a sliding joint for very flexible multibody dynamics using absolute nodal coordinate formulation[J]. Multibody System Dynamics, 2008, 20: 223—237.

[14] Hussein B A, Weed D, Shabana A A. Clamped end conditions and cross section deformation in the finite element absolute nodal coordinate formulation[J]. Multibody System Dynamics, 2009, 21: 375—393.

[15] Sugiyama H, Yamashita H. Spatial joint constraints for the absolute nodal coordinate formulation using the non-generalized intermediate coordinates[J]. Multibody System Dynamics, 2011, 26: 15—36.

[16] García-Vallejo D, Escalona J L, Mayo J, et al. Describing rigid-flexible multibody systems using absolute coordinates[J]. Nonlinear Dynamics, 2003, 34: 75—94.

[17] García-Vallejo D, Mayo J, Escalona J L, et al. Three-dimensional formulation of rigid-flexible multibody systems with flexible beam elements [J]. Multibody System Dynamics, 2008, 20: 1—28.

[18] Hurty W C. Dynamic analysis of structural systems using component modes[J]. AIAA Journal, 1965, 3(4): 678—685.

[19] Craig R R, Bampton M C C. Coupling of substructures for dynamic analysis[J]. AIAA Journal, 1968, 6(7): 1 313—1 319.

[20] Hou S N. Review of modal synthesis techniques and a new approach[J]. Shock and Vibration Bulletin, 1969, 40(4): 25—30.

[21] 王文亮，杜作润，陈康元. 模态综合技术短评和一种新的改进[J]. 航空学报, 1979, 3(2): 32—51.

[22] Antoulas A C. Approximation of Large-scale Dynamical Systems[M]. Philadelphia: SIAM, 2004.

[23] Bai Z. Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems[J]. Applied Numerical Mathematics, 2002, 43: 9—44.

[24] Kobayashi N, Wago T, Sugawara Y. Reduction of system matrices of planar beam in ANCF by component mode synthesis method[J]. Multibody System Dynamics, 2011, 26: 265—281.

[25] 李彬. 作大范围空间运动的柔性梁的刚-柔耦合动力学[D]. 上海: 上海交通大学, 2005.Li Bing. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion[D]. Shanghai: Shanghai Jiao Tong University, 2005.