机翼失速颤振抑制的合成射流相位控制方法

张海成， 刘春嵘， 徐道临， 胡 振

(1.湖南大学机械与运载工程学院， 湖南 长沙 410082； 2.湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082)

引 言

近年来，由于高空长航时飞行器(HALE)在军事及民用任务方面的需要，使其研究备受关注。为提高升力并降低诱导阻力及自身重量，这类飞行器多采用大展弦比轻质复合材料机翼，过高的柔性使机翼的气动弹性特性变差，也使颤振这一气动弹性不稳定问题更为突出。为解决飞机轻量化与刚度裕度的矛盾，美国于上世纪90年代开展了主动气动弹性机翼(AAW)技术的飞行试验研究，其设计思想是充分利用机翼的气动弹性效应[1]，并借助主动控制系统驱动控制面，从而优化气动弹性特性。上述技术主要考虑机翼结构问题来进行控制。气动弹性问题是气动力、弹性力和惯性力耦合作用的结果，故也可通过控制流场来抑制颤振。

基于合成射流(Synthetic Jet, SJ)的主动流动控制技术的诞生，为解决上述问题提供了全新的思路和方向。合成射流具有无需额外气源、结构微型化和响应频带宽等优点，并且将合成射流激励器安装于机翼，即可显著改变周围流场分布[2]，因而吸引了国内外研究者的广泛关注。在推迟流动分离、提高升力降低阻力和射流矢量控制等领域[3～5]，合成射流技术已经展现了良好的应用前景，甚至有少数学者开始探索将合成射流技术应用于机翼的颤振抑制。这些有益的研究尝试包括但不局限于如下工作:Marzocca等人基于Theodorsen非定常气动理论[6]，建立了二元机翼气动力及其力矩关于合成射流激励器在弦长位置的拉普拉斯传递函数。运用相位滞后-超前校正环节，合成射流喷射速度对于任一迎角做出相应调整，从而改善系统瞬态响应和稳态精度，达到抑制颤振的目的。随后，他们针对这一问题，又采用滑模控制策略使系统状态按预定的轨迹运动，收束至期望的动态特性[7]。Palaniappan等人则采用LQR线性二次型调节器控制方法[8]，对一线性的二元机翼动力学模型进行颤振抑制。此外，他们还采用CFD软件对NACA0012三元机翼进行了数值仿真，并分析了合成射流激励器的数量对颤振抑制效果的影响。不难看出，以上研究都是基于合成射流可影响气动力和气动力矩这一事实，建立相应的传递函数或状态空间表达式，采用各种闭环控制策略，使系统满足预期的性能指标。但是，将机翼颤振抑制视为控制问题，有赖于对动力学系统有充分的了解，试验验证也必须借助于精密复杂的控制系统及伺服驱动系统，因而存在明显的不足。此外，还需要指出的是，上述研究对象都是经典颤振问题，并未关注失速颤振时涡旋周期性脱落对机翼形成的脉动载荷影响。现代的高空长航时飞行器飞行速度通常在经典颤振的临界颤振速度以内，但是其在穿越对流层等大气活动复杂区域的过程中，活跃的湍流或阵风有可能使其处于大迎角飞行，容易诱发失速颤振。流动分离和涡旋脱落引起的机翼失速颤振通常会造成灾难性的后果。

为抑制大展弦比复合材料机翼的失速颤振, 本文提出基于合成射流的涡脱相位控制方法。建立了复合材料三元机翼的动力学模型，并采用CFD软件数值模拟研究了合成射流相位与涡脱相位之间的关系，证实在一定条件下合成射流可控制涡脱相位。利用合成射流控制翼展涡脱相位减小脉动气动载荷在各阶振型上的投影幅值，可达到抑制机翼失速颤振的目的。以NACA0012翼型为例，数值模拟了合成射流相位控制作用下机翼的气动响应，从而验证合成射流相位控制方案的有效性。

1 计算模型与数值方法

1.1 复合材料三元机翼动力学模型

考虑图1所示的柱形复合材料壳体结构，其长度为L，厚度为h，最大横截面特征长度为c，中面曲率半径为r。建立直角坐标系x,y,z和曲线坐标系x,s,n。其中y轴正向为来流速度V方向；s,n分别为曲线坐标系下切向坐标和法向坐标；坐标y,z及厚度h都是s的函数。假定h≪c,h≪r,c≪L，且不考虑壳体环向应力和横向剪切变形。

考虑到大展弦比机翼的变形特点，忽略轴向变形及水平弯曲变形，将机翼简化为仅有竖向弯曲振动和扭转振动的沉浮-俯仰(Plunge and Pitch)两自由度悬臂梁模型，其中w表示上下运动的位移，向上运动为正向；α为扭转角，抬头为正(顺时针转向为正，如图1所示)。

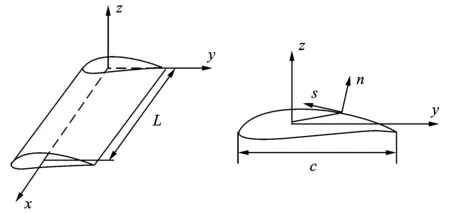
图1 三元机翼模型简图

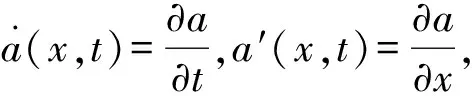
二阶近似位移场可表示为[9]

(1)

式中g(s,x)为修正翘曲函数。因此，二阶近似应变场可表示为

(2)

由于没有内压作用在机翼壳体上，环向应力可忽略不计，所以壳体的应变能密度可写成

(3)

式中A(s),B(s),C(s)分别为缩减轴向、耦合和剪切刚度，且有

(4)

式中Aij(i,j=1,2,6)表示复合材料层合板的面内刚度系数。

因此，壳体应变能可表示为

(5)

其中，运动变量δT可定义为δT={α′,w″}；C2×2为2×2的对称刚度矩阵，其表达式如下

(6)

式中Ae为机翼横截面面积，其计算表达式如下

(7)

考虑到h≪c，c≪L，忽略高阶项的影响，因而动能可表示为

式中ρ是复合材料密度，且有

(9)

1.2 考虑脉动升力的失速气动力模型

已有的研究表明[10]，机翼迎角达到临界失速迎角后，气流粘性和逆压梯度引起边界层分离现象。较大的迎角使涡旋无法附着在翼面上，在机翼的后缘周期性地脱落，从而形成脉动载荷形式的激励力。

为此，将振动机翼的气动力分解为基于格罗斯曼理论的准定常气动力项和涡旋脱落引起的非定常项。机翼的气动升力FL及气动力矩ME可写成

(10)

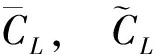
由于本文采用的NACA0012为对称翼型，故零迎角时升力系数和力矩系数均为零。

(11)

式中αe为格罗斯曼准定常气动力模型中的等效迎角，有

(12)

式中a为刚心至弦中点的距离与半弦长的比值(刚心在弦中点后为正)。

(13)

式中AL,AM分别为脉动升力和脉动力矩的幅值；ωe为涡旋周期性脱落的频率；βL,βM分别为初相位。

三元机翼的升力系数可由片条理论得到

(14)

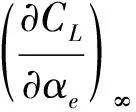
α(x)=α0+φ(x)

(15)

式中α0为翼根的初始迎角，φ(x)为展长x处的扭转角。

因此，气动力做功W可写为

(16)

1.3 运动微分方程及边界条件

根据哈密顿原理

(17)

且由式(15)可知

(18)

将式(5)，(8)及(16)代入式(17)得，运动微分方程为

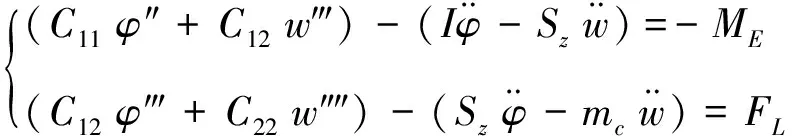
(19)

机翼可简化为悬臂梁，翼根x=0及翼尖x=L处应满足如下条件

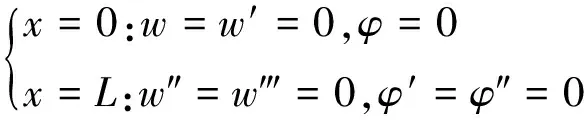
(20)

1.4 数值求解方法

由于式(19)表示的运动控制方程为耦合的偏微分方程组，无法获得其精确的解析解，故需借助数值求解方法对其进行求解，本文采用Galerkin方法对其进行求解。根据Garlerkin法，设式(19)的近似解具有如下形式

(21)

式中Ψj(x)，Φj(x)分别为悬臂梁弯曲振动和扭转振动的振型函数，表示如下

(22)

以振型函数为权函数，并利用其正交性，采用伽辽金方法将偏微分方程转化为如下方程组

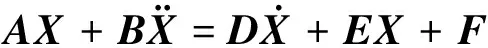
(23)

式中X为机翼的运动位移主坐标;A,B分别为广义结构刚度和广义质量矩阵;D,E分别为广义气动阻尼和广义气动刚度矩阵;F是激励力矩阵。采用MATLAB软件的ODE积分求解器求解方程，即可得到系统的动力学响应。

2 抑制机翼失速颤振的合成射流相位控制方法

2.1 合成射流控制涡脱相位

王晋军等学者通过实验研究发现[11]，合成射流可诱导产生周期性的涡结构，其脱落频率ωs等同于合成射流激励频率ωe。事实上，借助于CFD软件数值模拟也发现，合成射流的激励频率ωe靠近涡脱基频ωs时，激励器的相位差可以反映在对应的涡脱相位上，即通过合成射流可进行涡旋脱落的相位控制，进而控制脉动升力系数和力矩系数的相位。数值模拟的过程可简述为如下：

合成射流的喷射速度矢量U可写为

U=UJsin(2πNJt+θ0)d

(24)

式中NJ为合成射流的喷射频率，UJ为射流速度的幅值，d是喷射速度的方向矢量，θ0则代表合成射流初相位。当涡旋从机翼尾缘交替地脱落时，喷射合成射流将使涡脱的相位有一定程度的延后。表1给出了CFD软件模拟的合成射流初相位θ0与涡脱相位的关系，其中翼型为NACA0012二元机翼，喷射速度幅值UJ为10 m/s，合成射流喷射的方向矢量d与翼型切向夹角为25°时，迎角α为15°，合成射流初相位分别θ0为0°，90°及180°。比较表1所示的三种工况，当合成射流喷射频率接近涡脱基频时，后者相位差仍然保持为90°左右，而对应的涡脱二次谐波相位差则改变为180°左右。表1的结果说明，在三元机翼的翼展上布置若干合成射流激励器，可以控制相应的涡脱相位差。

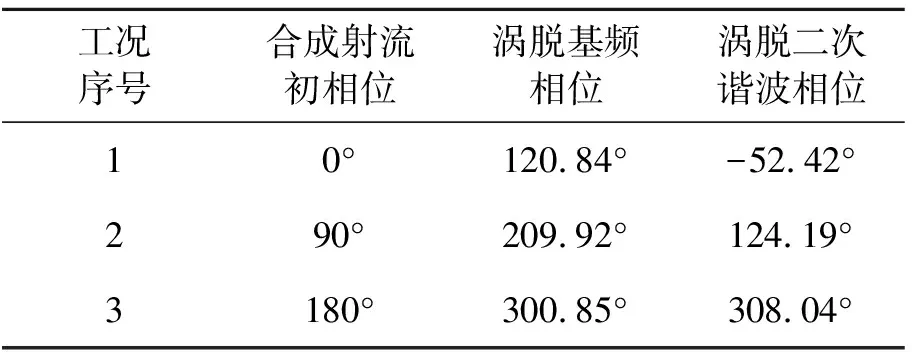
表1 合成射流相位与对应的涡脱相位

2.2 抑制失速颤振的相位控制方法

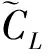
(25)

(26)

式中k为单位长度内的相位角度变化，即波数，Δβ为脉动力矩与脉动升力系数的初相位差，为一常数。式(25)，(26)可写作

(27)

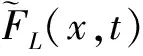
(28)

(29)

波数k增大，意味着翼展方向上脉动气动载荷的波峰与波谷分布更均匀，因而式(27)的定积分值减小，脉动升力在翼展的上下表面附近交替分布相互抵消，有效地降低了激振力幅值，从而降低失速颤振的危害。

2.3 数值验证

采用上文建立的动力学模型，以某NACA0012复合材料三元机翼为例，数值验证相位控制方法抑制失速颤振的效果。机翼壁面为6层斜交对称的复合材料层合板，铺层角为20°，材料为国产碳纤维环氧树脂基复合材料HT8/5288。复合材料特性及机翼结构参数如表2所示。

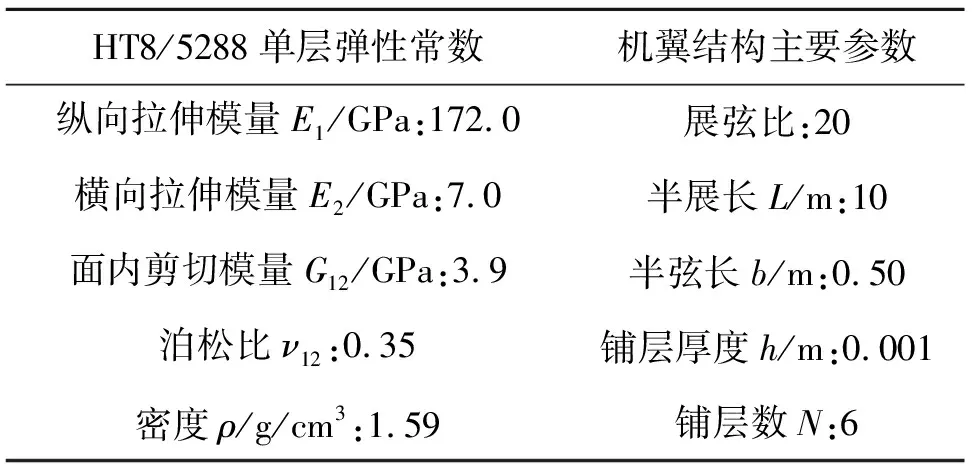
表2 HT8/5288复合材料及NACA0012机翼基本参数

以脉动升力和脉动力矩幅值为单位1，脉动力矩与脉动升力相位差为零为计算工况，通过数值模拟给出机翼前两阶弯曲扭转幅频特性曲线，如图2所示。

图2以幅频特性展示了这一方法抑制失速颤振的效果。可以看出，随着波数k递增，失速颤振的共振峰得到明显削弱：波数k=15时，与未施加合成射流的最大振幅相比，一阶弯曲和一阶扭转的共振幅值分别被降低到5.09%(激励频率3 rad/s左右)和6.75%(激励频率165 rad/s左右)；而二阶弯曲和二阶扭转的共振幅值也分别被降低到3.49%(激励频率64 rad/s左右)和11.1%(激励频率492 rad/s左右)。注意到，合成射流相位控制抑制机翼的失速颤振既不需要复杂的控制律及液压伺服系统，也不需要系统动力学参数的全部信息，因而更简单易行。

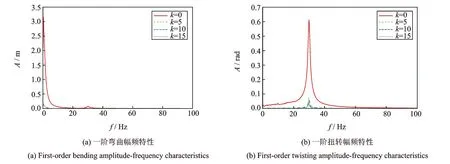
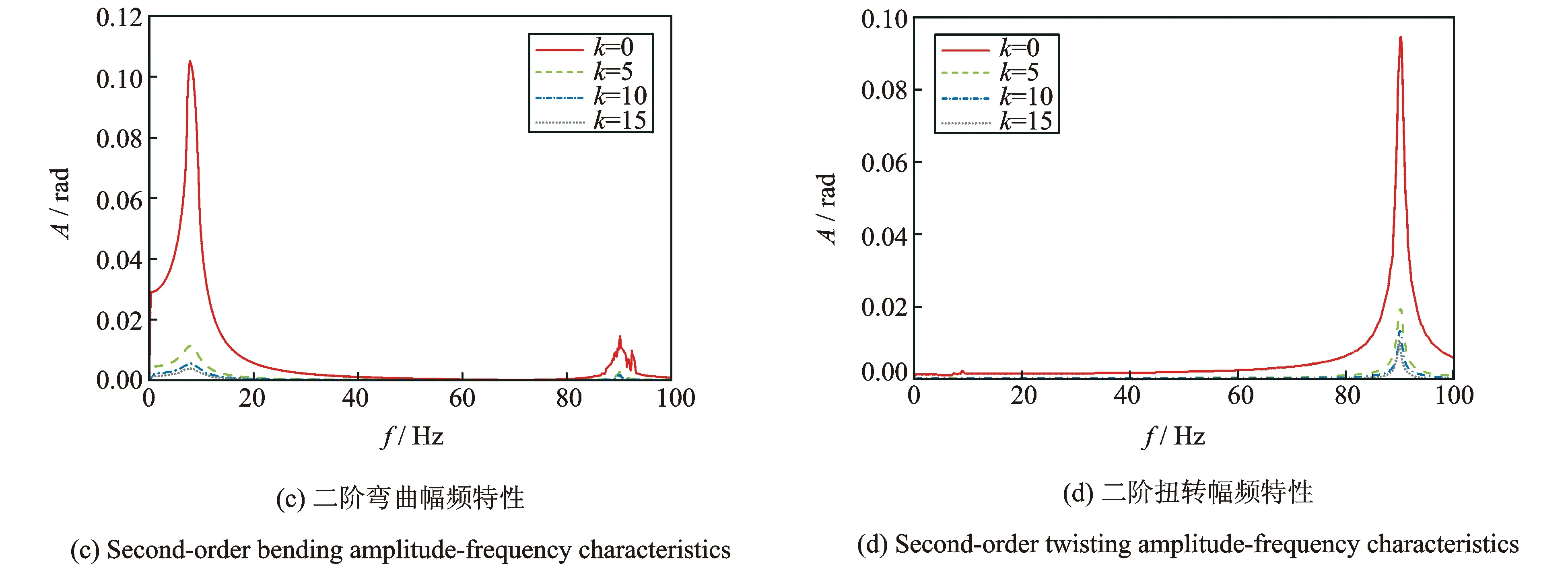
图2 合成射流抑制颤振的效果

3 结 论

本文建立复合材料三元机翼动力学模型，并研究了合成射流初始相位与涡脱相位间的关系。据此，本文提出了合成射流抑制机翼失速颤振的相位控制方法。以NACA0012翼型为例，数值验证了该方法的效果，并得出如下结论：

(1)合成射流频率靠近涡脱基频时，合成射流可控制涡脱的相位。

(2)合成射流的相位控制方法可减小脉动气动载荷在各阶振型上的投影幅值，从而实现抑制机翼失速颤振。

致谢

感谢国防科学技术大学航天与材料工程学院的罗振兵副教授在本文研究中给予的有益帮助。

参考文献:

[1] 吴志刚,杨超.主动气动弹性机翼的颤振主动抑制与阵风减缓研究[J].机械强度,2003, 25(1):32—35.Wu Zhigang, Yang Chao. Investigation on active flutter suppression and gust alleviation for an active aeroelastic wing[J]. Journal of Mechanical Strength, 2003,25(1):32—35.

[2] 罗振兵,夏智勋.合成射流技术及其在流动控制中应用的进展[J].力学进展，2005,35(2):221—234.Luo Zhenbing, Xia Zhixun. Advances in synthetic jet technology and applications in flow control[J]. Advances in Mechanics, 2005,35(2):221—234.

[3] Ryan H, Quentin G, Bruce C. Interaction of adjacent synthetic jets in an airfoil separation control application[J]. AIAA Paper, 2003:3 709(2003).

[4] Catalin N. Synthetic jets influence on NACA 0012 airfoil at high angles of attack[J]. AIAA Paper, 1998:4523(1998).

[5] Smith B L, Glezer A. Vectoring and small scale motions affected in free shear flows using synthetic jet actuators[J]. AIAA Paper, 1997:0213(1997).

[6] Breuker R De, Abdalla M, Marzocca P. Aeroelastic control and load alleviation using optimally distributed synthetic jet actuators[A]. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference[C]. Honolulu, USA, 2007.

[7] Milanese A, De Breuker R, Marzocca P, et al. Distributed synthetic jet actuators for the control of nonlinear aeroelastic systems[A]. 19th International Conference on Adaptive Structures and Technologies[C]. Ascona, Switzerland, 2008.

[8] Palaniappan K, Sahu P, Jameson A, et al. Design of adjoint based laws for wing flutter control[A]. 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition[C]. Orlando, USA, 2009.

[9] Armanios E A, Badir A M. Free vibration analysis of anisotropic thin-walled closed-section beams[J]. AIAA Journal, 1995,33(10):1 905—1 910.

[10] 金琰,袁新,申炳録.机翼大攻角下失速颤振的气动弹性研究[J].工程热物理学报,2002,23(5):573—575.Jin Yan, Yuan Xin, Shen Byeong-Rog. Aeroelastic analysis of an airfoil′s stall flutter at large mean incidence angle[J]. Journal of Engineering Thermophysics, 2002,23(5):573—575.

[11] 王晋军,冯立好,徐超军.合成射流控制圆柱分离及绕流结构的实验研究[J].中国科学,2007,37(7):944—952.Wang Jinjun, Feng Lihao, Xu Chaojun. Experimental study on synthetic jet controlling the cylindrical separation and the streaming structure[J]. Science in China Press, 2007,37(7):944—952.