座椅悬架不匹配干扰估计全程滑模控制研究
朱 跃, 朱思洪, 肖茂华
(南京农业大学工学院, 江苏 南京 210031)
引 言
座椅悬架是车辆系统的重要组成部分,近年来通过座椅悬架的主动/半主动控制来降低车辆振动,提高驾驶平顺性和乘坐舒适性,业已成为研究的热点[1~7]。然而,由于座椅悬架是一类多自由度的复杂振动系统,并且地面激励常常以持续干扰的形式作用于系统中,而且随着座椅悬架的使用,系统中的相关阻尼系数、刚度系数不可避免发生一些变化;此外驾驶人员及负载的变化也是必然存在。所以,实现座椅悬架系统的良好控制非常具有挑战性。目前,部分学者正在尝试着把一些先进控制方法用于座椅悬架控制系统中。文[1]针对带有电流变阻尼器的座椅悬架系统设计了滑模控制器,但是没有分析阻尼系数和刚度系数变化对系统的影响。文[2]针对座椅悬架系统设计了H-inf控制器,没有区分匹配干扰和不匹配干扰,而且需要全部的状态变量进行反馈控制。文[3]针对带有磁流变减振器的二自由度座椅悬架系统,设计了基于积分滑模的控制器,没有考虑人体动态的影响。文[4]基于传统滑模控制思想,设计了车辆半主动悬架控制系统,仅仅考虑了匹配干扰的影响。因此,本文的研究目的是针对含有人体动态的三自由度座椅悬架系统,同时考虑系统中存在的匹配干扰和不匹配干扰的影响,仅仅基于输出变量而不是全部状态变量,为座椅悬架系统构造全程滑模输出反馈控制器。
本文通过选择合适的状态变量及干扰变量,将地面激励视为可从控制通道输入的匹配干扰。对于系统中不可避免会发生的质量、阻尼系数和刚度系数变化,本文将这类干扰视为不从控制通道输入的非匹配干扰,并为之设计了非匹配干扰估计器。基于Lyapunov理论,设计滑模控制器,并证明了系统的鲁棒稳定性。基于座椅位移和人体加速度,利用滑模观测器,实现了对系统状态变量的观测。
1 座椅悬架模型
考虑三自由度的座椅悬架系统[7],如图1所示。其中,m1,m2,m3分别为座椅、大腿臀部及坐垫、人体上身的质量;z1,z2,z3分别为相应的位移;k1,k2,k3和c1,c2,c3为相应的刚度系数和阻尼系数(其中k3,c3用来表征人体内部如脊柱等部分引起的刚度系数和阻尼系数)。u是可用于控制设计的减振器可变阻尼力,z0为外界路面对系统的位移激励。本文中假设悬架系统仅存在垂直运动,忽略俯仰及旋转运动。
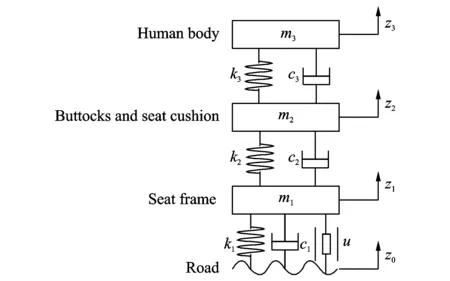
图1 三自由度座椅悬架系统
根据图1可知系统的动态模型为
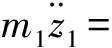
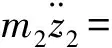
(1)
y=Cx
(2)
其中
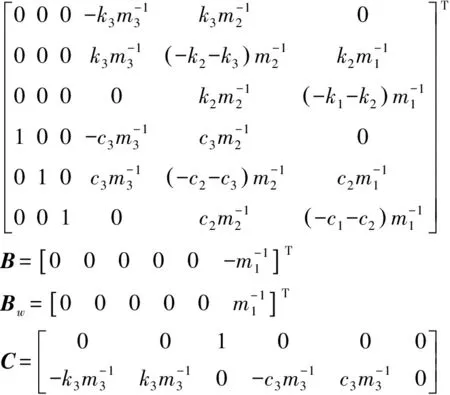
考虑到mi,ki,ci(i=1,2,3)不可避免存在一些摄动,假设
(3)
状态方程(1)从而扩展为
(4)
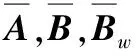
(5)
其中,fu=ΔAx表示不匹配干扰项,Bfm=ΔBu+(Bw+ΔBw)w表示匹配干扰项。
对于fu和fm,做如下假设
(6)
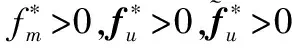
此外,假设(A,B)可控,(A,C)可观。
2 座椅悬架滑模控制
由座椅悬架状态方程式(5)可知,系统动态方程的干扰由匹配干扰Bfm和不匹配干扰fu两部分组成,鉴于滑模控制方法对匹配干扰具有绝对鲁棒性这一良好特点[8],并且来自地面的干扰量w为一类持续的干扰这一特性,本文通过设计全程滑模面来处理匹配干扰Bfm,而对不匹配干扰fu则采用不匹配干扰估计器来抑制。
2.1 全程滑模切换函数设计
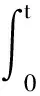
KpE1(t)X1(0))
(7)
其中,E2(t)=diag[e-λ21t,e-λ22t,e-λ23t],E1(t)=diag[e-λ11t,e-λ12t,e-λ13t],Re(λij)>0(i=1,2;j=1,2,3)为滑模态移动参数,X1(0)和X2(0)分别表示X1和X2的初始值。
不难发现,当t=0时,有S=0成立,因此,系统的状态从一开始就位于切换面上,式(7)是一类全程滑模切换函数。当合理设计控制力,使得状态保持在切换函数面上时,系统将不存在经典滑模控制系统中的滑模到达过程。
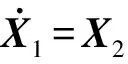
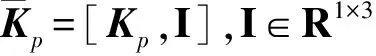
(8)
2.2 不匹配干扰估计器(NMDO)设计
针对不匹配干扰项fu,设计如下不匹配干扰估计器
(9)
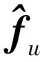
由于在全程滑模控制的作用下,滑模切换面上对匹配干扰Bfm具有完全鲁棒性,因此有
(10)
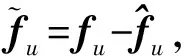
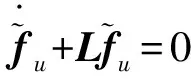
2.3 滑模控制器设计
定理1:在滑模控制律(11),全程滑模切换函数(7)和不匹配干扰估计器(9)的作用下,当条件(6)和(12)成立时,座椅悬架系统是鲁棒稳定的。
(11)
(12)
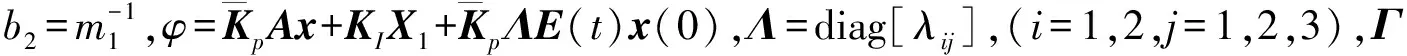
证明:由悬架系统状态方程(5)和滑模切换函数(8)可得
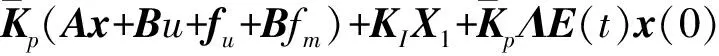
(13)
将滑模控制律(11)带入(13),有
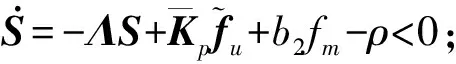
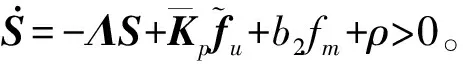
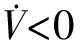
2.4 滑模观测器设计
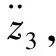
(14)
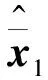
线性变换矩阵T可有多种选择,其中一种合适的是T=T2×T1,
2.5 基于NMDO的座椅悬架全程滑模控制系统结构图
基于NMDO的座椅悬架全程滑模控制系统结构图如图2所示。
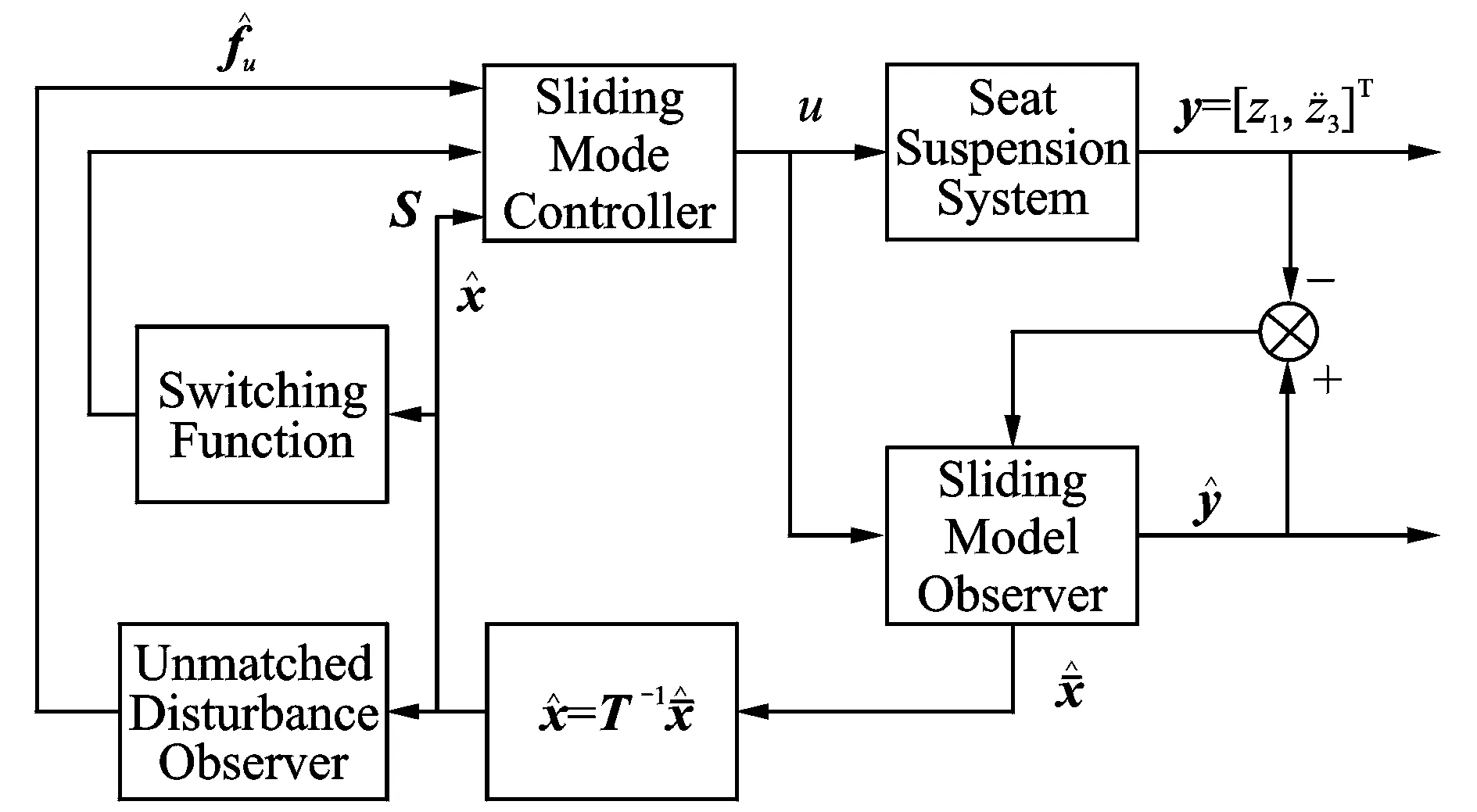
图2 基于NMDO的悬架全程滑模控制系统结构图
3 仿真验证
本文仿真座椅悬架系统的参数来自于文[1,2,13],m1=15 kg,m2=1(坐垫)+7.8(臀部) kg,m3=43.4 kg,k1=31 000 N/m,k2=18 000 N/m,k3=44 130 N/m,c1=830 N s/m,c2=200 N·s/m,c3=1 485 N·s/m。
文中针对以下四种情况进行仿真:
第一种(Case 1):假设地面激励为某种冲击形式,地面激励位移z0如下式及图3所示
(15)
式中 地面质量块高度为a=0.1 m,长度为l=2 m,假设前行速度v0=30 km/h。
第二种(Case 2):假设在冲击形式的地面激励情况下,系统中mi,ki,ci(i= 1,2,3)发生某些变化,如下式所示
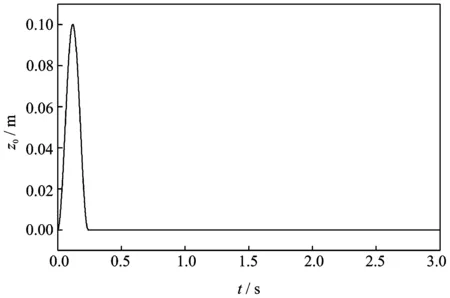
图3 地面激励位移(Case 1 和 Case 2中)
m1=15×150%,m2=1+7.8×150%,m3=43.4×150%,
k1=31 000×70%,k2=18 000×70%,k3=44 130×70%,
c1=830×70%,c2=200×70%,c3=1 485×70%
(16)
第三种(Case 3):假设行驶的地面为D级地面,地面不平度功率谱密度满足Gq(n0)=256×10-6,n0=0.1,前行速度v0=30 km/h。地面激励位移量图4所示。
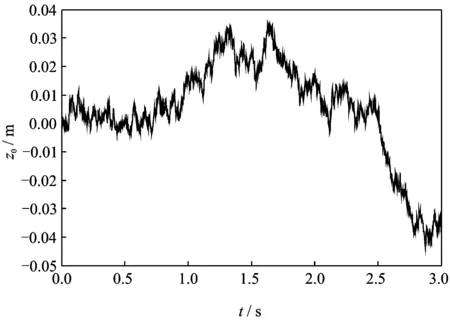
图4 地面激励位移(Case 3 和 Case 4中)
第四种(Case 4):假设地面激励如图4所示,同时系统中mi,ki,ci(i= 1,2,3)发生如式(16)所示的变化。
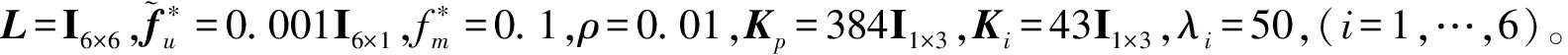
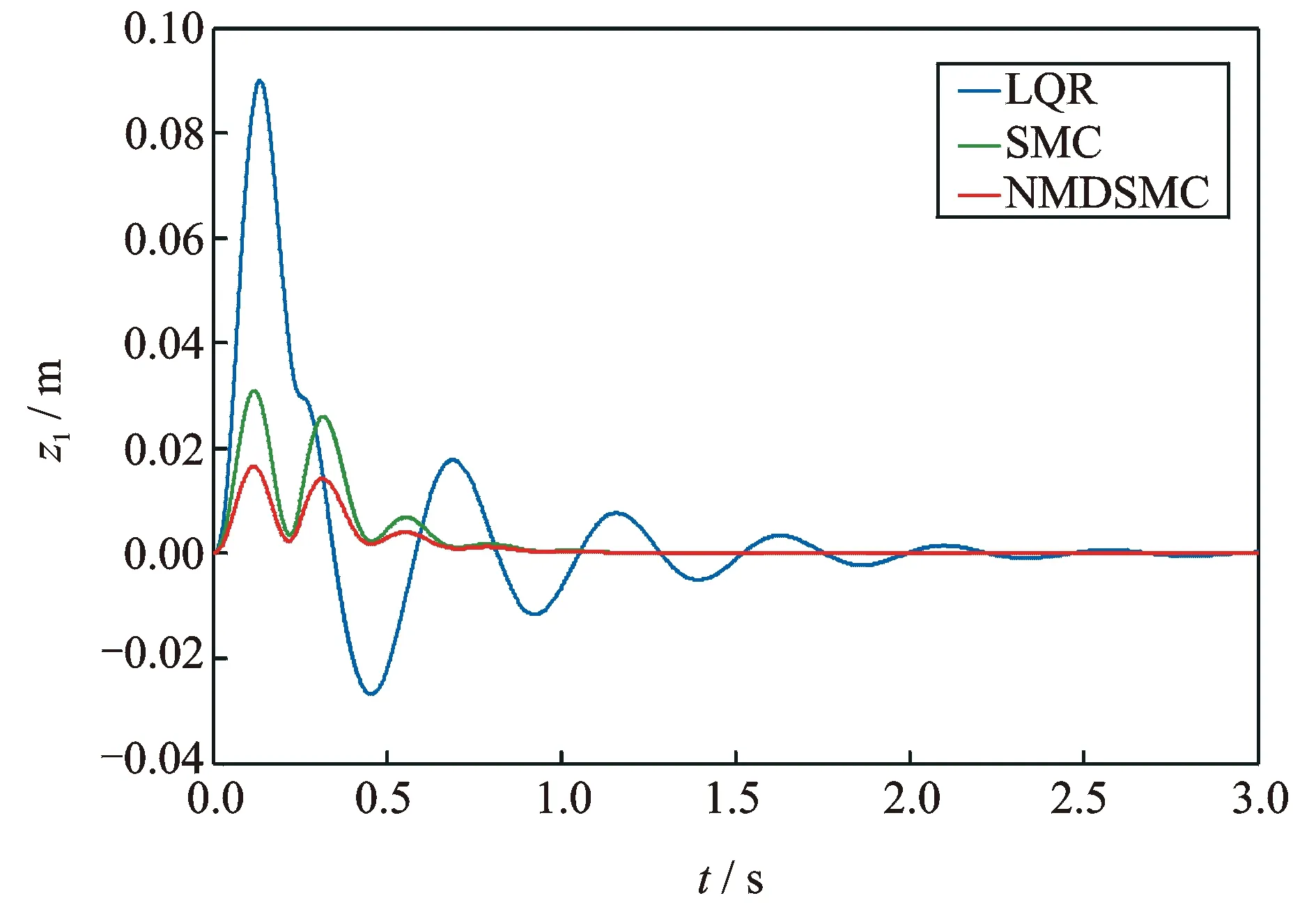
图5 座椅位移(Case 1)
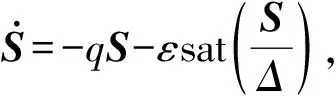
LQR控制器中选择设计参数Q=103I6×6,R=1。
此外,表1,2对三种控制器作用下的座椅位移及人体加速度的RMS值进行了对比,
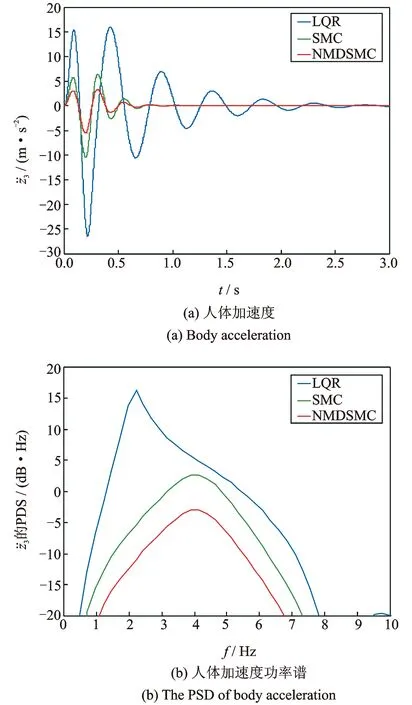
图6 人体加速度及其功率谱(Case 1)
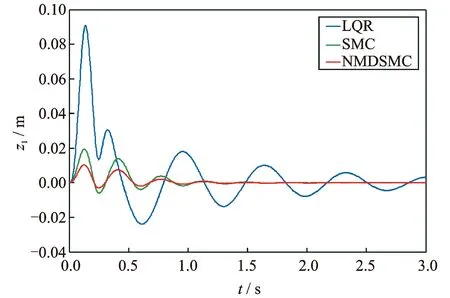
图7 座椅位移(Case 2)
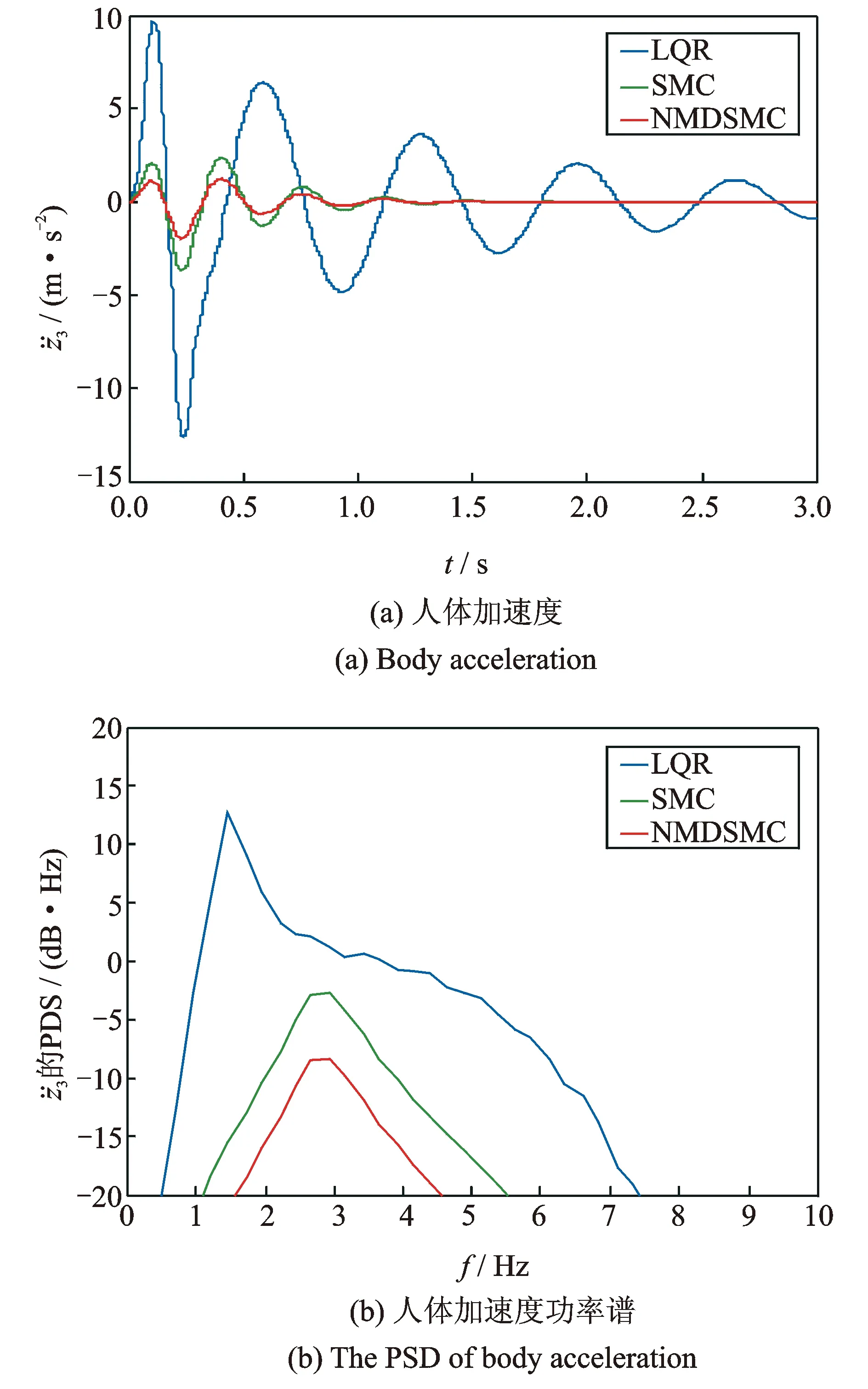
图8 人体加速度及其功率谱(Case 2)
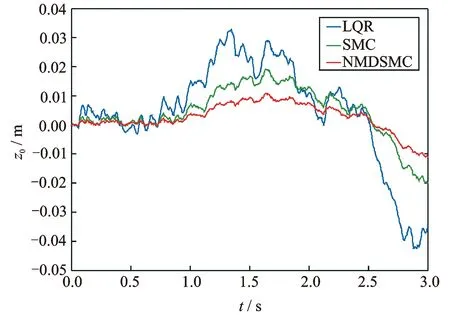
图9 座椅位移(Case 3)
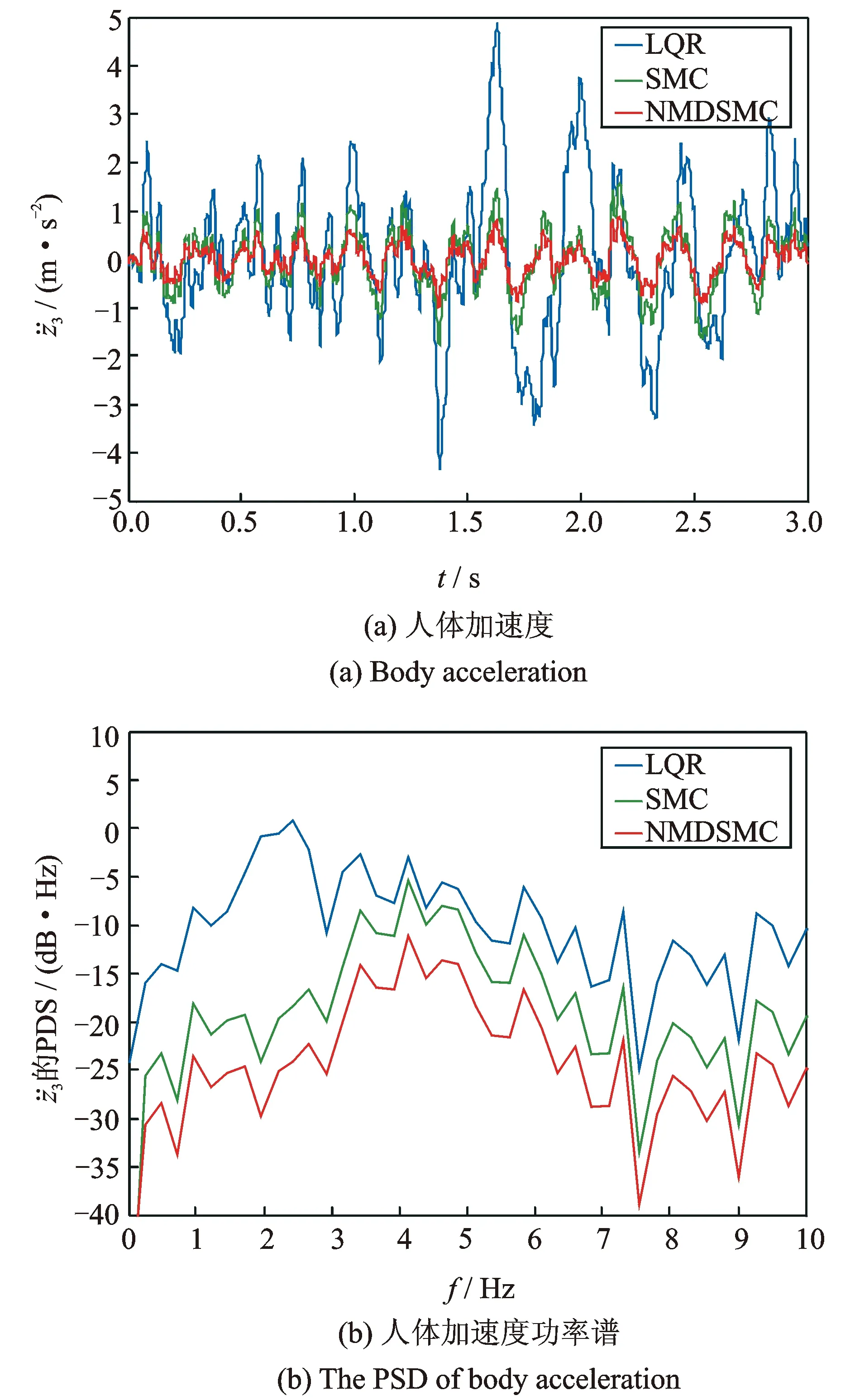
图10 人体加速度及其功率谱(Case 3)
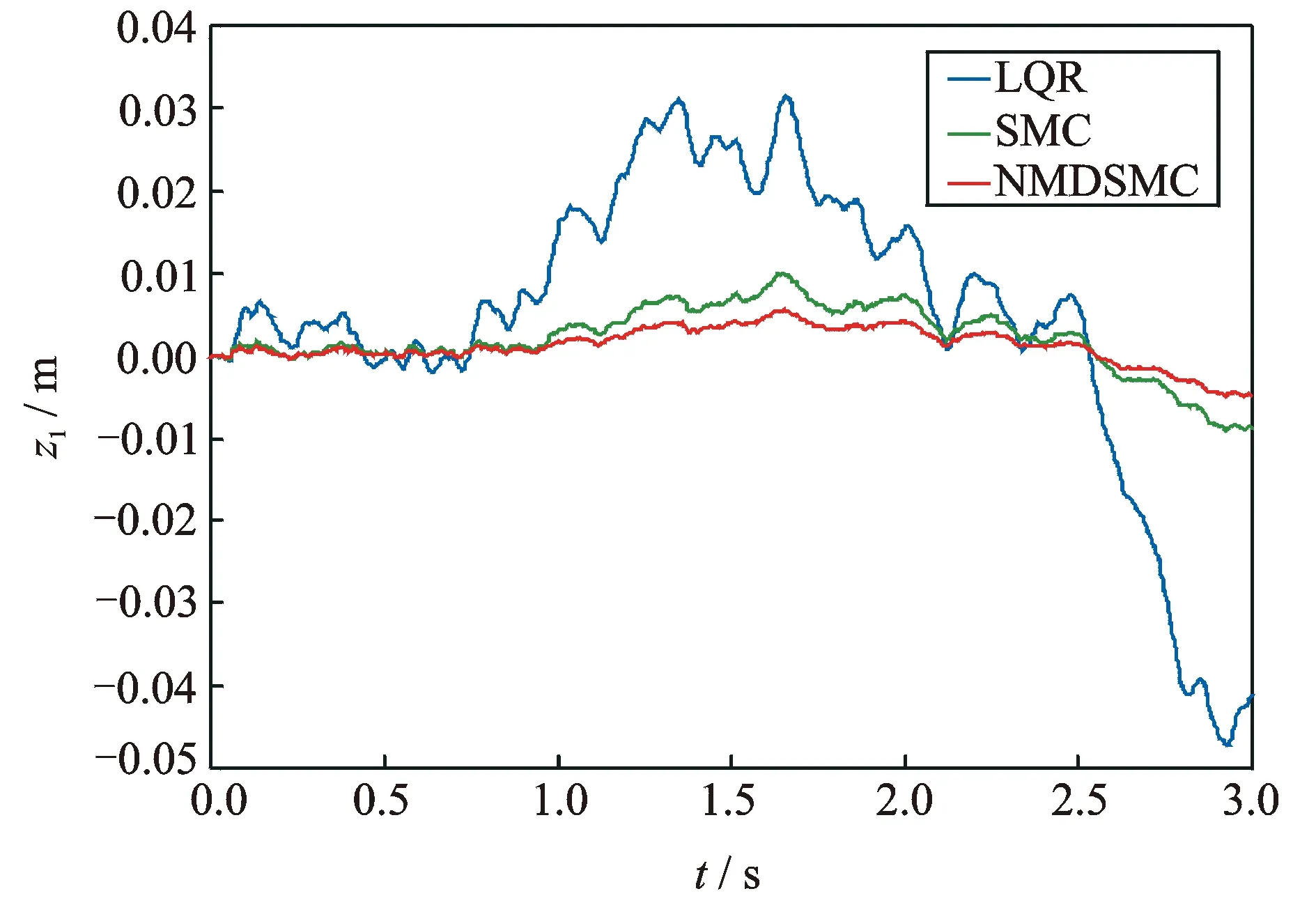
图11 座椅位移(Case 4)
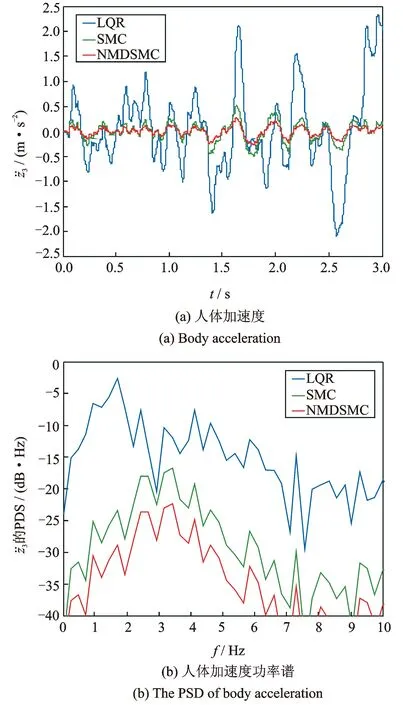
图12 人体加速度及其功率谱(Case 4)
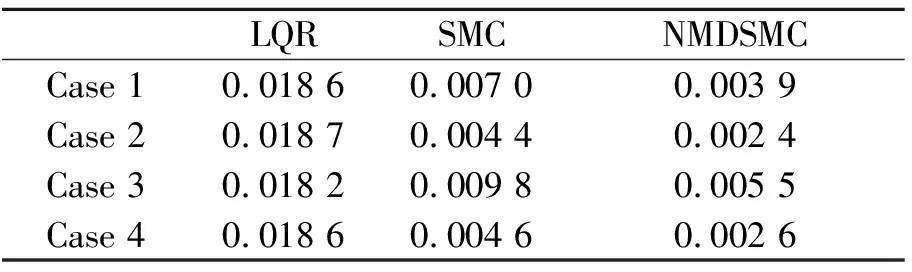
表1 三种控制器作用下的座椅位移RMS值对比
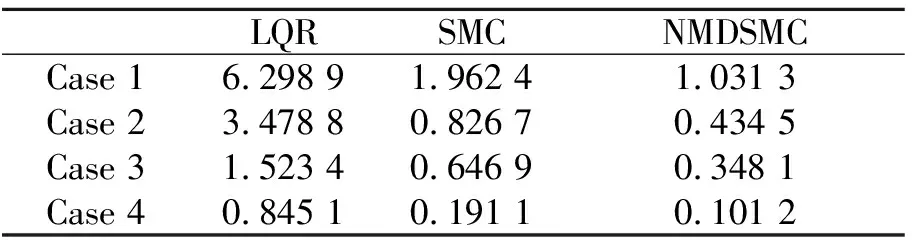
表2 三种控制器作用下的人体加速度RMS值对比
从图5~8中可以发现,针对地面冲击形式的激励,本文所提方法可以有效降低座椅位移及人体加速度幅值,具有更快的收敛速度;在4~8 Hz这个人体敏感的频率区域内,就所比较的三种方法中,人体加速度的振动分贝数在本文方法下最低;当系统中质量、刚度系数、阻尼系数发生变化时,本文方法相比于其他两种方法,具有更强的鲁棒性。
图9~12表明,针对D级地面这种恶劣地况,相对于滑模控制器(SMC)和LQR控制器,本文所设计的控制器(NMDSMC)可以使得座椅位移及人体加速度的幅值变化最为平滑,人体加速度的振动分贝数最低,对系统中的质量、刚度系数、阻尼系数变化鲁棒性最强。
从表1,2不难发现,座椅位移和人体加速度RMS值,在四种情况下,本文方法均具有最小值。
4 结 论
1)针对含人体动态的座椅悬架系统,基于滑模控制理论,实现了座椅悬架系统的良好控制。
2)由于滑模控制仅仅对于匹配的干扰具有完全鲁棒性,而当座椅悬架系统中的质量、刚度系数、阻尼系数发生变化时,对于系统而言,相当于受到了一类不匹配干扰的影响,因此,本文设计了不匹配干扰估计器,用于处理这一问题。
3)考虑到座椅悬架系统仅仅座椅位移量和人体加速度量是可测量的输出量,本文通过合适的可逆线性变换矩阵,采用滑模观测器,实现了对状态变量的观测。
参考文献:
[1] Choi Seung-Bok, Han Young-Min. Vibration control of electro rheological seat suspension with human-body model using sliding mode control[J]. Journal of Sound and Vibration, 2007,303:391—404.
[2] Zhao Yingbo, Sun Weichao, Gao Huijun. Robust control synthesis for seat suspension systems with actuator saturation and time-varying input delay[J]. Journal of Sound and Vibration, 2010,329:4 335—4 353.
[3] 朱茂飞,陈无畏,祝辉.基于磁流变减振器的半主动悬架时滞变结构控制[J].机械工程学报,2010,46(12):113—120.ZHU Maofei, CHEN Wuwei, ZHU Hui. Time-delay variable structure control for semi-active suspension based on magneto-rheological damper[J]. Journal of Mechanical Engineering, 2010,46(12):113—120.
[4] 陈云微,赵强.车辆半主动座椅悬架滑模变结构控制[J].哈尔滨工程大学学报,2012,33(6):775—781.Chen Yunwei, Zhao Qiang. Sliding mode variable structure control for semi-active seat suspension in vehicles[J]. Journal of Harbin Engineering University, 2012,33(6):775—781.
[5] Gao Huijun, Zhao Yingbo, Sun Weichao. Input-delayed control of uncertain seat suspension systems with human-body model[J]. IEEE Transactions on Control Systems Technology, 2010,18(3):591—601.
[6] Sun Weichao, Zhao Ye, Li Jinfu, et al. Active suspension control with frequency band constraints and actuator input delay[J]. IEEE Transactions on Industrial Electronics, 2012,59(1):530—538.
[7] Wei L, Griffin J. The prediction of seat transmissibility from measures of seat impedance[J]. Journal of Sound and Vibration, 1998,214(1):121—137.
[8] 高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1998.
[9] Chen W H. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles[J]. Journal of Guidance Control and Dynamic, 2003,26(1):161—166.
[10] Jun Yang, Shihua Li, Xinghuo Yu. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2013,60(1):160—169.
[11] Utkin V I, Guldner J, Shi J. Sliding Mode Control in Electromechanical Systems[M]. Taylor & Francis, USA, 1999.
[12] Kim K H, Kim P J, You K H. Ultra-precision positioning system using robust sliding mode observer and control[J]. Precision Engineering, 2013,37:235—240.
[13] Liang Cho-Chung, Chiang Chi-Feng. A study on biodynamic models of seated human subjects exposed to vertical vibration[J]. International Journal of Industrial Ergonomics, 2006,36:869—890.

