非自由声场三维重现的扬声器系统优化配置

廖祥凝， 郑四发， 彭 博， 连小珉

(清华大学汽车安全与节能国家重点实验室， 北京 100084)

引 言

声场重现作为研究声品质主观评价及噪声主动控制的一种重要手段，重现系统包括扬声器、麦克风、控制单元等，其中扬声器和麦克风的配置会影响声场重现的精度和准确度[1～3]。因此，如何优化扬声器系统，减少扬声器的个数以简化系统，同时减少扬声器激励信号的计算量具有重要意义。

目前针对不同类型的优化问题发展出诸多优化算法，比如运用于线性系统的梯度下降法、拉格朗日乘数法等；运用于非线性系统及复杂问题的模拟退火算法、遗传算法等。文献[1]利用遗传算法优化扬声器和麦克风的位置，重建与目标声场基本相同的反声场可达到减少机舱内噪音声压50%的效果；文献[2，3]采用施密特正交原理进行了扬声器配置优化的仿真。但在扬声器个数较多的情况下，施密特正交算法存在不稳定性，随着迭代次数的增加，误差累积导致向量不再正交。尤其是重建非自由场环境下的目标声压时，扬声器激励信号的计算量增加，影响到扬声器系统优化的稳定性。针对此问题，本文提出了综合采用传递函数法和QR算法的扬声器优化配置方法。

1 非自由场三维声场重现的控制方法

1.1 三维声场重现的边界控制方法

声场重现技术是基于物理特征参量模拟的三维虚拟空间听觉再现方法，人为地在听者身处的物理空间内构造出虚拟现实的声音，尽可能还原目标声场的听感信息[4]。由空间声场边界控制原理(Boundary surface control principle, BOSC)可知[5]，在封闭空间没有其他声源的情况下，封闭空间的内部声压特性完全取决于边界声压特性。因此，若要重现某区域内的声场，则可通过控制边界声压与目标声压匹配来实现。图1左所示边界∂V包围内部空间V，形成封闭空间，n为边界外法向量，则内部任意点声压表达式为[6]

(1)

式中ρ0为介质密度；f为频率；ω为圆频率；s表示内部点的位置向量；r表示边界点的位置向量；p(s,f)和p(r,f)分别为内部点声压和边界声压；vn(r,f)为边界外法向速度；G(r|s,f)为自由空间的格林函数[6]。

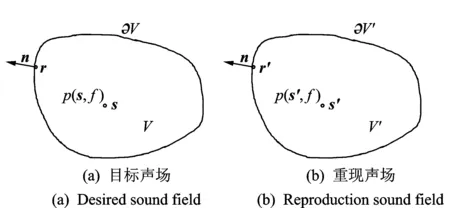
图1 目标声场及重现声场边界控制示意图

类似地，图1(b)为在实验室特定重现区域内声场表示为

(2)

式中r′为∂V′重建声场区域边界上的点；s′为重建区域内部点。

在保证重现区域与目标区域一致的前提下，若想满足重建声场等于目标声场，即边界包围的封闭空间内的声场p(s,f)=pre(s′,f)，通过令式(1)与式(2)相等，可得到

(3)

如果重现执行系统采用无指向麦克风配置，应用狄利克雷(Dirichlet)格林函数[7]，公式(1)，(2)可改写为：

(4)

(5)

式中GD(r|s,f)，GD(r′|s′,f)均为Dirichlet格林函数。

结合边界控制原理和公式(4)，(5)，此时若想满足重现声场与目标声场一致，则只需满足重现区域和目标区域的边界声压相等。即

p(r,f)=pre(r′,f)

(6)

综上所述，若满足重现区域内没有其他声源存在，区域大小与目标区域一致，并且重现执行系统采用无指向麦克风配置的条件，则控制重现区域和目标区域边界声压相等即可使得区域内声压相等，实现重现目的。

1.2 基于声场传递函数求扬声器激励

如图2所示，在带反射的房间内布置L个扬声器和M个麦克风，M个麦克风位置处的重建声压表达式为[8,9]

Pre(f)=H(f)·G(f)

(7)

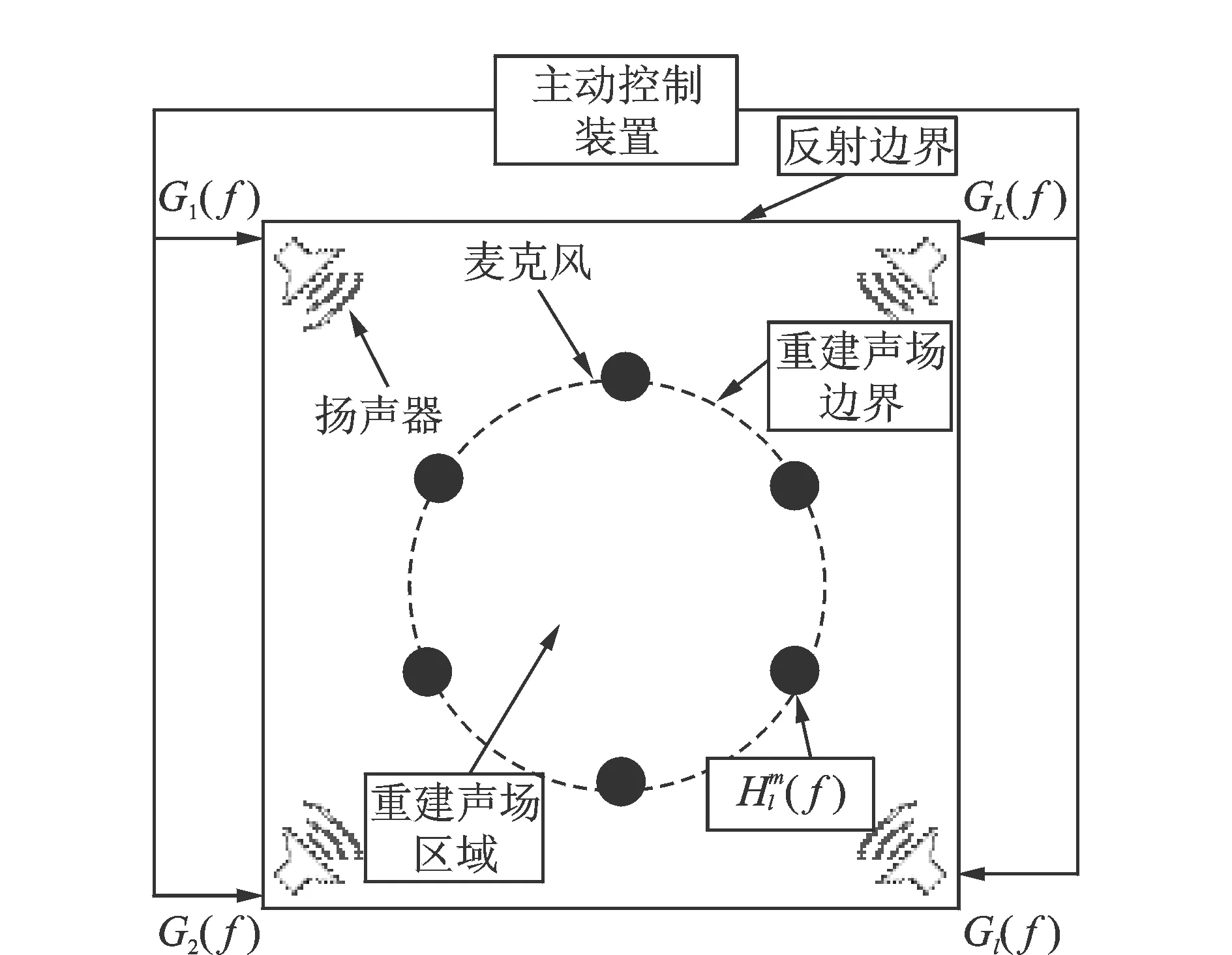
图2 非自由边界的房间声场重现示意图

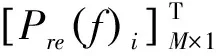
假设M个麦克风处的已知目标声压为Pd(f)，重建目标是使得Pre(f)=Pd(f)，可求得重建目标声场扬声器所需的激励信号

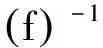
(8)

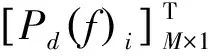
(9)

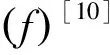
λ(f)GH(f)G(f)

(10)

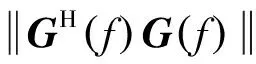
①计算正则化参数λ(f)，选择L-曲线法求解[11]；

②求得λ(f)后，频域范围的激励信号G(f)可由下面步骤解出：

1)当扬声器个数大于麦克风个数，即L>M时，方程(8)为不定方程，则激励信号G(f)解为

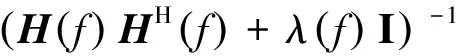
(11)

2)当扬声器个数小于麦克风个数，即L≤M时，方程(8)为超定方程或正定方程，则激励信号G(f)解为

G(f)=(HH(f)H(f)+λ(f)I)-1HH(f)Pd(f)

(12)

式中I为单位矩阵。

2 扬声器系统配置的优化

由于传递函数包含了扬声器和麦克风位置及个数的物理特征，因此扬声器的配置影响着重现声场的准确性。对扬声器系统配置进行优化，有利于满足准确性的同时简化重现系统，更重要的是减少求取扬声器激励信号的计算量，提高声场重现的时间效率。

2.1 扬声器配置优化的步骤

传递函数H(f)为M×L矩阵，可看成由L个列向量组成

(13)

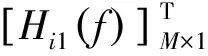
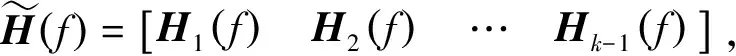
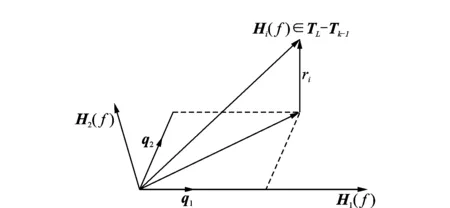
图3 扬声器配置优化示意

引入距离指标Jk-1

Jk-1=max(20lgri(k-1))

(14)

式中ri(k-1)指Hi(f)到Tk-1空间的距离。

若计算式(14)得到的距离指标Jk-1小于某数量值Jthr，如-40 dB(依照重现声场应达到的精度等设定)，则可近似认为剩余的TL-Tk-1空间包括在Tk-1空间内，优化停止，即剩余传递函数对应的扬声器可舍去。

将上述过程描述成如下数学问题：

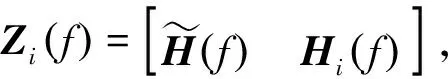
(15)

由式(15)可知，Rmk表示Hi(f)到Tk-1的距离ri(k-1)。可得

Hk(f)=arg(max(ri(k-1)))

(16)

式中 arg表示定义域的子集，即arg(max(g(t)))表示提取出定义域子集中使得函数g(·)最大值的自变量。

对于多频声压信号，如频率范围为[fl,fh]，可以将频率离散为N段，再引入两个距离指标J(k-1)avg和J(k-1)min：

(17)

J(k-1)min=min(Ji(k-1)(fl),…，Ji(k-1)(fh))

(18)

J(k-1)avg用于距离最大条件的判断，J(k-1)min用于优化是否终止的判断。则公式(16)变为

Hk(f)=arg(max(J(k-1)avg))

(19)

2.2 初始扬声器的选择

不同的初始扬声器位置对优化后选择出的扬声器有较大影响，直接影响着重建声场的精准度，因此初始扬声器的正确选择十分重要。从式(1)可知，麦克风采集的声压是由多个扬声器驱动信号的线性叠加，因此选择扬声器传递函数与目标声压向量夹角最小的扬声器作为初始扬声器[2]，如图4所示。即

Hini(f)=arg(min(sinθi))

(20)

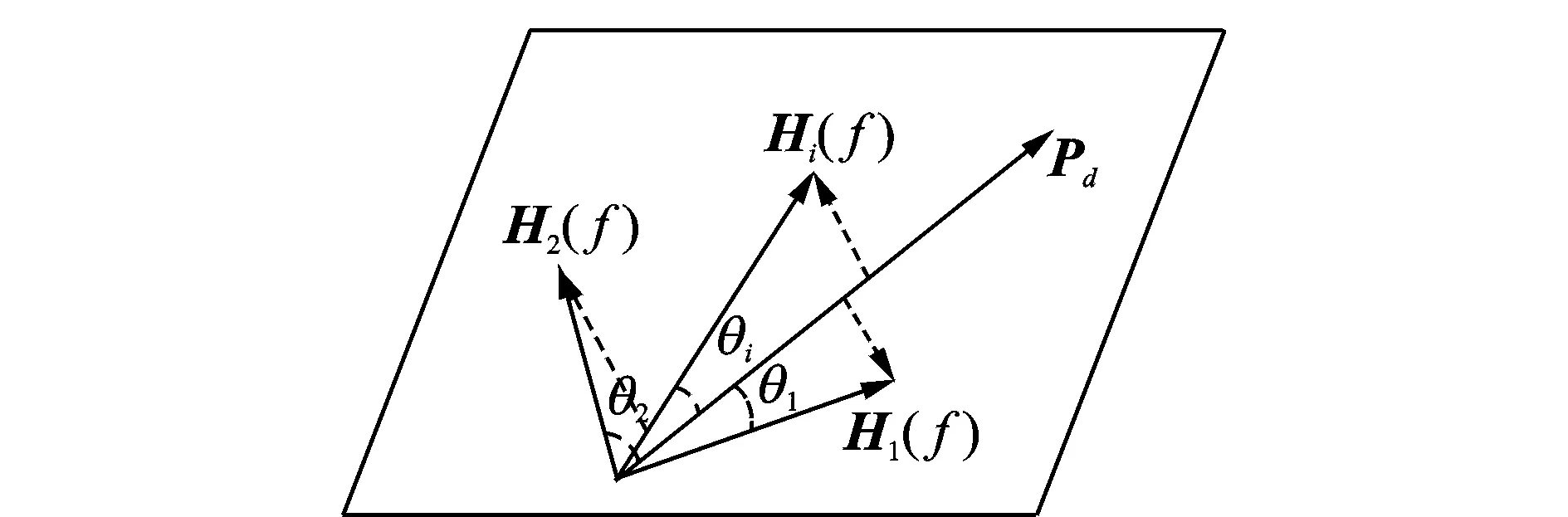
图4 初始扬声器的选择示意图

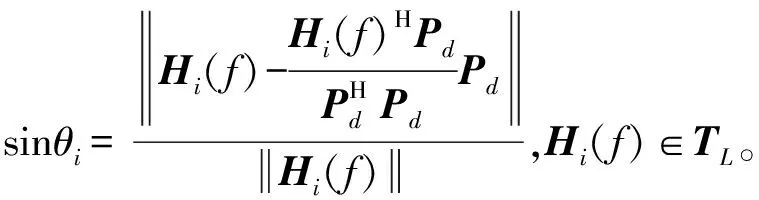
3 扬声器优化方法的验证

3.1 试验环境

三维声场重现在如图5的房间内进行，房间尺寸为4.2 m×3.1 m×2.6 m，初始布置的扬声器(21个)和麦克风(22个)如图5，6所示。其中18个麦克风均匀分布在人工头周围，用于目标声压信号的采集、传递函数的测量以及声场重现；剩余4个麦克风分布在人工头耳朵附近，用于检测重现声场精度。

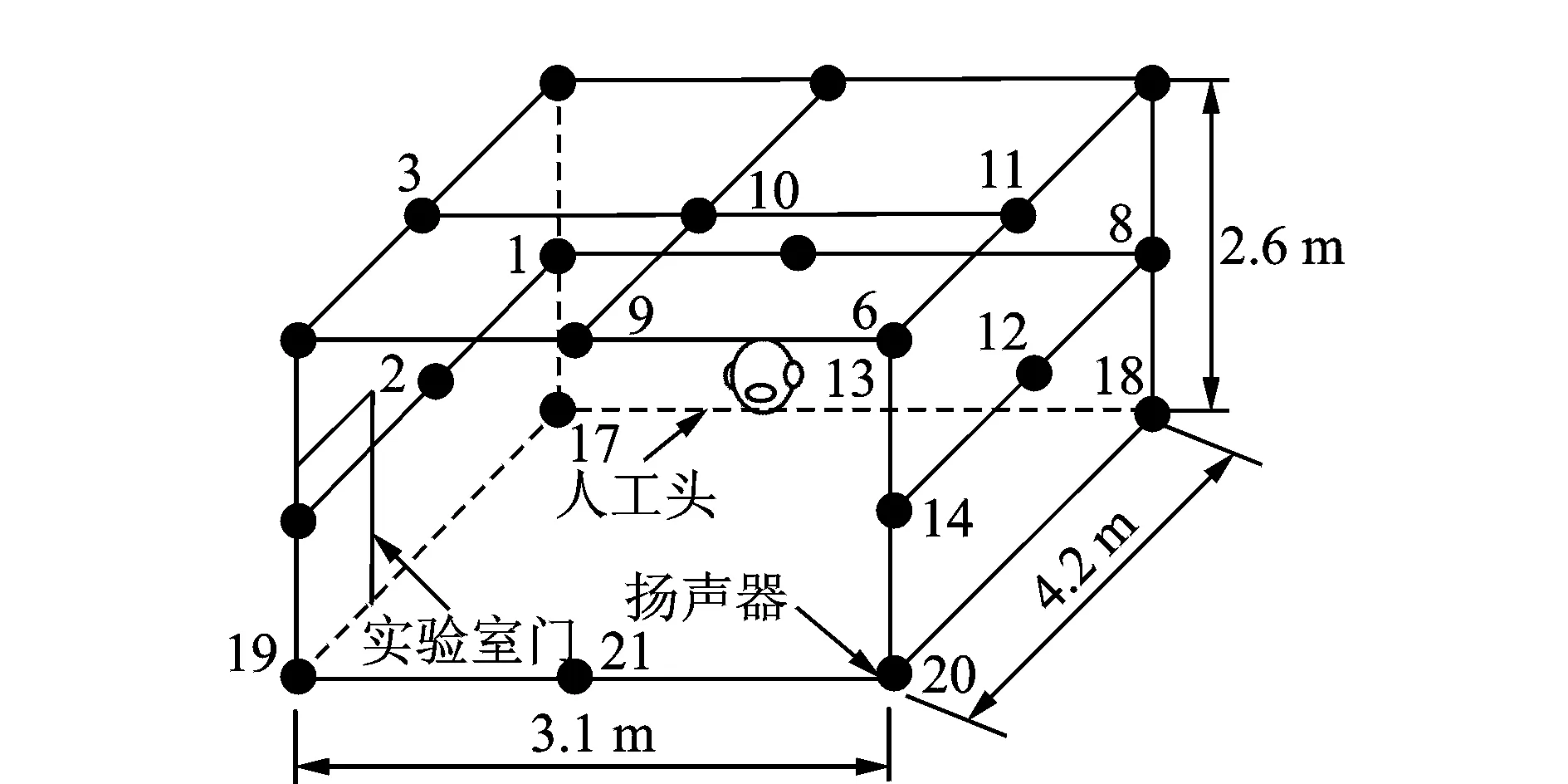
图5 扬声器配置示意图

拟重现的目标声压为汽车匀速行驶过程副驾驶位耳朵附近的噪声，采用同图6相同的传声器阵列进行采集，其中的一个典型的麦克风时域信号如图7所示。

图6 麦克风配置图

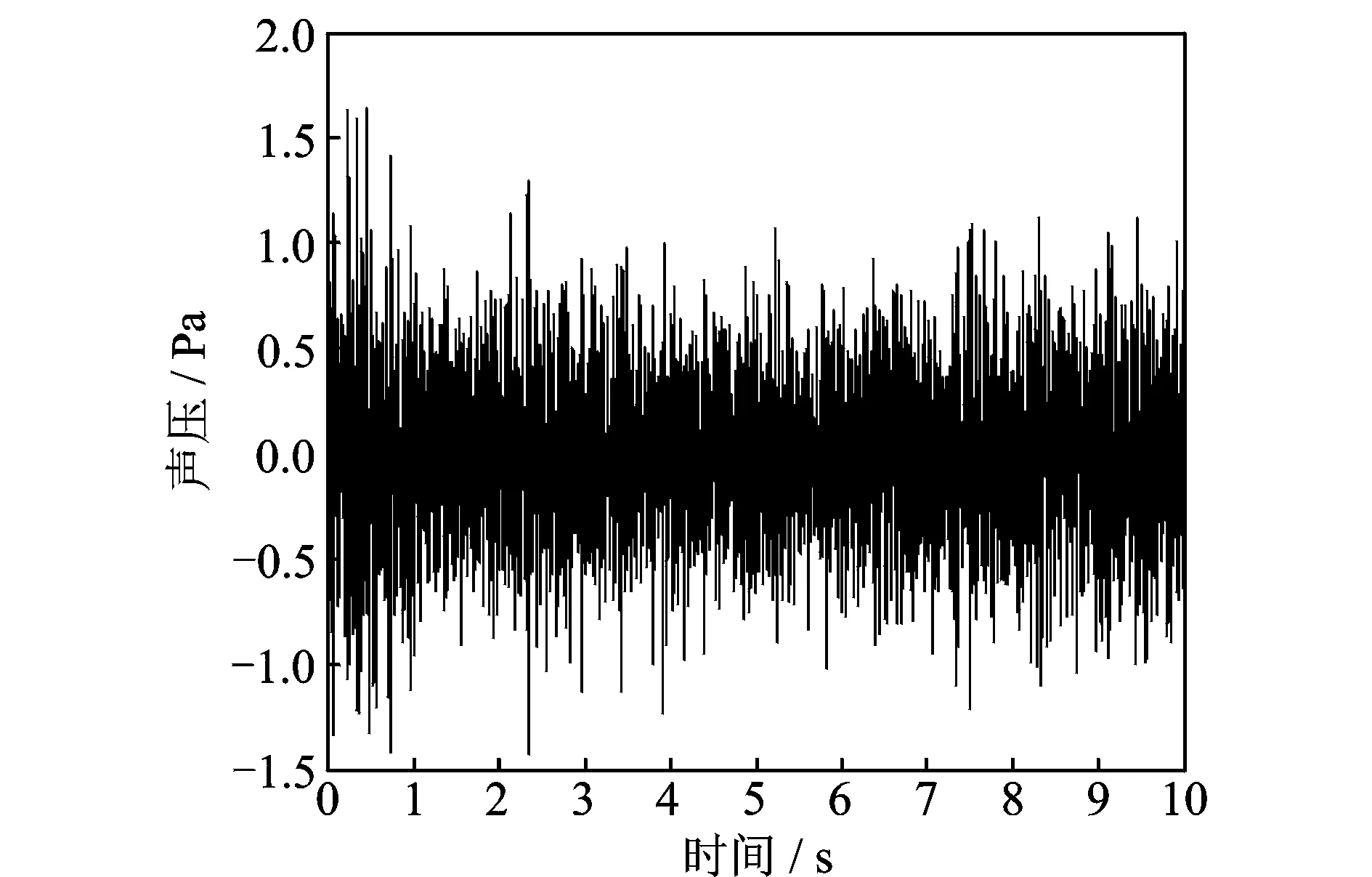
图7 拟重现声场中的声压信号

3.2 实验结果

3.2.1 扬声器优化配置结果

由于扬声器型号不同，只有序列号17到21的扬声器能发出100 Hz以下低频信号，因此分频优化，即序列号前16的扬声器阵列与后5个扬声器阵列分开优化。选取Jthr=-40 dB，运用上述的QR算法得到Jmin和Javg的变化，如图8和9所示。从Jmin可以看出：声场重建控制系统中，优化后的扬声器阵列包括能发出低频信号的5个扬声器以及序列号前16的扬声器阵列经过筛选后留下的6个扬声器，总共11个扬声器，其序列号分别为2，3，5，6，10，16，17，18，19，20，21。相比较于原扬声器阵列数目，优化后的扬声器数目减少了一半。

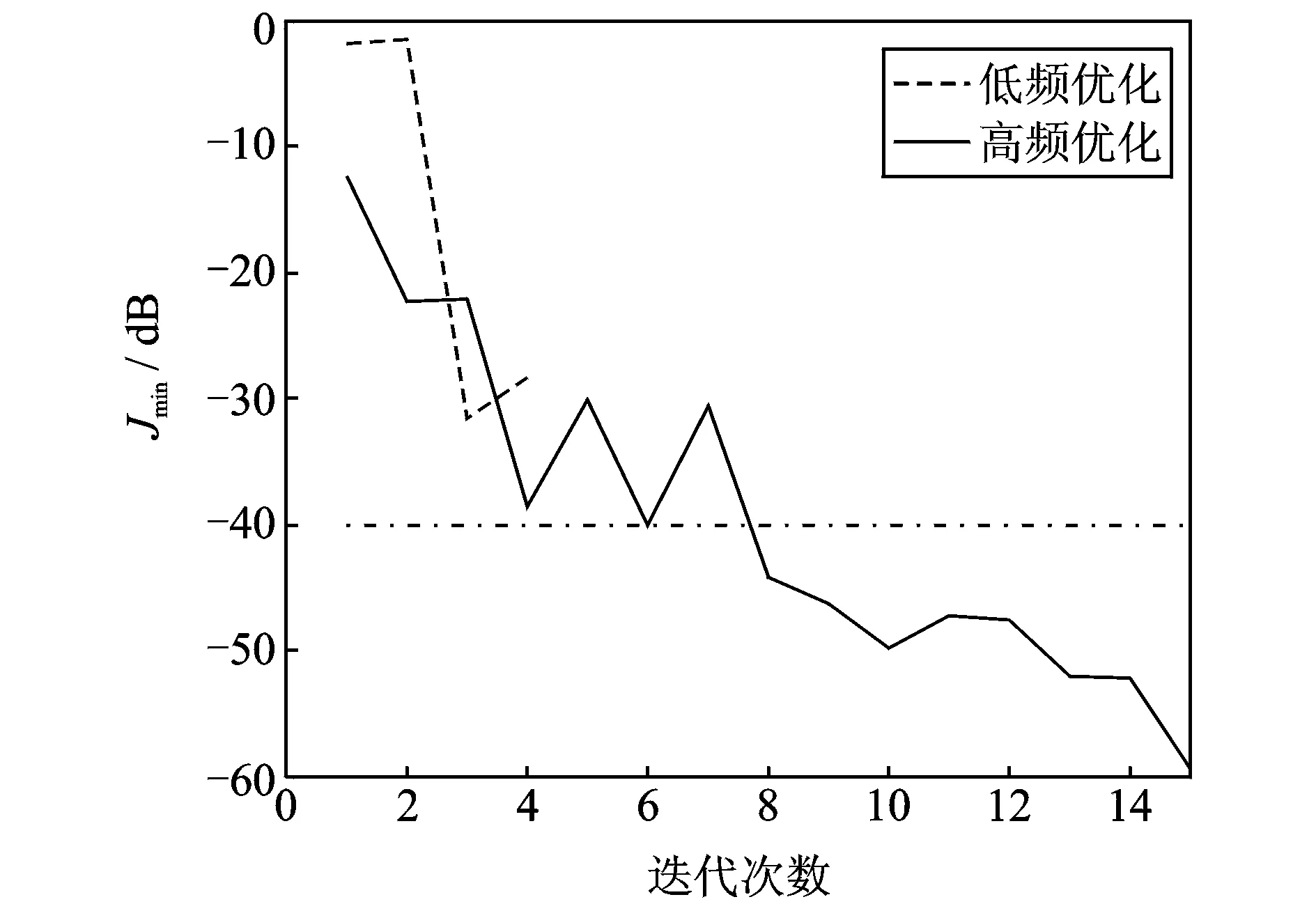
图8 Jmin随迭代次数的变化

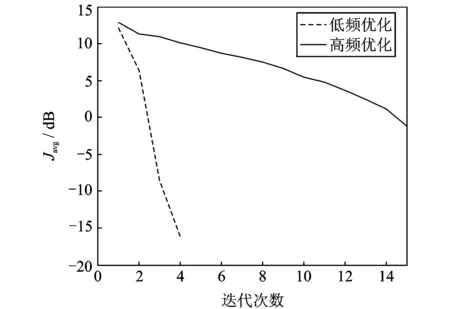
图9 Javg随迭代次数的变化

3.2.2 扬声器配置优化前后重现结果对比

利用优化前21个扬声器与优化后11个扬声器分别进行声场重现，得到如图10所示耳朵附近四检测点时域声压级的结果，其中无优化重现声压信号的平均时域声压级误差为0.47 dB，带优化的平均时域声压级误差为0.51 dB。图11为某一检测点处原声场与无优化、带优化重现声压信号频谱的幅值对比，可看出噪声信号主要包括40～160 Hz范围内的低频成分，目标声压信号与无优化、带优化重现声压信号的幅值曲线都十分吻合。计算得到40～400 Hz范围内，无优化重现声压信号的平均幅值误差为1.84%，带优化的平均幅值误差为2.09%。

综合图10，11对比可以看出，无优化重现声场与优化重现声场都能较好重现目标声场，验证了优化算法的正确性。同时由于优化了扬声器配置，公式(8)中传递函数减少导致计算扬声器重现声场所需激励的时间也相应减少了。无优化时计算扬声器激励信号大约需17 h，而优化后计算扬声器激励信号只需要7.4 h，可见扬声器配置优化算法的应用不仅能保证重现声场的精度，而且大大节省了扬声器激励信号的计算时间。

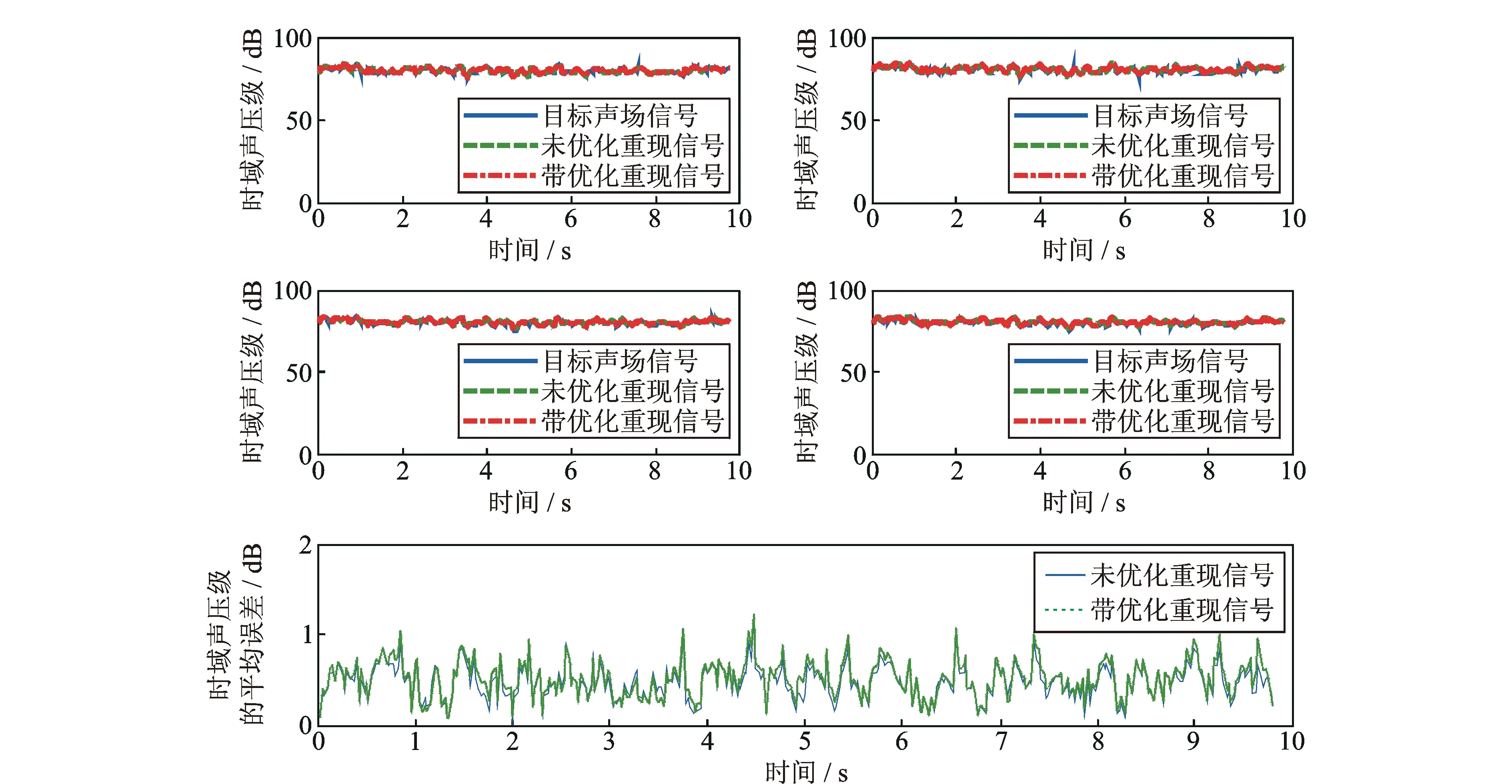
图10 不同扬声器配置下4检测点时域声压级的对比

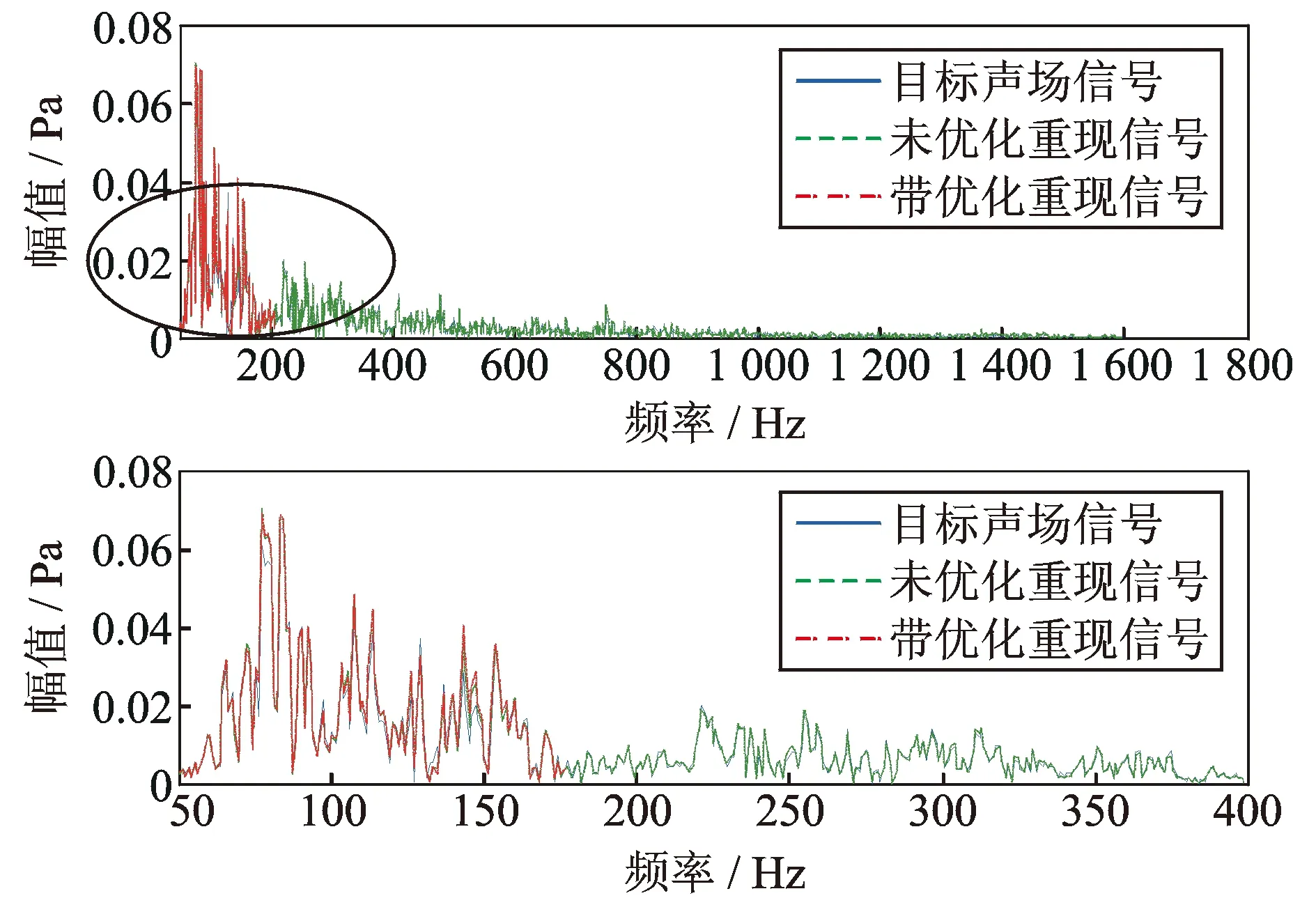
图11 不同扬声器配置下某检测点频域幅值对比

4 结 论

论文以实现三维声场重现为目的，基于声场边界控制方法，综合采用传递函数法和QR算法进行扬声器系统配置优化。其主要思想为选出传递函数中最大线性无关的列向量对应的扬声器，并以实车信号作为目标声场，进行了声场重现试验。通过扬声器系统优化前后的重现声场与目标声场的对比，结果表明：优化后采用更少的扬声器能达到与优化前扬声器配置实现的重现效果，并且优化后减少了求解扬声器信号激励的计算时间，提高了重现效率，证明了扬声器优化方法的有效性。

参考文献：

[1] Diamantis Z G, Tsahalis D T, Borchers I. Optimization of an active noise control system inside an aircraft, based on the simultaneous optimal positioning of microphones and speakers, with the use of a genetic algorithm[J]. Computational Optimization and Applications, 2002, 23(1): 65—76.

[2] Asano F, Suzuki Y, Swanson D C. Optimization of control source configuration in active control systems using Gram-Schmidt orthogonalization[J]. Speech and Audio Processing, IEEE Transactions on, 1999, 7(2): 213—220.

[3] Enomoto S, Ikeda Y, Ise S, et al. Optimization of loudspeaker and microphone configuration for sound reproduction system based on boundary surface control principle[A]. Proc. ICA2010[C]. Sydney, Australia, 2010,2:942—948.

[4] Li Shenguang, Zheng Sifa, Peng Bo, et al. Experimental research on 3D sound reproduction with reflection boundary[A]. Inter-Noise 2012[C]. New York, 2012,5:3 624—3 632.

[5] Epain N, Friot E. Active control of sound inside a sphere via control of the acoustic pressure at the boundary surface[J]. Journal of Sound and Vibration, 2007, 299(3): 587—604.

[6] Fazi F M. Sound field reproduction[D]. Southampton: University of Southampton, 2010.

[7] Ise S. A principle of sound field control based on the Kirchhoff-Helmholtz integral equation and the theory of inverse systems[J]. Acta Acustica United with Acustica, 1999, 85(1): 78—87.

[8] Betlehem T, Abhayapala T D. Theory and design of sound field reproduction in reverberant rooms[J]. The Journal of the Acoustical Society of America, 2005, 117(4): 2 100—2 111.

[9] Peng Bo, Zheng Sifa, et al. 3D sound field reconstruction in reverberation with regularization[A]. Proceedings of 20th International congress on Sound and Vibration, ICSV 2013[C]. Bangkok, Thailand, 2013,1:277—284.

[10] 谢菠荪.头相关传输函数与虚拟听觉[M].北京：国防工业出版社，2008:240—241.Xie Bosun. Head Related Transfer Function and Virtual Auditory[M]. Beijing: National Defense Industry Press, 2008:240—241.

[11] 王振杰, 欧吉坤. 用 L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报(信息科学版), 2004, 29(3): 235—238.Wang Zhenjie, Ou Jikun. Determining the ridge parameter in a ridge estimation using L-curve method[J]. Geometrics and Information Science of Wuhan University, 2004, 29(3): 235—238.