随机参数汽车盘式制动器的稳定性分析

吕 辉， 于德介

(湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082)

引 言

汽车制动噪声已成为城市的主要噪声污染源之一。如果汽车的制动器系统在工作过程中处于不稳定状态，就可能引起强烈的振动，并形成刺耳的噪声。

汽车制动噪声的频率范围很广，尤其以1～16 kHz之间的尖叫声最困扰乘客的听觉，严重影响车辆的舒适性和环保品质[1]。针对汽车制动噪声问题，不少学者通过对制动器系统的复特征值进行分析来判断系统的稳定性，从而预测制动噪声的产生趋势。随着计算技术发展，基于有限元的复特征值分析方法已成为一种研究制动器系统稳定性的有效方法[2,3]。宿等针对影响制动噪声关键子结构的动态特性[4]，按照关键子结构动态特性预定的设计或修改设计方向和目标，在有限元方法的基础上，采用罚函数法与变尺度法相结合优化子结构设计参数，以达到抑制噪声的目的。该研究将系统的各参数作为确定性参数进行研究，没有考虑参数不确定性的影响。Liu等建立了汽车盘式制动器系统的耦合有限元模型[5]，通过求解制动器系统的复模态，分析了各参数对系统稳定性的影响。Liu等在分析各参数对系统稳定性的影响时，先假定系统其他参数不变，再对某一参数进行一系列取值，利用有限元软件求解出主要不稳定模态的阻尼比，从而得出该参数与系统稳定性之间的相互关系。由于该方法需要多次调用有限元模型进行求解，因此计算工作量较大。

工程实际中，材料特性、几何尺寸和作用载荷等参数往往具有不确定性，只有考虑各设计参数的不确定性，才能更好地反映工程实际[6,7]。同时，对工程研究模型进行参数化，可大大减小计算量，避免重复调用工程模型，提高研究效率。响应面法就是其中一种基于试验设计[8]，可快速实现参数化的研究方法，并已广泛运用于汽车材料和工艺等方面。

本文将随机参数引入到汽车盘式制动器的稳定性研究中，采用随机参数对制动器的不确定性进行描述，并将响应面法与有限元复特征值技术相结合，实现了制动器稳定性模型的参数化，进而根据参数化下系统特征值的随机特性对系统稳定性进行分析。对某车的浮钳盘式制动器系统进行研究，分析了随机参数正态分布假设下系统特征值的概率统计特性和参数概率灵敏度，结果表明通过修改制动器系统支撑背板厚度以提高支撑刚度，可有效提高系统的稳定性，从而减小制动噪声产生。

1 汽车盘式制动器稳定性理论

以汽车盘式制动器为研究对象，其简化结构如图1所示，其中制动盘固定在车轮上，随车轮转动；2个制动片分别装在制动盘的两侧，并牢固地粘在支撑背板上。汽车制动过程主要是通过活塞将液压力加载到制动片上，再通过制动片挤压转动中的制动盘，由此产生摩擦阻力而达到减速效果。

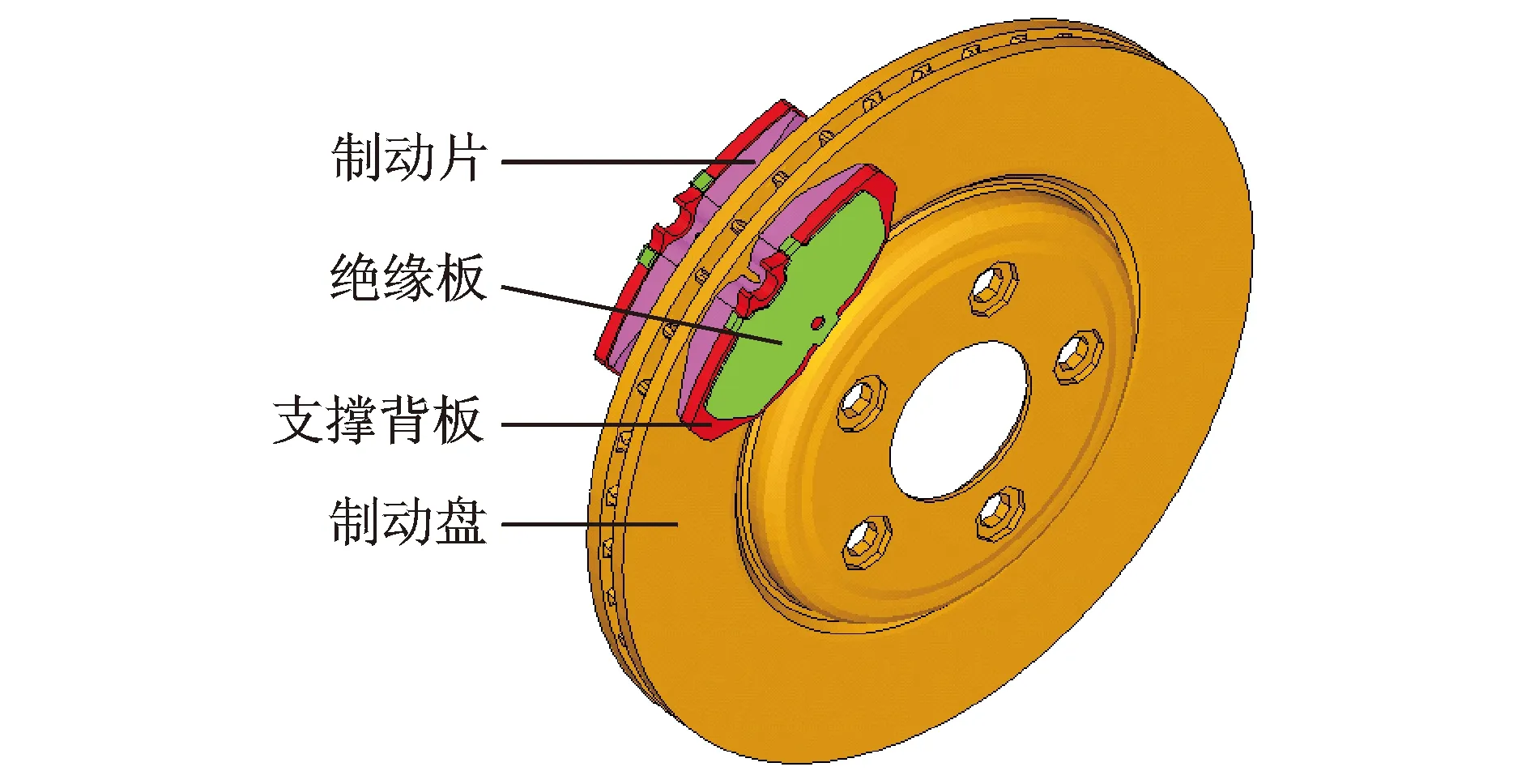
图1 盘式制动器简化结构

制动器工作时，系统引入了摩擦力，导致系统为一个耦合系统，其振动方程可以表示为[9]

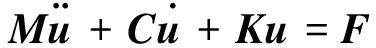
(1)

式中M，C，K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；u为振动位移向量；F为制动盘和制动片接触表面的摩擦接触力，其可以简化为以下线性形式[9]

F=Kfu

(2)

式中Kf为摩擦接触刚度矩阵。将式(2)代入式(1)，可得

(3)

由式(3)可以看出，由于摩擦力的存在导致了系统刚度耦合，系统的刚度矩阵不对称。刚度矩阵不对称则意味着特征矩阵不对称，而不对称矩阵的特征值在一定条件下是复数，即系统各阶模态频率和模态振型都是复数。

式(3)的解可写成如下形式

u=φest

(4)

式中φ为特征向量，s为特征值。上式代入式(3)，可得

(s2M+sC+(K-μKf))φ=0

(5)

对该方程求解可得特征值和特征向量。

系统第i阶特征值可表示为

si=αi+jβi

(6)

式中αi为第i阶特征值的实部，是系统的阻尼系数；βi为第i阶特征值的虚部，是系统的自然频率。

与第i阶特征向量对应的系统响应可表示为

ui=φieαitcosβit

(7)

参考文献[5]，定义系统第i阶阻尼比

(8)

如果阻尼比为正，阻尼消耗能量，系统是一个典型的振动衰减系统，系统是稳定的。如果阻尼比为负，阻尼不耗散能量反而向系统中馈入能量，形成自激振动现象，并使得系统随时间推移而放大振动，从而可能形成噪声。因此可以根据系统的阻尼比判断系统的稳定性，预测出现制动噪声的趋势。

2 随机参数制动器的稳定性研究

2.1 随机参数下特征值的统计特性

(9)

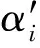
(10)

(11)

参考文献[10]，本文中取ζc=-0.01。

制动器系统的稳定程度取决于阻尼系数αi和阻尼比ζi的概率分布。

2.2 随机参数下系统特征值的灵敏度

为研究随机参数对系统特征值的影响，与确定性灵敏度分析对应，本文针对特征值引入灵敏度分析。特征值实部的灵敏度表示为

(12)

式中αi为第i阶特征值的实部，是系统的阻尼系数；Sαi为灵敏度，为随机分布参数；xm为第m个随机参数。类似地，阻尼比对随机参数的灵敏度为

(13)

进行灵敏度分析时，需要先对变量进行标准化，以消除量纲、变量自身变异和变量数值大小的影响。将变量标准化为

(14)

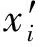
2.3 随机参数下制动器稳定性分析

本文将随机参数引入到汽车盘式制动器稳定性研究中，用随机参数对制动器的不确定性进行描述，提出了一种随机参数汽车盘式制动器的稳定性分析方法。其主要步骤为:

(1)基于制动器系统的有限元模型，在随机参数不确定空间范围内进行试验设计，求出系统对应各组样本点的各阶特征值；

(2)选择特征值实部大于0的特征值为目标特征值，建立系统目标特征值的参数化响应面模型；

(3)采用蒙特卡洛方法对目标特征值的随机特性和目标特征值对随机参数的灵敏度进行分析；

(4)根据目标特征值的随机特性和目标特征值对随机参数的灵敏度研究各参数对制动器系统稳定性的影响，并从可靠性的角度提出提高系统稳定性的改进方案。

本文方法的具体分析流程如图2所示。

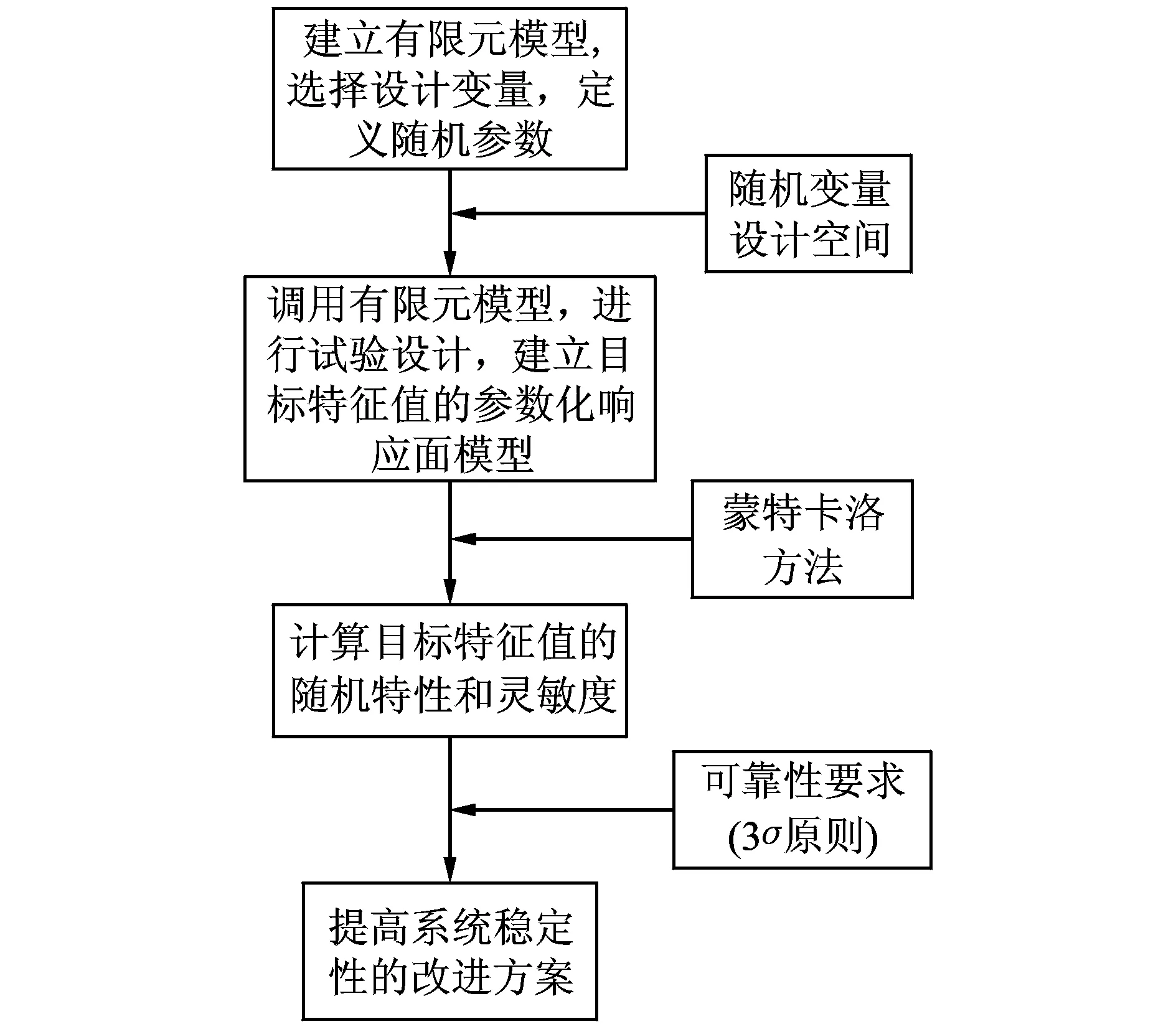
图2 随机参数制动器的稳定性分析流程

3 算例研究

3.1 汽车盘式制动器参数化模型

汽车制动器是由多个部件组成的系统，以盘式制动器为研究对象，主要的部件有制动盘、制动片、支撑背板、绝缘板、卡钳、分泵和油管等。由于制造精度和加工工艺的影响，部件的几何尺寸和系统的作用载荷等参数存在一定的波动性，具有不确定性。

为了减少计算工作量，同时又能真实准确地模拟制动器的振动特性，本文利用Altair. Hypermesh软件建立了某型轿车的制动器有限元简化模型，如图3所示。

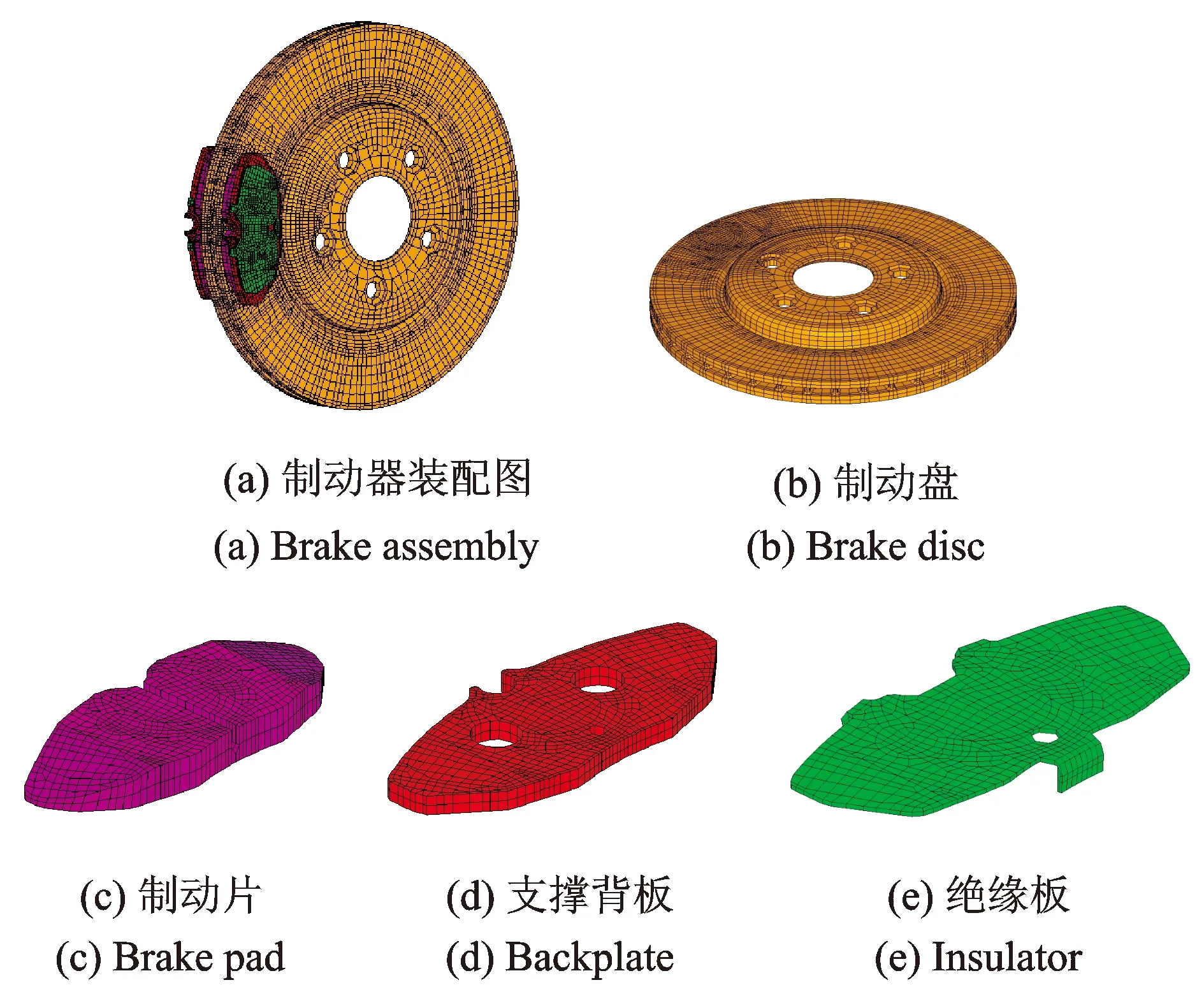
图3 制动器有限元模型

简化模型由制动盘、制动片、支撑背板和绝缘板四部分组成，共划分成26 125个实体单元，37 043个节点，其中六面体单元(C3D8)数量为25 041，五面体单元(C3D6)数量为1 084，制动片与制动盘之间为摩擦接触面，整个系统为一个摩擦耦合系统。将定义好边界条件和工况的有限元模型提交ABQUS/Standard，即可求解系统复域的各阶特征值。

文献[5]的研究表明，在盘式制动器系统中，摩擦系数x1、制动压力x2、制动片厚度x3、制动盘厚度x4和支撑背板厚度x5这些参数都与系统的稳定性有关，因此本文采用拉丁超立方试验设计方法在这些参数组成的取值范围空间内采样[11]。拉丁超立方试验设计方法是一种用来安排多因素试验的方法，常用于大型采样设计空间。它可以用较少的试验次数提供更多的信息，降低试验误差。

工程实际中常用正态分布来描述零部件几何厚度和边界载荷的分布情况，假定所有随机变量均服从正态分布，其取值情况如表1所示。

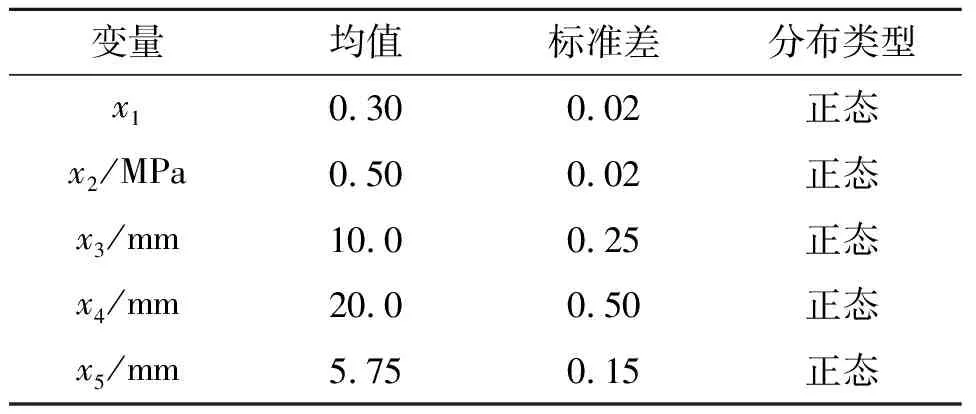
表1 随机变量的参数值及分布类型

抽取50组样本点代入到制动器系统有限元模型中进行计算，求出0～16 kHz范围内的系统特征值及相应的阻尼比，发现系统对应各组样本点的第7阶特征值实部均大于0，为不稳定特征值；各样本点还在其他阶次上出现不稳定特征值，但其阻尼比都远比第7阶阻尼比小，因此本文将第7阶特征值作为目标特征值进行研究。某一样本点下，系统0～16 kHz范围内的所有特征值分布如图4所示。

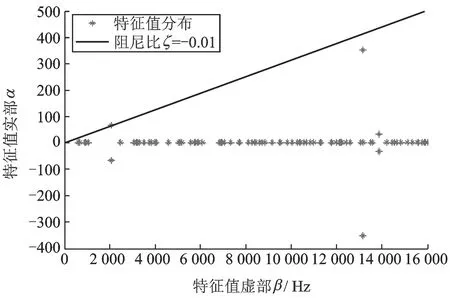
图4 某样本点下系统的特征值分布

在上述试验设计的基础上，建立第7阶特征值的参数化模型。基于二阶多项式响应面模型建立的第7阶特征值实部和虚部的近似表达式如下

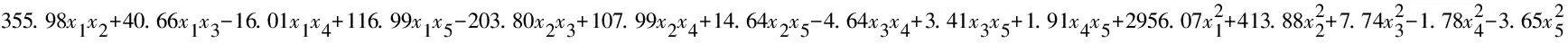
(15)

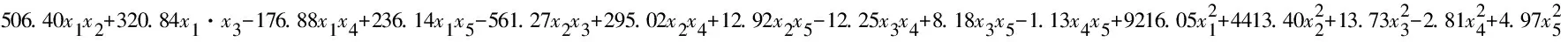
(16)

式中α7，β7分别为第7阶特征值的实部和虚部；xi(i=1,2,3,4,5)为系统变量。

根据文献[11]的方法对上述响应面模型进行显著性分析，由F检验结果可知响应面模型的不可靠概率小于1%，与真实有限元模型的逼近程度高，能够用于后续分析研究。

3.2 特征值的统计特性

蒙特卡洛法，也称统计模拟方法，作为求解工程问题的重要方法之一，对仿真问题的维数不敏感，且不受任何假设的约束，可通过大量的随机抽样获取较高的求解精度，具有很强的适用性[12]。

使用蒙特卡洛法迭代104次，可得系统第7阶特征值的概率分布如图5所示。

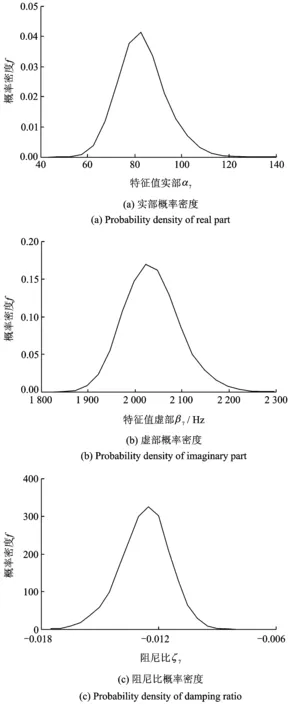
图5 第7阶特征值的概率分布

计算得第7阶特征值的均值、标准差和分布区间如表2所示。

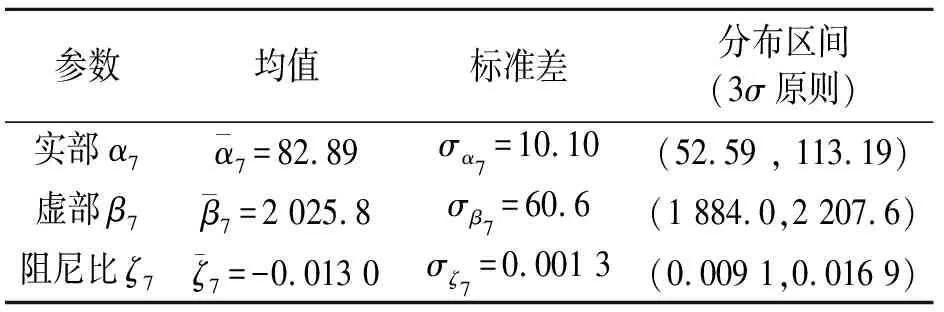
表2 第7阶特征值计算结果

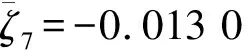
3.3 特征值概率灵敏度

为了考察随机参数变量对目标特征值的影响，图6给出了第7阶特征值对各变量的灵敏度分布。

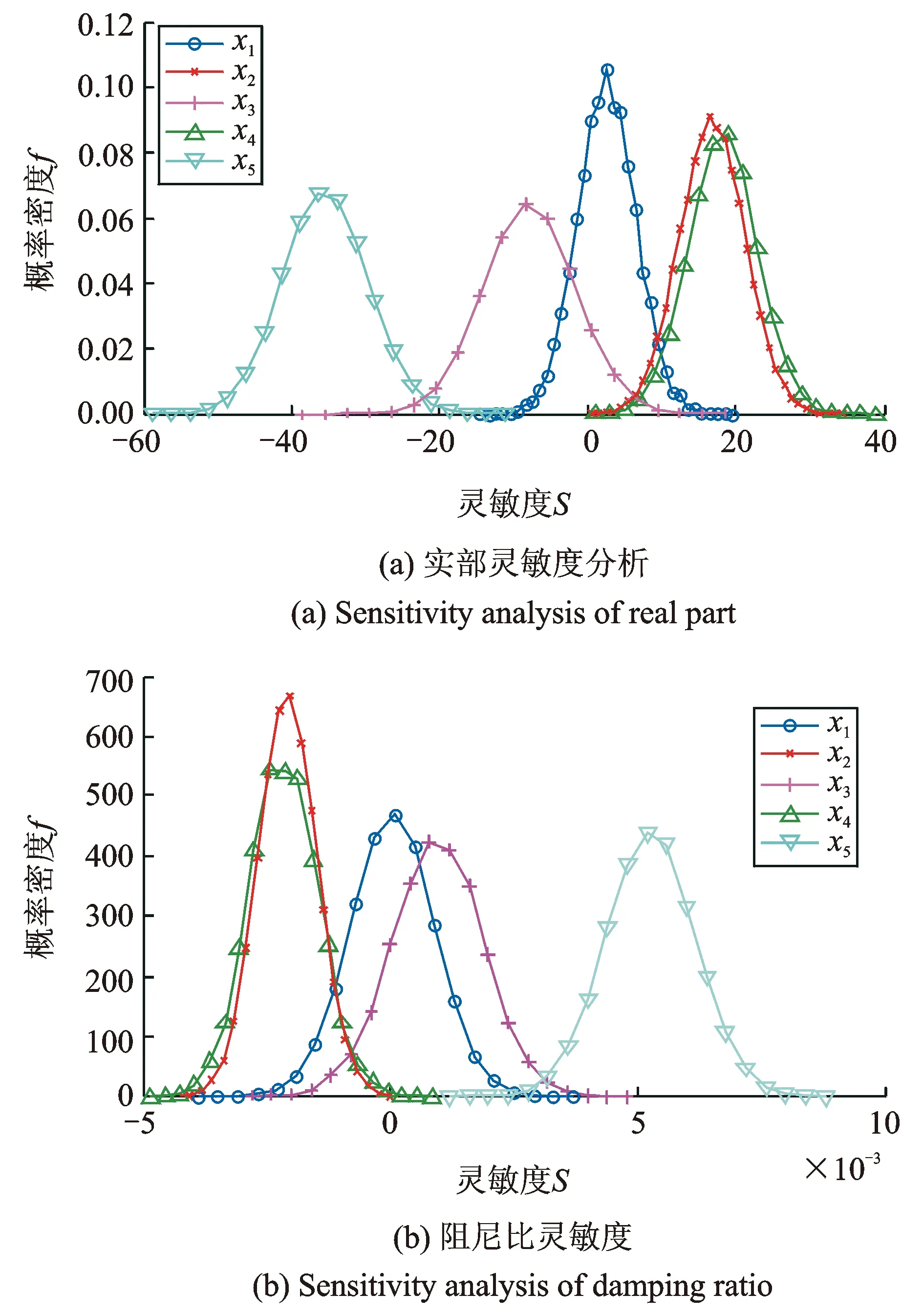
图6 目标特征值的灵敏度分析

由图6(a)可知:

(1)从区间分布上看，特征值实部对支撑背板厚度变量x5的灵敏度分布在恒为负值的区间中；对制动压力变量x2和制动片厚度变量x4的灵敏度分布在恒为正值的区间中；对摩擦系数变量x1和制动盘厚度变量x3的灵敏度分布在正负结合的区间中，关系较复杂。

(2)从分布均值上看，特征值实部对支撑背板厚度变量x5的灵敏度最高，x2和x4次之，x1和x3最低。

对图6(b)分析可得出类似的结论。

算例中目标特征值实部恒为正值，理论上应该将其消除或者负值化，以从根本上提高稳定性，但是这样处理成本往往较高，工程上常通过减小实部的大小，将特征值在复平面上左移，以降低其不稳定性。结合前面的灵敏度分析可知，通过修改支撑背板的厚度以提高支撑刚度是最有效和直接的方法，这与已有文献[13]的研究结论是相吻合的。

3.4 系统稳定性的提高和验证

为了考察支撑背板的厚度对目标特征值的影响，选取一系列x5均值，其他参数均取为初始值，重新构建适用于最大设计空间的响应面模型，求出对应的目标特征值，结果如图7所示。

图7 不同支撑背板厚度下系统的目标特征值分布

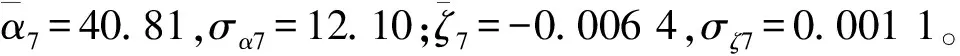
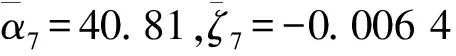
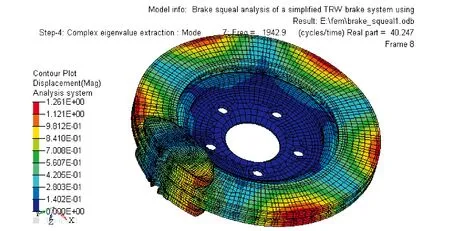
图8 第7阶复模态有限元分析结果

为了验证分析结果的有效性，在其他参数均取初始值的情形下，对比x5=7.5 mm和x5=5.75 mm两种取值下系统在0～16 kHz范围内的复特征值分布，结果如图9所示。从图中可以看出改进设计后系统特征值分布更集中，阻尼比值更小，系统稳定性更高。

图9 改进前后系统的复特征值分布对比

4 结 论

(1)本文将随机参数引入到汽车盘式制动器稳定性研究中，使用随机参数对制动器的不确定性进行描述，将响应面法与有限元复特征值技术相结合，实现了制动器稳定性研究模型的参数化，大大提高了分析效率。

(2)在系统参数正态分布假设下，研究了某型车浮钳盘式制动器系统特征值的概率统计特性，通过对设计参数的概率灵敏度分析，发现通过修改支撑背板的厚度变量，提高支撑刚度可有效提高系统的稳定性。

参考文献:

[1] Dai Y， Lim T C. Suppression of brake squeal noise applying finite element brake and pad model enhanced by spectral-based assurance criteria[J]. Applied Acoustics，2008，69(3)：196—214.

[2] Fritz G， Sinou J J， Duffal J， et al. Effects of damping on brake squeal coalescence patterns application on a finite element modal[J]. Mechanics Research Communication，2007，34(2)：181—190.

[3] Nack W V. Brake squeal analysis by finite elements[J]. International Journal of Vehicle Design，2000，23 (3/4)：263—275.

[4] 宿新东，管迪华.利用子结构动态特性优化设计抑制制动器尖叫[J].汽车工程，2003,25(2)：167—170.Su Xindong， Guan Dihua. Reduction of brake squeal using substructure dynamic characteristics optimization[J]. Automotive Engineering，2003，25(2)：167—170.

[5] Liu P， Zheng H， Cai C. Analysis of disc brake squeal using the complex eigenvalue method[J]. Applied Acoustics，2007，68(6)：603—615.

[6] Oberst S， Lai J C S. Statistical analysis of brake squeal noise[J]. Journal of Sound and Vibration，2011，330 (12)：2 978—2 994.

[7] Sarrouy E， Dessombz O， Sinou J J. Piecewise polynomial chaos expansion with an application to brake squeal of a linear brake system[J]. Journal of Sound and Vibration，2013，332(3/4)：577—594.

[8] Myers R H， Montgmery D C， Anderson C M. Response surface methodology-process and product optimization using designed experiment[M]. New York：Wiley Publishers，2009.

[9] Junior M T， Gerges S N Y， Jordan R. Analysis of brake squeal noise using the finite element method[J]. Applied Acoustics，2008，69(2)：147—162.

[10] 吕辉，于德介，谢展，等.基于响应面法的汽车盘式制动器稳定性优化设计[J].机械工程学报，2013，49(9)：55—60.Lü Hui， Yu Dejie， Xie Zhan, et al. Optimization of vehicle disc brakes stability based on response surface method[J]. Chinese Journal of Mechanical Engineering，2013，49(9)：55—60.

[11] Papilla M. Accuracy of response surface approximations for weight equations based on structural optimization[D]. Gainesville：University of Florida，2001.

[12] Zhang H， Mullen R L， Muhanna R L. Interval Monte Carlo methods for structural reliability[J]. Structural Safety， 2010，32(3)：183—190.

[13] Nouby M， Mathivanan D， Srinivasan K. A combined approach of complex eigenvalue analysis and design of experiments (DOE) to study disc brake squeal[J]. International Journal of Engineering， Science and Technology，2009，1(1)：254—271.