基于混合统计模型的DNA序列压缩算法*

孙季丰 仝雪珂 谭丽

(华南理工大学电子与信息学院，广东广州510640)

DNA序列数据在诸多领域具有重要的研究和应用价值，如医学、遗传科学等.以获取DNA序列数据为目标的生物测序工程近年来得到广泛重视.随着各种测序项目的展开，DNA序列数据以指数规模急剧增长，在有限的存储资源内有效存储和应用成本日益增大，因此需对DNA序列进行有效的压缩.由于DNA序列的特殊性，普通压缩算法效果并不理想，需要使用专门的算法进行压缩［1］.

目前主要有两类专门针对DNA序列数据的压缩算法.第1类基于替代的压缩算法在过去是主流算法，自1993年Grumbach等［2］学者首次提出Bio-Compress算法后，相继出现 GenCompress算法［3］、DNACompression算法［4］、DNAPack算法［5］、GeNML算法［6］、在线DNA序列的水平与垂直压缩［7］、使用基于压缩算法的近似重复和提供随机存取能力的系统［8］、LSBD算法［9］、BioLZMA算法［10］以及改进的游程编码算法［11］等基于替代的压缩算法.第2类基于统计信息的压缩算法只是其得不到满意结果的补充.Allison等［12］在1998年提出ARM算法，Loewenstern等［13］在1999年提出CDNA算法，两种算法在当时都产生了比替代算法更好的压缩率.Korodi等［14］在2007年提出基于NML的算法，Cao等［15］在2007年提出专家模型算法(XM算法).NML算法和XM算法可单独处理DNA序列，使统计信息压缩算法的应用效果有了显著提高.

文中主要研究第2类基于统计信息的数据压缩算法.基于XM算法理论，Pinho等［16-18］使用有限上下文模型进行序列的统计压缩，实验结果表明，改进后的算法能产生更好的压缩率.不同有限上下文模型的区别在于模型阶数不同，鉴于其特点，文中将每一阶模型改为含有某特定规律的多个模型的混合，可称为混合统计模型.另外，文献［16-18］中所述算法并未应用于标准DNA序列集，因此不具备普遍意义上的一般性.因此，基于XM算法理论，文中使用有限上下文混合统计模型，对标准DNA序列集进行算术编码统计压缩;并将文中算法与基于统计信息的当前较先进的XM算法以及其他压缩算法进行了比较.

1 DNA序列的压缩

DNA序列数据的压缩通过两个步骤完成，首先使用描述的模型完成序列的统计概率计算，其次使用所得概率计算结果进行算术编码压缩.

1.1 DNA序列的概率统计模型

文中使用的概率统计模型基于XM算法，提出的混合统计模型代替XM算法中使用的模型，应用于XM算法，进行序列符号的统计概率计算.

1.1.1 基本XM算法描述

首先基于已知符号的统计情况预测每一个符号位的概率分布，而后进行编码来压缩符号.预测概率需要设置专门的模型，XM算法结合使用少量复制和反相模型，提供了一个将各种模型混合使用预测符号出现概率的基本原理.

统计n位后，模型θk(k∈E)预测第n+1位符号的概率为［15］p(xn+1|θk，x1，2，…，n).其中θk代表使用的不同模型，k为模型的阶数(θ2即2阶该模型)，E为算法使用的模型阶数集合.令 x1，2，…，n=x1x2…xn.基于贝叶斯平均，混合使用不同阶数模型进行预测［15］:

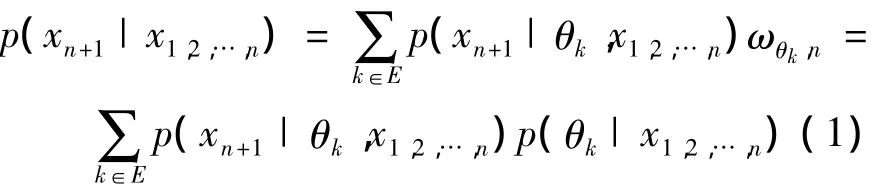
权重ωθk，n为统计n位后k阶模型θk估计xn+1出现概率的参与度，依照分析可由p(θk|x1，2，…，n)表示.评估模型的使用价值，需要使用距离当前位置最近的历史序列.当前位置前的20个符号值能够得到最好实验结果的窗口值，因此，XM算法取窗口值w=20.

1.1.2 基本有限上下文模型

有限上下文模型描述如下(以4阶为例)［16］.

图1中输出结果概率一般由下式所得［17］:

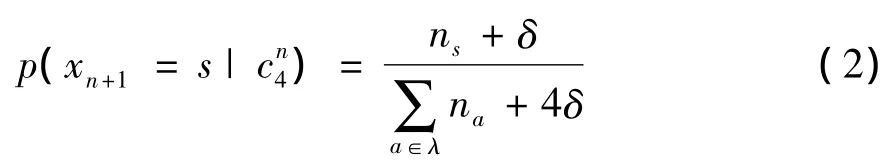
式(2)分母中∑na为计算到第n+1位时，前n位序列中上下文序列中(如图1中ACAG)出现的次数，分子中ns为上下文序列后出现某符号s(如G)的次数，δ控制分配给未知事件的可能性，在阶数小时默认为1.此式含义为计算某上下文序列(如ACAG)后一位出现某符号(如G)的概率，此式亦为公式(1)中当θk使用有限上下文模型时概率p(xn+1|θk，x1，2，…，n)的计算结果.

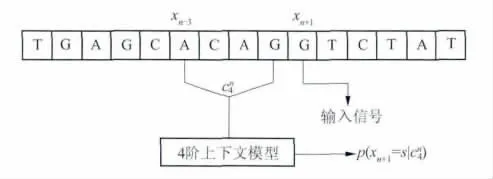
图1 4阶上下文模型统计概率计算Fig 1 Statistical probability calculation of 4-order context model

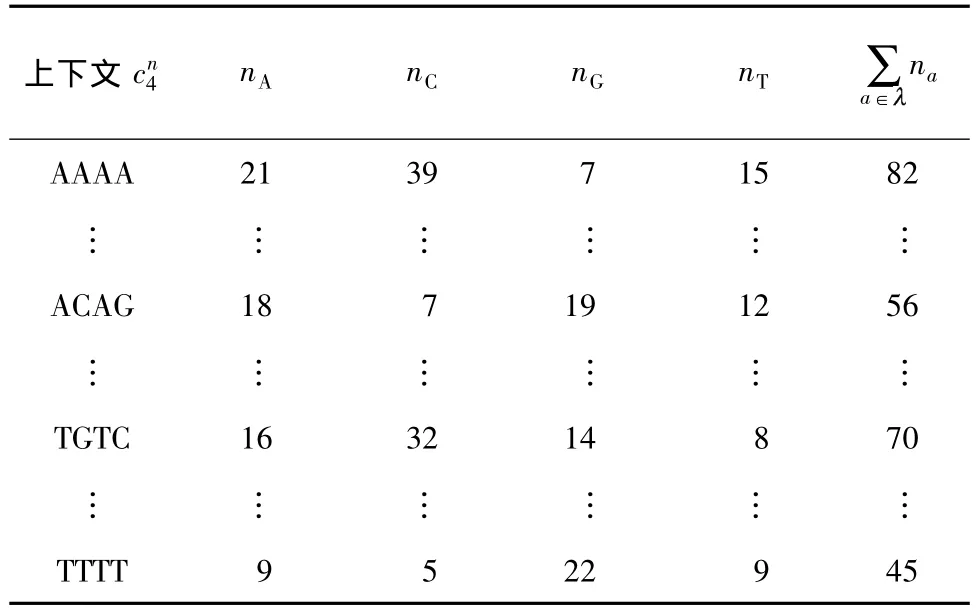
表1 上下文模型统计结果Table 1 Statistics results of context models

文中总结此模型的概率求解特点如下:①图1所示的统计表是实时更新的;②当前位的统计概率基于更新到当前位置的统计表;③可设置不同的阶数，某一位置符号针对不同阶数存在不同的统计表和相应的统计概率.

将有限上下文模型做为XM算法中模型θk，即k(k∈E)阶模型θk使用k阶有限上下文模型，进行统计概率计算.

1.1.3 各阶上下文模型的贡献权重

(1)权重求解

使用贝叶斯理论估计式(1)中权重ωθk，n的值，计算基于下式［15］:

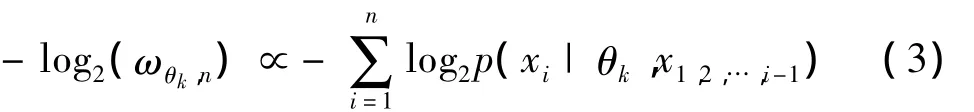
式(3)代表正相关比例关系.k阶模型θk用k阶有限上下文表示，令ωk，n为k阶有限上下文模型应用于k阶模型θk所对应的ωθk，n，重新表达式(3):

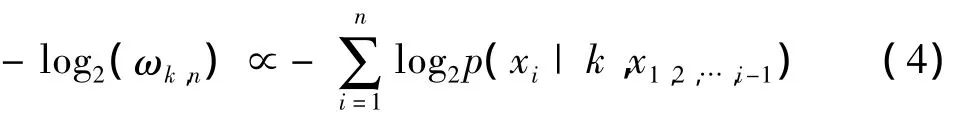
式(4)右边是编码xi(i=1，2，…，n)共消耗的二进制比特数，其中概率部分求解同式(2).式(4)右边正比于权重值ωk，n，根据其所求各阶模型的权重比例以及∑ωk，n=1，即可求出各阶模型的权重值.由于上下文模型所得概率是实时更新的，因此所得权重也是实时更新的，即每运算到一位，都要计算当前位各阶模型的贡献权重.

至此求出上下文模型用于模型θk所需的统计量:各阶模型的符号实时统计概率和贡献权重，以此综合计算符号的实时统计概率.其中，贡献权重的求解基于相应阶数模型的符号实时统计概率.

(2)k阶上下文模型权重

有限上下文模型并不适用于数据序列的任意区域，而是依赖距离当前处理符号位最近的区域.借鉴学者Armando J.Pinho的基于遗忘策略的递归关系，可得较好的权重预测结果.

为式(4)引入参量γ［18］:

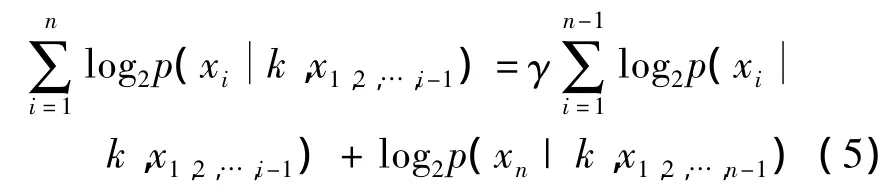
式(5)中参量γ能够使符号的概率估计值受最接近当前位置的符号影响更大，较符合实际情况，因此能够产生更准确的预测.

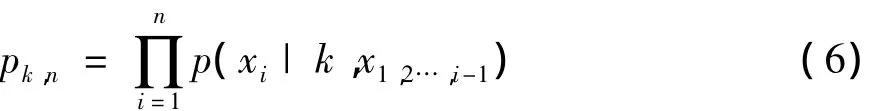
定义［18］:重新表达式(5)［18］:

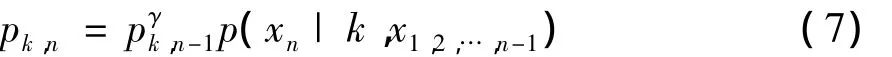
最终可得［18］

上式仅为所求得的权重比例，再根据∑ωk，n=1，即可求得改进的权重值.参量γ的选取须进行实验，根据最优结果值(能够使标准DNA序列产生最小的信息熵)进行选取.

1.1.4 混合统计模型

针对具体某一阶上下文模型提出改进模型.以4阶模型为例，原有限上下文模型的上下文Ci是4个连续符号序列(如ACAG).现将4个连续符号序列改为每2个连续符号取一个符号(隔一位取位模型)和每3个连续符号取一个符号(隔两位取位模型)来进行上下文模型的选择.如图2所示.

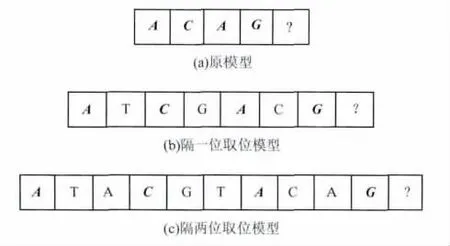
图2 原模型以及两种改进模型Fig 2 Original model and two improved models

隔位取位模型处理更多的历史数据，有助于取得更准确的预测概率.在原模型中，预测当前位符号的概率要处理4位历史数据(见图2(a)所示);而在隔一位取位模型中，需要处理7位历史数据(如图2(b)所示)，将7位数据隔一位取位，得到加粗表示的四位符号，作为隔一位取位模型的4阶上下文，非加粗表示的数据略去不用;同理，图2(c)所表示的隔两位取位模型需要处理10位历史数据，将加粗表示的4位符号作为此改进模型的4阶上下文，非加粗表示的数据略去不用.

为使用更多历史数据，可继续生成隔三位取位模型，隔四位取位模型，…;文中只采用了原模型、隔一位取位模型与隔两位取位模型.后续生成的一系列改进模型，可用做后续研究.

使用连续取位或隔一位取位、隔两位取位，并没有相关的先验概率.故使用此3种模型，则分别取它们的概率各为1/3，将同一阶数的3种取位模型混合使用，作为文中所提出的混合统计模型.将混合统计模型应用于XM算法.

使用4阶原模型预测序列第n位出现符号A的概率用P4a1(n)表示，使用隔一位、隔两位取位模型预测的概率分别为P4a2(n)、P4a3(n)，由于无先验概率，得到

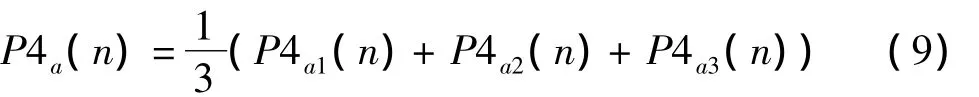
P4a(n)为4阶混合统计模型在第n位上出现符号A的概率，同理可计算出P2a(n)、P6a(n).依XM算法原理，应用模型都要确定模型阶数集合(包括原模型、混合统计模型)，在文中选择k=2、4、6，即E={2，4，6}.可根据1.1.3部分实时计算出使用2、4、6阶模型的权重ω2(n)、ω4(n)、ω6(n).据此可由XM算法部分公式(1)得

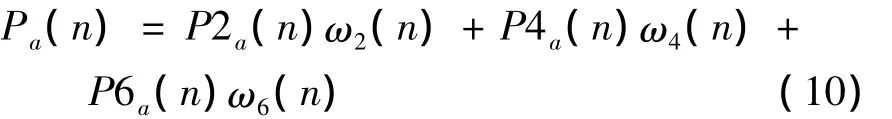
上式为第n位出现A的概率.同理可得此位出现C、G、T的概率分别Pc(n)、Pg(n)、Pt(n)，并存在

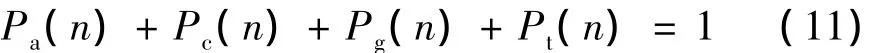
这即为进行算术编码计算实时编码比例所需的4种符号概率.当编码序列长度为N时，需求解n在1～N中所有符号位上的4种符号概率.

1.2 DNA序列编码

混合统计模型应用于XM算法，即可求出算术编码的实时编码比例，这既不同于传统算术编码中已知固定编码比例，也不同于自适应算术编码中编码比例的实时求出，而是已求得的不同符号位置的不同编码比例，以此为基础进行算术编码.

计算到第n位，对ACAG进行算术编码:

(1)1.1.4部分实时计算出第n位上4种符号概率Pa(n)、Pc(n)、Pg(n)、Pt(n)，进一步转化如图3所示.

图3 第n位实时编码比例Fig 3 Real-time encoding proportion in the n bits

其中整个线段长度代表全部概率1，计算PA(n)、PC(n)、PG(n)和PT(n)，使得:

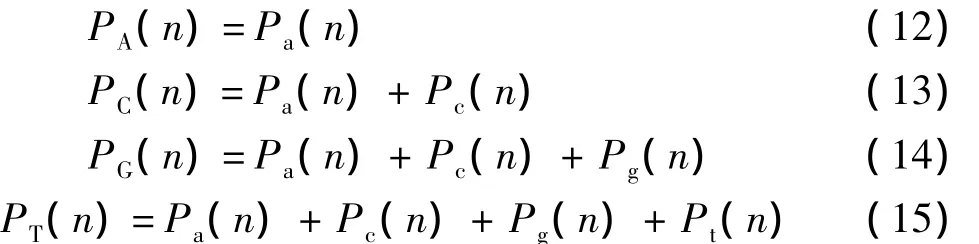
事实上，由于Pa(n)+Pc(n)+Pg(n)+Pt(n)=1，故PT(n)=1.第n位为符号A，则编码取概率区间0～PA(n).

(2)再根据实时计算的第n+1位出现的4种符号概率Pa(n+1)、Pc(n+1)、Pg(n+1)、Pt(n+1)进行在区间0～PA(n)上的转化，如图4所示.

图4 第n+1位实时编码比例Fig 4 Real-time encoding proportion in the n+1 bits

计算PA(n+1)、PC(n+1)、PG(n+1)和PT(n+1)，使得:

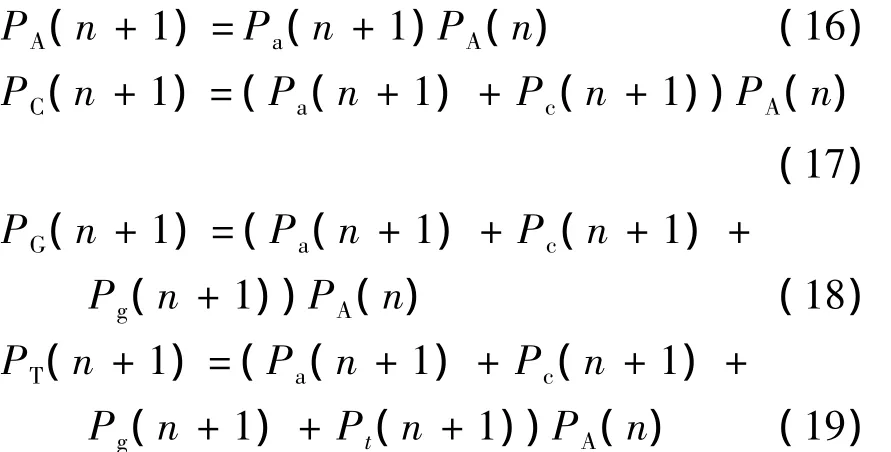
又由于Pa(n+1)+Pc(n+1)+Pg(n+1)+ Pt(n+1)=1，故PT(n+1)=PA(n).第n+1位为符号C，则编码取概率区间PA(n+1)～PC(n+1).

(3)下面继续进行的编码步骤同上，直到编码完成得到一个区间，取区间中小数表示此段序列的编码值.以此值编码此一系列符号.所得小数数值由数字0～9表示，以下分析将其转换为二进制表示.

在没有先验概率的前提下，首先假设编码后10个数字0～9出现的概率是相同的.由于23＜10＜24，所以表示每一个数字的二进制符号位数在3～4之间.三位二进制数表示值有000、001、010、011、100、101、110、111，共8个.为使增添的四位二进制数在解码时不与三位二进制数相混淆.去掉000，增添0000和 0001;去掉 111，增添 1110和1111.则10个数字可以由001、010、011、100、101、110、0000、0001、1110、1111表示.在解码时，先观察前3个符号位，当都相同(为000或111)时，则使用前4个符号位对数字进行解码.当不全相同时，则使用3个符号位对数字解码.则可一一对应解码数字0～9.编码每一个数字所需的平均二进制符号位为

(3×6+4×4)/10=3.4.

(4)随着编码位数的增加，所需的小数位数也在逐步增加，因此需要设定一个固定的长度，在计算机软件的计算精度范围以内，经试验取25最为合适.即每次取25位进行算术编码，二进制转换.

混合统计模型应用于XM算法的流程图如图5所示.

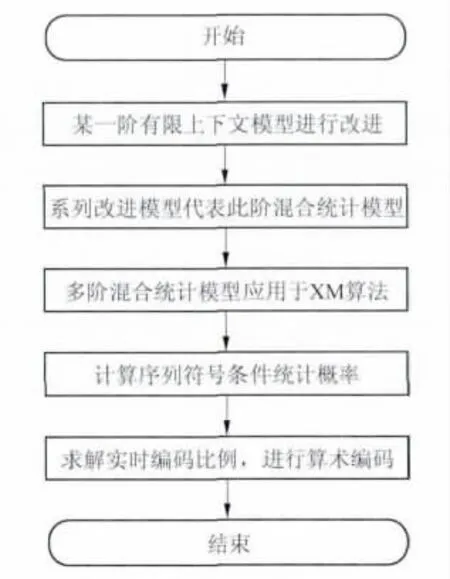
图5 完整算法流程图Fig 5 Flowchart of full algorithm

2 实验数据与结果分析

2.1 参数设置

1.1.2 部分上下文模型由序列第1位开始进行实时统计.在初始位，令表1中数据全部为零;各符号(A、C、G、T)出现的初始概率均为1/4;模型阶数集选取E={2，4，6};各阶模型初始贡献权重相同(文中令ω2(1)、ω4(1)、ω6(1)均为1/3);式(2)中δ=1.

2.2 结果与分析

实验选取美国国家生物技术信息中心(NCBI)收集的DNA序列数据.为进行对照，将算法应用于DNA压缩领域文献中最常使用的标准DNA序列集.

压缩之前，分析1.1.3部分的权重改进引入的参数γ.经验获得的γ在0.970～0.998之间.混合统计模型所得标准DNA序列符号平均信息熵见表2.

表2中数据为表示一个碱基符号所需的二进制比特数(单位为信息熵单位Bits Per Base，缩写为BPB)，加粗数据为使用不同参量值所得最优值(最小信息熵).当γ取0.995时，能够取得在各标准序列上的最小信息熵，故γ=0.995.

表3示出了应用于标准DNA序列集时，使用原模型和文中提出的混合统计模型进行压缩的结果比较(原模型与混合统计模型均需混合使用3个阶数有限上下文模型，阶数k分别为2、4、6).显然有:混合统计模型比原模型需要更小的二进制比特表示(9段序列使用混合统计模型显示更好的压缩效果)，因此混合统计模型能够显示更好的压缩效果.

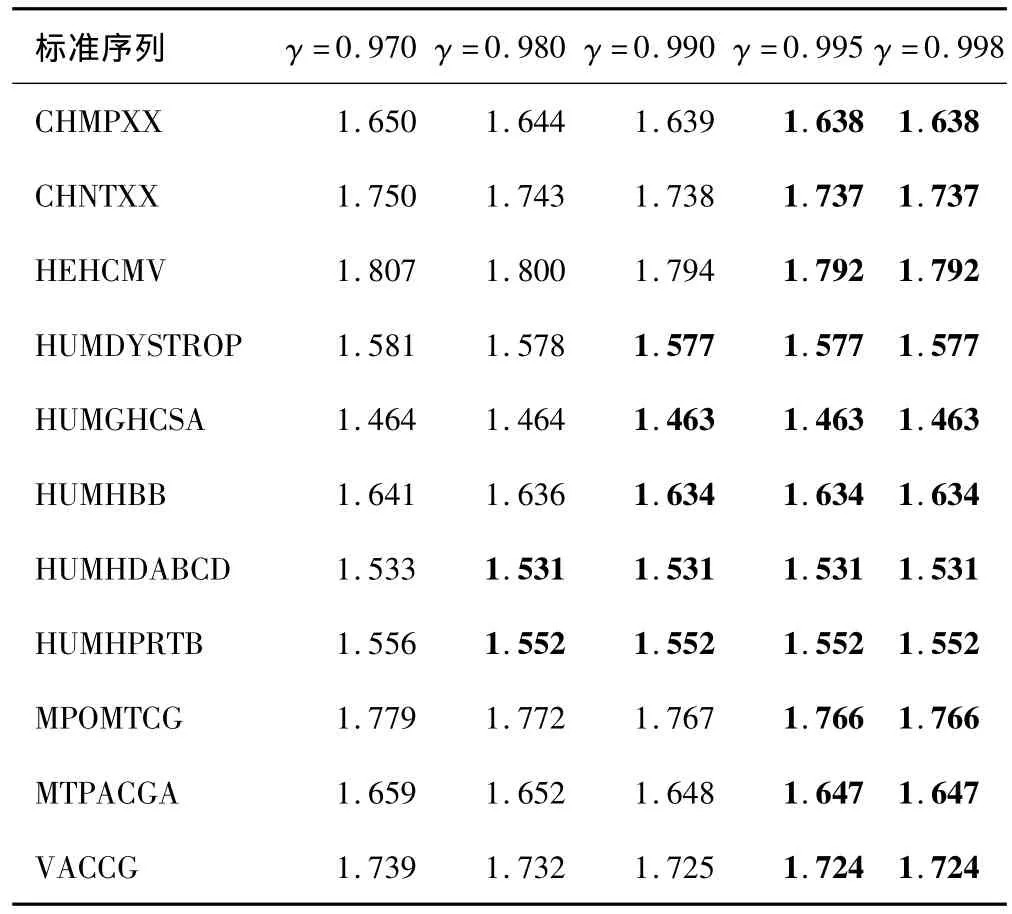
表2 使用不同参量值在标准序列上的信息熵Table 2 Information entropies of the standard sequences by using different parameter values BPB

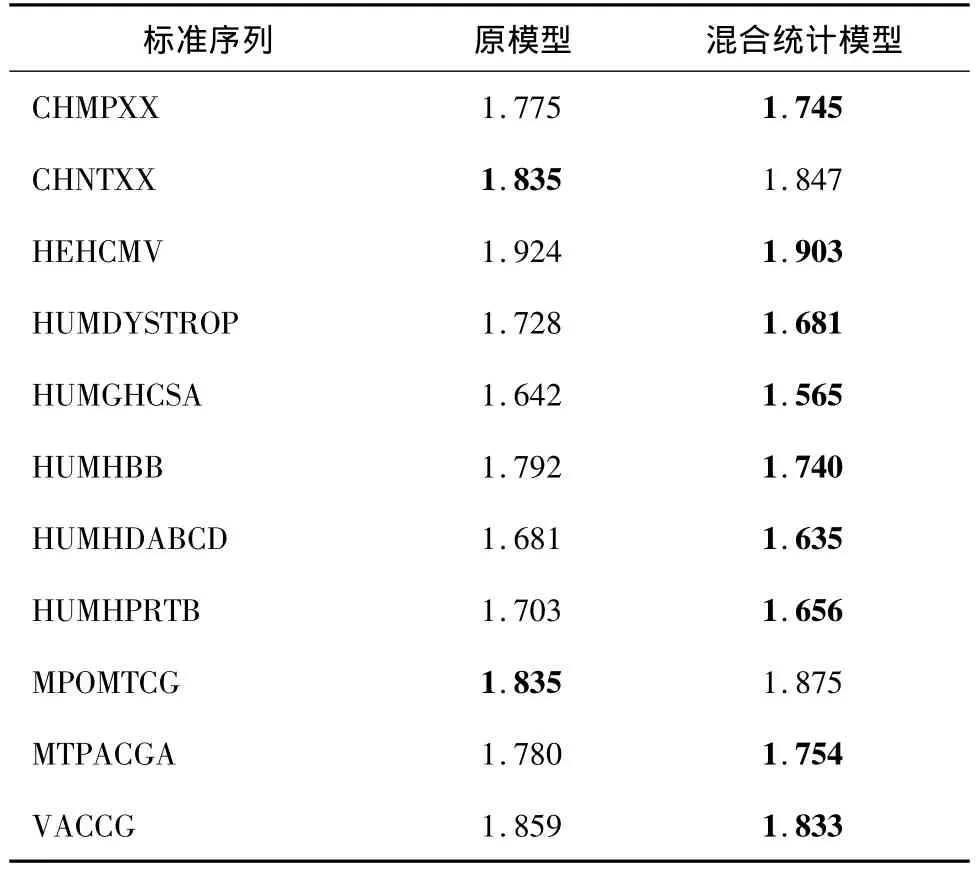
表3 不同模型使用方式在标准序列上的压缩率Table 3 Compression ratios in the standard sequences by using different models BPB

表4示出了文中提出的混合统计模型压缩算法同其他应用于DNA序列压缩算法的比较.文中提出的多阶混合统计模型和一系列用于对照的压缩算法相比更有优势.在序列 CHMPXX、CHNTXX、HUMGHCSA上，XM算法产生最优压缩结果.在序列HUMDYSTROP、HUMHBB、HUMHDABCD、HUMHPRTB、MPOMTCG和MTPACGA上，混合统计模型产生最优压缩结果.在序列 VACCG上 DNACompress算法有最好的压缩比，序列HEHCMV上是DNAPack算法.

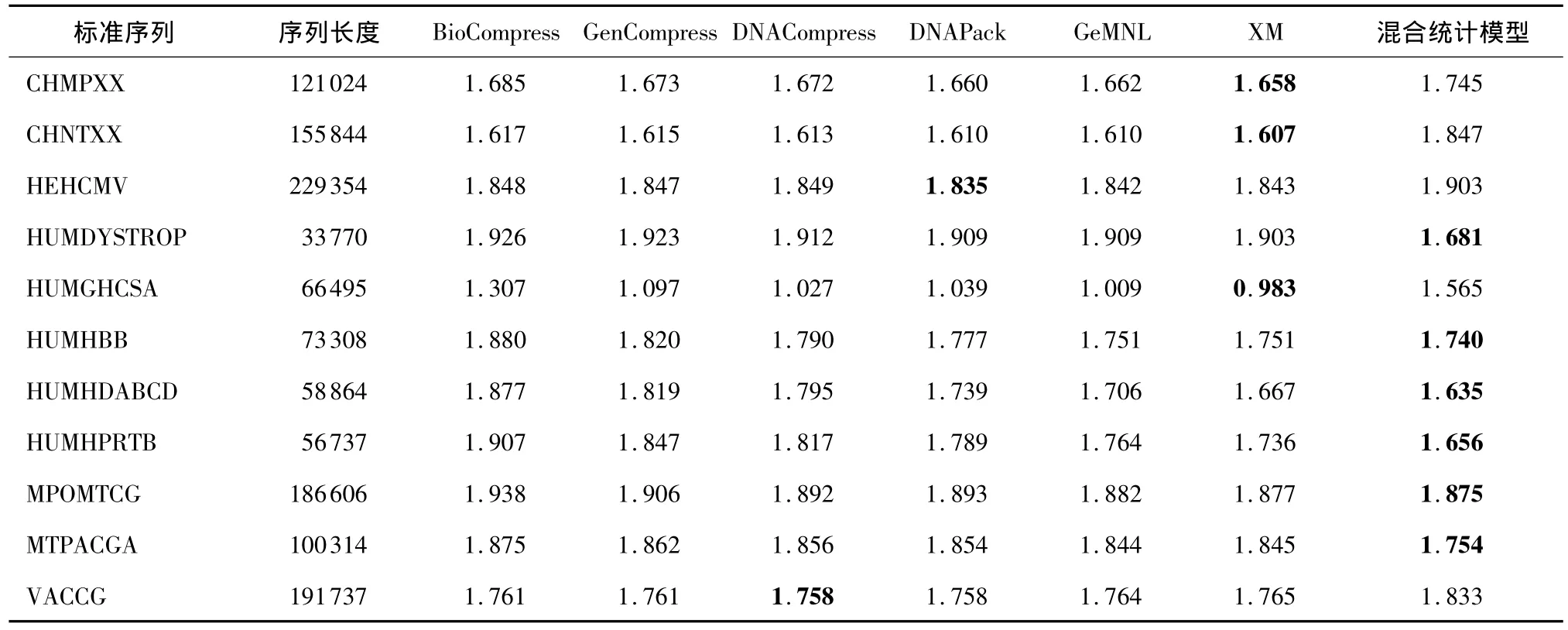
表4 不同压缩算法在标准序列上的压缩率Table 4 Compression ratios of compression algorithms in the standard sequences BPB

根据数据分析，和基于统计信息的当前较先进的XM算法相比，文中所使用的混合统计模型能够产生更好的压缩效果.对于使用XM算法压缩效果较差的标准DNA序列，混合统计模型算法表现出更好的压缩效果，能够弥补XM算法应用于一些序列的不足，完成进一步压缩。

将文中算法压缩人类染色体的结果与XM算法进行对比(见表5).实验结果表明，文中算法压缩效果比XM算法差，未彰显算法优势，因此仅在此列出两条染色体(FASTA格式)的对比结果(序列下载链接为 http:∥ www.ncbi.nlm.nih.gov/nuccore/ 1577282 28?report=fasta和http:∥www.ncbi.nlm. nih.gov/nuccore/157729478?report=fasta).

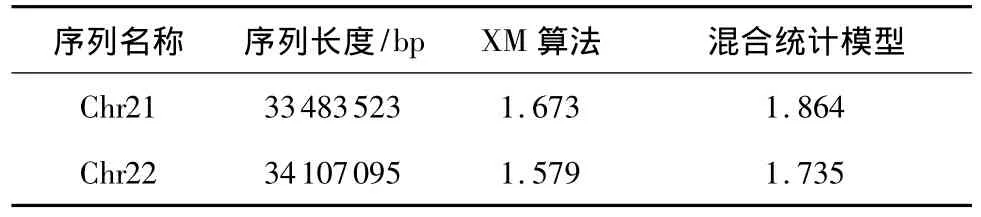
表5 对两条人类染色体的压缩率Table 5 Compression ratios in two Homo sapiens chromosomes BPB

由表5可知:文中提出的算法对人类染色体这类长度超过千万的高通量DNA数据［19-20］的压缩效果有待提高.

3 结语

文中在多个阶数有限上下文模型综合应用的基础上，对每一阶模型进行多种取位的混合，再使用混合模型压缩数据，同原模型进行对比，并同其他一系列经典DNA序列压缩算法(包含当前基于统计理论压缩效果最优的XM算法)进行对照.实验结果表明:改进算法优于其他压缩算法，能够弥补XM算法应用于序列标准DNA集部分数据的不足.但对高通量DNA数据(如人类染色体)的压缩有待提高.

由于混合模型只是原模型与隔一位、隔两位取位模型的未知先验概率的混合使用，因此还可以进行模型的后续改进:①增加新模型的种类，可依据文中的两种取位模型的趋势进一步改进;②统计估计每种模型的应用效果，进一步为其设置使用权重值，此步骤的进行被限制在某一阶模型中.可依据以上提出的两个方向进行进一步研究，分析压缩率.

［1］ 纪震，周家锐，姜来，等.DNA序列数据压缩技术综述［J］.电子学报，2010，38(5):1113-1121. Ji Zhen，Zhou Jia-rui，Jiang Lai，et al.Overview of DNA sequence data compression techniques［J］.Acta Electronica Sinica，2010，38(5):1113-1121.

［2］ Grumbach S，Tahi F.Compression of DNA sequences［C］∥Proceedings of 1993 Data Compression Conference.Snowbird:IEEE，1993:340-350.

［3］ Chen X，Kwong S，Li M.A compression algorithm for DNA sequences and its applications in genome comparison［J］.Genome Informatics Series，1999(10):51-61.

［4］ Chen X，Li M，Ma B，et al.DNACompress:fast and effective DNA sequence compression［J］.Bioinformatics，2002，18(12):1696-1698.

［5］ Behzadi B，Le Fessant F.DNA compression challenge revisited:a dynamic programming approach［C］∥Proceedings of Combinatorial Pattern Matching.Berlin-Heidelberg:Springer-Verlag，2005:190-200.

［6］ Korodi G，Tabus I.An efficient normalized maximum likelihood algorithm for DNA sequence compression［J］. ACM Transactions on Information Systems，2005，23(1): 3-34.

［7］ Mishra K N，Aaggarwal D A，Abdelhadi D E，et al.An efficient horizontal and vertical method for online DNA sequence compression［J］.International Journal of Computer Applications，2010，3(1):39-46.

［8］ Kaipa K K，Lee K，Ahn T，et al.System for random access DNA sequence compression［C］∥Proceedings of 2010 IEEE International Conference on Bioinformatics and Biomedicine Workshops.Hong Kong:IEEE，2010:853-854.

［9］ Mridula T V，Samuel P.Lossless segment based DNA compression［C］∥Proceedings of 2011 3rd International Conference on Electronics Computer Technology.Kanyakumari:IEEE，2011:298-302.

［10］ 纪震，周家锐，朱泽轩，等.基于生物信息学特征的DNA序列数据压缩算法［J］.电子学报，2011，39 (5):991-995. Ji Zhen，Zhou Jia-rui，Zhu Ze-xuan，et al.Bioimformatics features based DNA sequence data compression algorithm［J］.Acta Electronica Sinica，2011，39(5):991-995.

［11］ Ouyang J，Feng P，Kang J.Fast compression of huge DNA sequence data［C］∥Proceedings of 2012 5th IEEE International Conference on Biomedical Engineering and Informatics.Chongqing:IEEE，2012:885-888.

［12］ Allison L，Edgoose T，Dix T I.Compression of strings with approximate repeats［C］∥Proceedings of the 6th International Conference on Intelligent Systems for Molecular Biology.Montréal:AAAI，1998:8-16.

［13］ Loewenstern D，Yianilos P N.Significantly lower entropy estimates for natural DNA sequences［J］.Journal of Computational Biology，1999，6(1):125-142.

［14］ Korodi G，Tabus I.Normalized maximum likelihood model of order-1 for the compression of DNA sequences［C］∥Proceedings of 2007 Data Compression Conference. Snowbird:IEEE，2007:33-42.

［15］ Cao M D，Dix T I，Allison L，et al.A simple statistical algorithm for biological sequence compression［C］∥Proceedings of 2007 Data Compression Conference. Snowbird:IEEE，2007:43-52.

［16］ Pinho A J，Neves A J R，Ferreira P J S G.Inverted-repeatsaware finite-context models for DNA coding［C］∥Proceedings of the 16th European Signal Processing Conference.Lausanne:Technical Program Committee，2008.

［17］ Pinho A J，Neves A J R，Bastos C A C，et al.DNA coding using finite-context models and arithmetic coding［C］∥Proceedings of 2009 IEEE International Conference on Acoustics，Speech and Signal Processing.Taipei:IEEE，2009:1693-1696.

［18］ Pinho A J，Pratas D，Ferreira P J S G.Bacteria DNA sequence compression using a mixture of finite-context models［C］∥Proceedings of 2011 IEEE Statistical Signal Processing Workshop(SSP).Aveiro:IEEE，2011: 125-128.

［19］ Wang C，Zhang D.A novel compression tool for efficient storage of genome resequencing data［J］.Nucleic Acids Research，2011，39(7):e45/1-6.

［20］ Pinho A J，Pratas D，Garcia S P.GReEn:A tool for efficient compression of genome resequencing data［J］.Nucleic Acids Research，2012，40(4):e27/1-8.