一种基于改进FCM的自动图像分割算法*

周晓明 李钊 刘雄英

(1.华南理工大学理学院，广东广州510640;2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

模糊C均值聚类(FCM)是由Dunn［1］率先提出的，Bezdek［2-3］对该理论进行了完善，他不仅证明了该算法的收敛性，而且给出了该算法基于最小二乘迭代的优化算法.

FCM算法因迭代简单，且其模糊性符合人眼的视觉习惯，因而在图像分割领域得到了广泛的应用［4］.传统的FCM分割方法是将像素的灰度值作为聚类特征进行聚类以得到各个像素的类属，属于同一类属的像素归为同一个区域以完成图像分割，但是直接运用FCM算法进行图像分割需要人为确定聚类数，而人为确定聚类数往往存在许多不足:①主观性较强，不同人对同一幅图像往往得到不同的聚类数目;②由于人眼受图像相邻区域对比度的影响，往往只能确定图像的区域数，而区域数不等于聚类数，因为不同的区域若其灰度值相近则在聚类过程中应该属于同一类;③降低了FCM算法的自动化程度.基于以上原因解决聚类数需人为确定的问题具有十分重要的意义.

如何确定数据集的聚类数是所有聚类算法面临的一个关键问题，也是聚类有效性的一个重要的研究方向.传统的解决方法是先定义一个聚类有效性指标V，该指标是关于聚类数c的函数.然后对不同的c值计算其相应的V值.对于某一数据集，若V是关于c的单调函数，则函数曲线的拐点处对应的c值被认为是最佳聚类数，若V不是关于c的单调函数，则函数在最值处对应的c值被认为是最佳聚类数.近十几年来，有多种聚类有效性指标被学者相继提出［5-18］.这里先作简单的介绍.

Xie等［6］定义第j类的类内紧凑度为Comp(j)，再用相距最近的两个聚类中心的距离度量类间的分散度Sep(c)，则有效性指标被定义为Comp(j)之和与Sep(c)的商.Campello等［11］提出了另一种指标VF_sil.设d(i，j)是样本i到类j的距离.首先将各个对象依据最大隶属度原则进行聚类，然后对每一个样本i，设其属于第j类，则可计算出si，si=1-然后对每个s加权i求和得到VF_sil.

Bouguessa等［10］用类内模糊协方差矩阵的迹度量聚类紧凑度，用类间模糊协方差矩阵的迹度量类间的分离度.令类内模糊协方差矩阵为Fj，类间模糊协方差矩阵为SB，则有效性指标VSCG为SB的迹与Fj的迹之和的商.

这类确定聚类数的方法虽然直观清晰，但存在一些明显的不足:首先每种有效性指标往往只适合特定分布的数据集，对同一数据集，不同的有效性指标往往得到不同的最佳聚类数，因此Pal等［13］指出，运用一个有效性指标确定数据集的聚类数往往是不可信的;其次采用这种试探性的方法将大大增加算法的计算量，从而限制了其在实际中的应用.

文中提出的算法避免了采用聚类有效性指标来自动确定聚类数目，而是根据图像这类数据集的特点对其进行4叉树结构的子图分解，直到子图满足一定条件时进行聚类数为2的FCM聚类分割，最后依据一定条件进行区域合并从而避免了聚类数的直接确定.此外，由于FCM的迭代运算是一种高次运算，对子图进行聚类相当于将一个数据集分成若干部分单独聚类，降低了每次参与聚类的对象数目，因而相对于对整张图像进行聚类降低了计算量.

1 FCM背景理论

FCM算法通过最小化目标函数来实现样本的最优划分.假设将n个样本聚成c类，则目标函数为且满足约束条件i=1，2…，n，μij＞0.其中，xi为样本i的特征向量，vj是第j类的聚类中心，μij为样本i关于j类的隶属度，m为权重函数，文献［13］从聚类有效性的实验中得到m的取值为1.5～2.5，本研究取m=2. FCM算法通过更新vj和μij来优化目标函数.根据拉格朗日条件极值理论可得到更新公式:

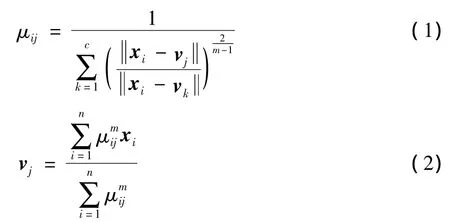
当相邻的两轮迭代得到的目标函数值满足: |Jt-Jt+1|＜ε，则可以认为已经得到较好的聚类结果从而停止更新，其中ε是一个很小的正数，称为容许误差.最后根据隶属度最大原则将样本划分到其隶属度最大值对应的类中.

2 基于子图分解与区域合并的FCM自动分割算法

2.1 图像直方图的信息熵与聚类峰值数

图像直方图是图像的一种十分重要的统计信息，它很好地反映了图像的灰度分布情况，其波峰和波谷是直方图非常有用的信息，文中定义两个参数来描述图像的直方图.

(1)直方图的信息熵

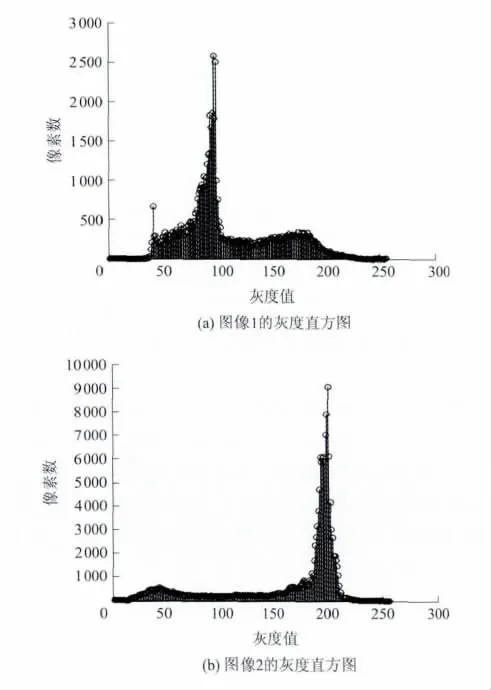
图1 信息熵的比较Fig.1 Contrast of the information entropy

(2)直方图的波峰数估计

直方图的不规则性会产生大量假的波峰和波谷，因而其波峰数难以统计，为解决这一问题，对图像归一化处理后的直方图进行FCM聚类处理.以聚类后的直方图的波峰数估计原直方图的波峰数，具体步骤如下:

①计算图像的64级灰度直方图，得到数组h，h包含64个元素，每个元素的取值为图像取该级灰度的像素数.

③对t的64个元素进行聚类数为2的FCM聚类，初始聚类中心为{0}和{1}，容许误差取0.001.

④按隶属度最大原则对元素进行归类，得到聚类直方图s.计算s的波峰数peak_n作为h波峰数的估计值.

聚类后的直方图没有了原始直方图的许多细小波动，而这些细小波动往往会被误认为波峰或波谷.图2所示为原始直方图与聚类后的直方图，聚类后的直方图显示峰值数为2.

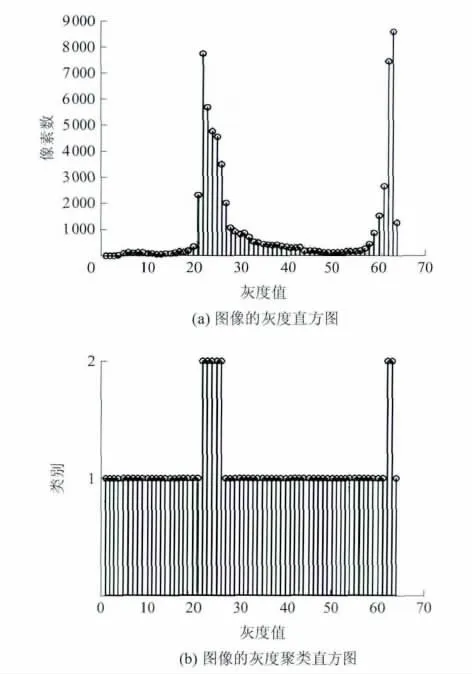
图2 原始直方图与聚类后的直方图Fig.2 Original histogram and the histogram after clustering

2.2 区域间的巴氏距离

巴氏距离是衡量直方图相似性的常用标准，巴氏距离越大，则两个直方图越相似.文中通过计算图像两个相邻区域直方图的巴氏距离来衡量这两个区域的相似度.

2.3 整体算法流程

1)基于子图分解的FCM图像分割

进行图像分割时先将图像划分为子图直到子图满足以下两点中的一点:

(1)子图直方图的inf小于原图直方图的inf且子图直方图的peak_n小于等于2;

(2)子图大小小于一定阈值α，α可以根据图像中最小区域的面积进行调整，文中统一取1024.

此时对子图的像素做聚类数目为2的FCM聚类.聚类后根据最大隶属度原则对像素进行分类.进行聚类分割时初始聚类中心均设为{0，255}，容许误差取0.001.

2)基于区域面积与巴氏距离的区域合并

林木资源资产个体的生长发育及投入产出情况具有阶段性，不同类型林木资产每个阶段具有不同的生长发育特性，只有充分掌握各自特点才能便于后期经济价值的核算以及体系的建立。

基于原始图像子图的分割将会使得分割得到的区域数大于实际的区域数，因此进行适当的区域合并是必要的.文中的区域合并基于以下两条准则:

(1)若两个相邻区域的巴氏距离ρ(r，q)大于阈值β，则将他们合并.文中β统一取0.22.

(2)若区域的面积小于阈值γ，则将其合并到灰度值均值与其最接近的相邻区域中.γ也是与图像的最小区域的面积有关，文中统一取50.

为了更清晰地叙述本文算法流程，这里将算法的流程用流程框图表示出来，如图3所示.

3 实验结果分析

以rice图为例展示文中算法的具体过程及中间结果.图4(a)为待分割的rice图，图4(b)是基于子图分解的FCM聚类分割后的结果，图4(c)是基于相邻区域巴氏距离进行区域合并后的结果，图4(d)是合并掉小区域后的结果.

文中提出的算法将与传统人为确定聚类数的方法和两种较经典的自动确定聚类数的指标(F_stl有效性准则［11］和SCG有效性准则［10］)相比较，采用有效性准则时将分别计算聚类数为2～10的情况下这两个准则的取值，取最大值对应的聚类数作为最佳聚类数.聚类时容许误差统一取0.001.

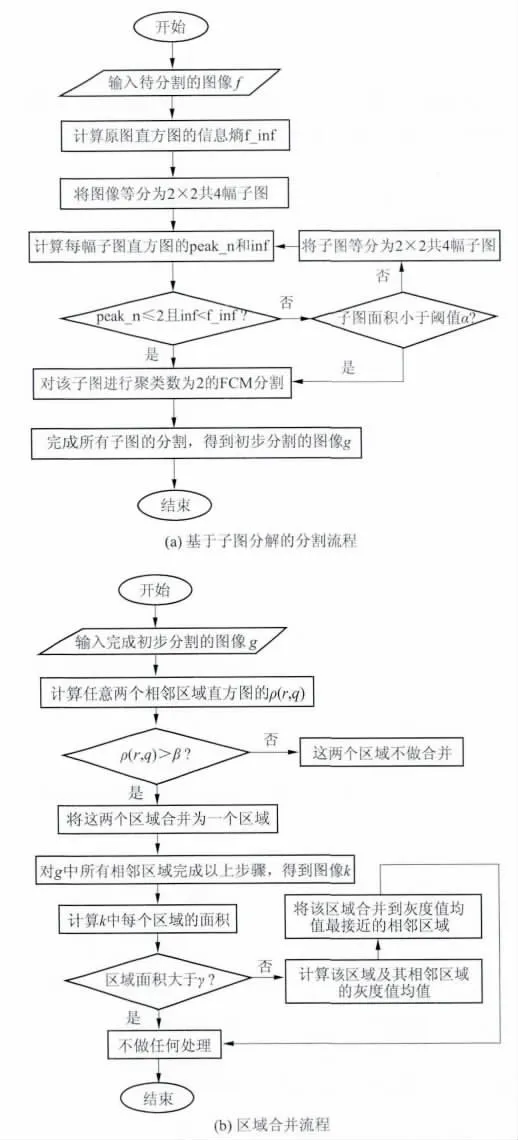
图3 提出的算法流程图Fig.3 Proposed algorithm flowchart

表1示出了F_stl有效性准则和SCG有效性准则对于3幅图像在不同聚类数下的取值.表2示出了人工方法及这两个准则对于这3幅图像得到的聚类数.从结果可以看出，F_stl准则和人工方法在确定最佳聚类数时具有较一致的结果，SCG准则容易受光照不均匀等因素的影响，所产生的最佳聚类数与前两种方法有较大差距.

图4 rice图的分割过程Fig.4 Segmentation process of rice image

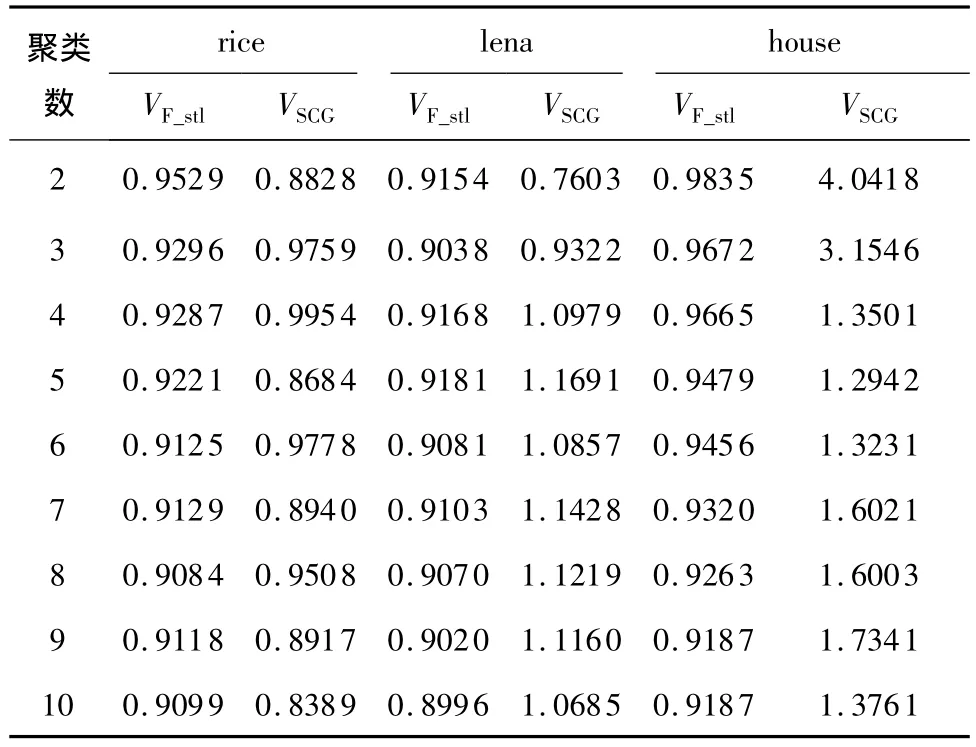
表1 实验图像的有效性指标Table 1 Validity index of experiment images

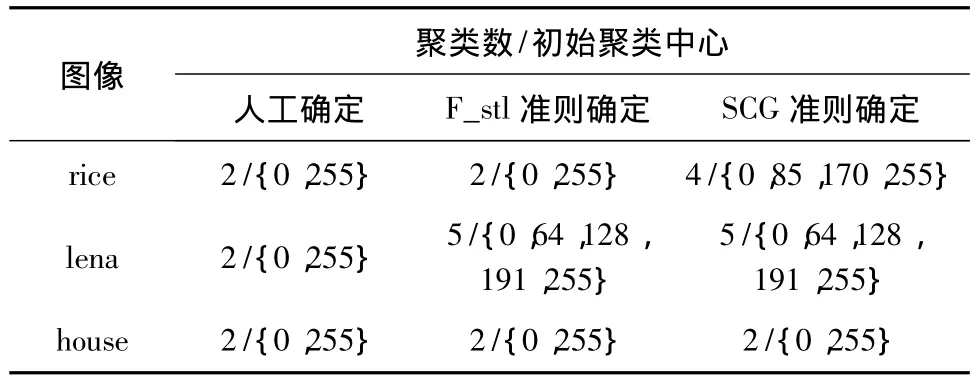
表2 图像的最优聚类数Table 2 Optimal clustering number of images

图5 rice图实验结果Fig.5 Experiment results of rice image

图6 lena图实验结果Fig.6 Experiment results of lena image

图5(a)在聚类数为2的情况下可以得到较好的分割效果，但由于光照不均匀的影响在图片下方的米粒出现了不同程度的缺损.相比之下文中算法可以很好地将所有米粒完整分割出来，且整个过程无需人工干预.

图6(a)在聚类数为2的情况下得到的分割效果要优于聚类数为5的情况，但由于部分区域内的灰度值波动较大，因而在人物脸部出现一些错误分割.而文中算法可以将脸和肩的轮廓分割出来.

图7(a)在聚类数为2的情况下可以得到不错的聚类效果，但在左边十字架等区域出现了区域不完整的现象.相较而言，文中算法分割出来的区域比较连续完整.

图7 house图实验结果Fig.7 Experiment results of house image

此外文中算法由于不需直接确定聚类数，因此避免了对最佳聚类数的搜索，而且由于FCM的迭代运算是一种高次运算，对子图进行聚类相当于将一个数据集分成若干部分单独聚类，降低了每次参与聚类的对象数目，在聚类对象总数一定的情况下这种分治的方法有助于降低运算量.

表3示出了不同算法分割这3幅图片的耗时，仿真实验运行的硬件环境为AMD Athlon(tm)64 X2 Dual Core Processor 4400++，CPU主频为2.30GHz，内存为2.00GB.编程环境为Matlab7.0.从表3的运行时间对比可以看出，采用基于聚类有效性指标的方法进行聚类数的自动确定是十分耗时的.而文中提出的算法在实现自动分割的基础上避免了聚类数目的直接确定，同时基于子图的FCM分割减少了每次聚类的对象集规模，因而大幅降低了运算量.

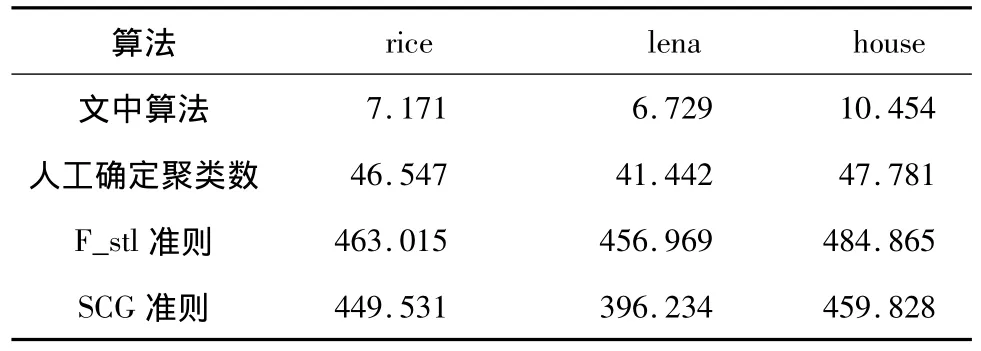
表3 4种方法的运行时间对比Table 3 Contrast of operating time of four methods s

为了对分割结果进行一定的定量分析，文中对rice图进行了人工分割并将以上算法的分割结果与之对比，定义了3个指标来描述分割算法的准确度.设算法分割图中划分为米粒且实际属于米粒的像素数为n1，算法分割图中划分为米粒的总像素数为m1，算法分割图中划分为背景且实际属于背景的像素数为n2，算法分割图中划分为背景的总的像素数则有以下定义:对象分割正确率;背景正确分割率;总体分割正确率

表4示出了文中算法和各项对比算法的指标计算结果.从表中可以看出文中算法的分割结果和人工的分割结果十分接近，人工确定聚类数下的分割可以得到较高的对象分割正确率，但由于光照不均匀的影响使得图片下方的米粒出现残缺从而降低了背景分割正确率.而SCG准则下的分割结果正确率最低.

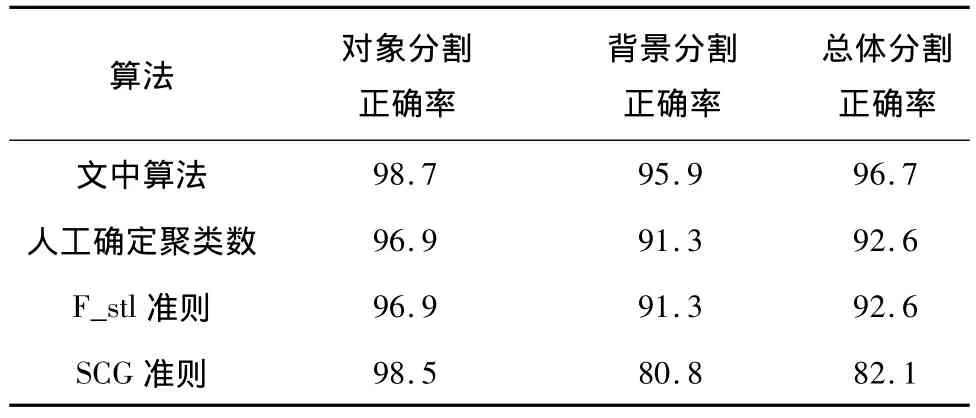
表4 4种方法的正确率对比Table 4 Contrast of correct rates of four methods %

4 结语

针对FCM用于图像分割时聚类数难以自动确定这一问题，传统的基于聚类有效性分析的自动聚类数确定方法存在着准确度低与运算量大等缺点.文中提出一种新的算法用于解决该问题.该算法对先对图像进行4叉树结构的子图分解，然后通过分析子图直方图的信息并结合子图的大小决定继续分解还是进行聚类数固定的FCM分割，最后分析相邻区域的相似度并结合区域的面积进行区域合并.在3幅实际图像上的实验表明，该算法可以避免聚类数的直接确定，具有较好的分割效果且大幅降低了运算量.

［1］ Dunn J C.A fuzzy relative of the ISO DATA process and its use in detecting compact well-separated clusters［J］. Journal of Cybernetics，1974，3(3):32-57.

［2］ Bezdek J C.Pattern recognition with fuzzy objective function algorithms［M］.New York:Plenum Press，1981:20-35.

［3］ Bezdek J C.A convergence theorem for the fuzzy iso data clustering algorithms［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1980，PAMI-2(1):1-8.

［4］ Kettaf F Z，BI D，Asselin de Beauville J P.A comparison study of image segmentation by clustering techniques［C］∥Proceedings of 3rd International Conference on Signal Processing.Beijing:Chinese Institute of Electronics，1996: 1280-1290.

［5］ Chen M Y，Linkens D A.Rule-base self-generation and simplification for data-driven fuzzy models［J］.Fuzzy Sets and Systems，2004，142(2):243-265.

［6］ Xie X L，Beni G.A validity measure for fuzzy clustering［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13(8):841-847.

［7］ Xie Y，Raghavan V V，Dhatric P，et al.A new fuzzy clustering algorithm for optimally finding granular prototypes［J］.Approximate Reasoning，2005，40(1):109-124.

［8］ Gath I，Geva A B.Unsupervised optimal fuzzy clustering［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):773-781.

［9］ Tsekouras G E，Sarimveis H.A new approach for measuring the validity of the fuzzy c-means algorithm［J］.Advances in Engineering Software，2004，35(8/9):597-875.

［10］ Bouguessa M，Wang S R.A new efficient validity index for fuzzy clustering［C］∥Proceedings of the Third International Conference on Machine Learning and Cybernetics.Shanghai:The Hong Kong Polytechnic University，2004:26-29.

［11］ Campello R J G B，Hruschka E R.A fuzzy extension of the silhouette width criterion for cluster analysis［J］. Fuzzy Sets and Systems，2006，157(21):2858-2875.

［12］ Cho S B，Yoo S H.Fuzzy Bayesian validation for cluster analysis of yeast cell-cycle data［J］.Pattern Recognition，2006，39(12):2405-2414.

［13］ Pal N R，Bezdek J C.On cluster validity for fuzzy cmeans model［J］.IEEE Transactions on Fuzzy Systems，1995，3(3):370-379.

［14］ 贲圣兰，苏光大.基于错误度量的模糊聚类有效性函数［J］.模式识别与人工智能，2010，23(1):11-16. Ben Sheng-lan，Su Guang-da.A fuzzy cluster validity index based on clustering mistake measures［J］.Pattern Recognition and Artificial Intelligence，2010，23(1): 11-16.

［15］ 周世兵，徐振源，唐旭清.基于近邻传播算法的最佳聚类数确定方法比较研究［J］.计算机科学，2011，38(2):225-228. Zhou Shi-bing，Xu Zhen-yuan，Tang Xu-qing.Comparative study on method for determining optimal number of clusters based on affinity propagation clustering［J］. Computer Science，2011，38(2):225-228.

［16］ 张爱华.基于模糊聚类分析的图像分割技术研究［D］.武汉:华中科技大学计算机科学与技术学院，2004.

［17］ 周世兵，徐振源，唐旭清.一种基于近邻传播算法的最佳聚类数确定方法［J］.控制与决策，2011，26 (8):1147-1152. Zhou Shi-bing，Xu Zhen-yuan，Tang Xu-qing.Method for determining optimal number of clusters based on affinity propagation clustering［J］.Control and Decision，2011，26(8):1147-1152.

［18］ 杨锐.基于模糊聚类及水平集方法的图像分割技术研究［D］.长春:吉林大学电子科学与工程学院，2011.