磁共振用Halbach永磁阵列的仿真分析*

张广才 刘朝阳 陈巧燕，3 陈方 杨晓冬†

(1.中国科学院苏州生物医学工程技术研究所，江苏苏州215163;2.中国科学院武汉物理与数学研究所，湖北武汉430071;3.中国科学院大学，北京100049)

核磁共振技术已经在生物、物理、化学、医学等领域得到广泛的应用，其更是成为临床诊断必不可少的手段之一.大型的超导高场磁共振仪器是当今磁共振技术发展的一个热点，但是小型化、便携式的永磁低场核磁共振设备更适用于工业和食品检测、探矿、考古、大分子结构分析等方面［1-4］.

小型核磁共振仪器多采用传统永磁体，这类磁体由于铁轭的存在，体积大，比较笨重，且可利用空间有限，漏磁严重，磁场强度有限.因此，需要设计一种无铁轭，且磁场可利用空间大的磁体类型.20世纪80年代，美国物理学家K.Halbach设计了一种新型无铁轭多级磁体结构，被称为Halbach阵列［5］.这种永磁体结构是由多个磁块按照一定的规律组合成的，相邻的磁块具有不同的充磁方向，且能产生较理想的单边磁场.由于它的优异特性，得到了学者和工程人员的广泛关注，并且被应用于诸多领域.根据组合后的磁体形状一般分为直线型和圆柱型Halbach阵列两大类.直线型Halbach阵列是一种最基本的组合方式，主要用于制造直线电机［6］，可用于磁悬浮列车.圆柱型 Halbach阵列可以看做将直线型Halbach阵列首尾相接组成的，其又可分为多对极的和单对极的圆柱型Halbach阵列两种.多对极圆柱型Halbach阵列主要用于永磁电机和永磁轴承等领域.而单对极圆柱型Halbach阵列由于其不带铁磁材料、漏磁小和高均匀性的特性曾被丁肇中等用于阿尔法磁谱仪中［7］;此外，随着磁共振仪器小型化和便携化的发展需求，单对极圆柱型Halbach阵列逐渐应用于核磁共振检测和成像等方面［8-15］.单对极圆柱型Halbach阵列是文中主要研究对象，下文提及的 Halbach阵列皆是对它的特指.德国的B.Blümich课题组对Halbach阵列进行了深入研究，在2004年提出了一种由相同的16个方形磁块组成的Halbach阵列，将其用于岩心的磁共振分析［9］; 2007年提出了一种轴向多层磁块组成阵列的改进，这样减小了端部的磁场衰减［10］;2010年他们又提出了一种尺寸更小，场强达到0.7 T且形状可调的Halbach阵列［12］;2011年该课题组更是设计了一种可用于植物茎、非金属管等检测的可开口式Halbach阵列［13］.瑞士的Moresi等［8］也提出一种由8块圆柱形磁块组成的Halbach阵列，该设计降低了制造成本和工装难度.Hills等［11］设计了一种由4块磁块组成的开放式Halbach阵列，这方便使用多个传感器对同一个样品检测.国内对于Halbach阵列在核磁共振上的应用研究也取得了一定成果.乔德治［15］先后设计了一种等腰三角形和新月形的Halbach阵列，这两种形式磁块间的磁场力比扇形的磁场力小，更便于安装.

文中介绍了Halbach阵列的原理及其磁场特点;然后对用于核磁共振成像的、小型的、圆柱型的单对极Halbach阵列进行Maxwell仿真，重点分析了离散磁块数目、尺寸、材料对Halbach阵列磁场的影响，并与现有文献仿真结果进行了对比;此外还分析了非理想情况下磁场的误差;最后与传统H型永磁体进行了对比，验证了Halbach阵列的优越性.

1 Halbach阵列原理

理想的Halbach阵列的磁化方向在圆周上是连续变化的，且磁体是无限长的，因此其可被视为二维磁场.而其内腔所产生的磁场方向可根据稀土永磁材料的易轴旋转理论得知，即当二维空间中不存在导磁材料时，若全部的永磁体的磁化方向角度变化θ，那么在此空间中的所有的磁场方向的角度变化为-θ，且幅值不变.这说明Halbach阵列在内腔产生的磁场是同一方向且幅值相等的均匀场.那么理想状态下，当磁体的磁极对数N=1时的Halbach阵列，其磁化方向角度θ与极坐标角度φ的关系为

若设其内半径为ri、外半径为ro、剩磁为Br，那么其圆柱内腔的均匀磁场的磁感应强度Bp为

由上式可知，Halbach阵列的磁感强度主要和圆柱的内外径的比值和永磁材料的磁性能有关.

但是在Halbach阵列的实际制造过程中，由于永磁材料的制备和磁体充磁技术的限制，无法实现理想状态.因此，采用离散磁块组合实现Halbach阵列.对于单对极圆柱型Halbach阵列来讲，若将其分为M块相同扇形磁块的话，那么每个磁块的夹角为

由于无法实现磁化方向连续，因此要保证每个磁块不具有一致的磁化方向，而其相邻的下一个磁块的充磁方向需改变的角度为

图1给出一个M=6的Halbach阵列的示意图，从图中可知，其单个扇形磁块的夹角为60°，相邻两个磁块间充磁方向的夹角为120°.

这种通过离散的单个磁块组合得到Halbach阵列的方式必然引入一定程度的误差，使得实际得到的Halbach阵列的磁感强度和磁场的均匀性与理想值有一定的误差.不过，可以通过增加离散的磁块数M来接近理想值，但是M的增大必然会使加工成本和工装难度增大，这也是实际应用中必须要考虑的，可以在适当情况下选择折中的设计.

图1 M=6时的Halbach阵列Fig.1 Halbach array when M=6

2 Halbach阵列仿真分析与对比

对于永磁体产生的静磁场的磁场分布研究，通常使用电磁场理论进行分析计算.常用的电磁场分布的数值计算方法有积分方程法、有限差分法、有限元法和边界元法等［16］.但是实际应用中，常用一些有限元分析的商用软件，如ANSYS、Magnet、Maxwell等.

文中使用Ansoft公司的Maxwell仿真分析软件对Halbach阵列进行仿真分析，下面分别对理想状态下不同参数的Halbach阵列进行了对比，并且对存在充磁误差、磁块之间性能误差或者二者都有的非理想情况与理想情况下的Halbach阵列的静磁场进行了对比，最后给出了常规永磁体与Halbach阵列的对比.

2.1 理想情况下的Halbach阵列仿真

(1)8子块和16子块的Halbach阵列模型与仿真文中设计了一种内半径ri=21mm、外半径ro= 30mm、高度H=50mm的Halbach阵列.图2和图3分别示出了8子块和16子块Halbach阵列的2D模型、3D模型、充磁方向和其产生的磁场方向.由式(3)和式(4)可知，8子块Halbach阵列的单块夹角为45°，相邻两块之间的充磁方向夹角为90°;而16子块Halbach阵列的单块夹角为22.5°，相邻两块之间的充磁方向夹角为45°.

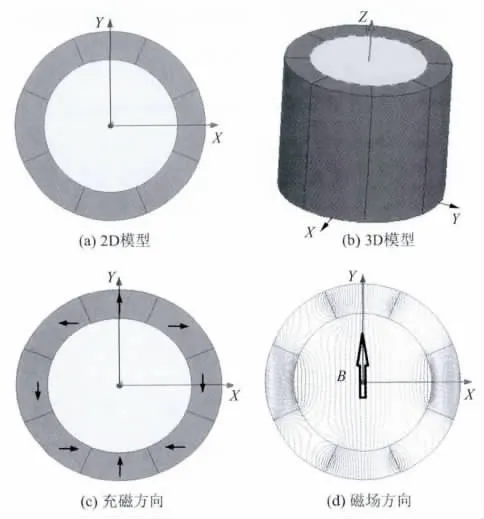
图2 8子块Halbach阵列Fig.2 Halbach array including 8 sub-blocks

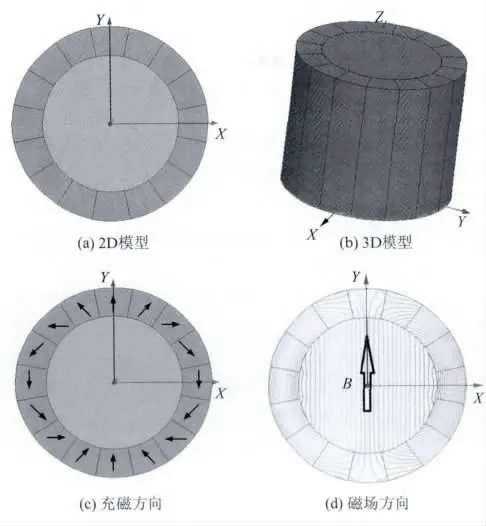
图3 16子块Halbach阵列Fig.3 Halbach array including 16 sub-blocks

图4示出了相同尺寸的8子块和16子块Halbach阵列3D模型的仿真结果，其内腔的球域中半径r=10mm.从图中可以看出，在该球域内8子块Halbach阵列所产生的磁感强度B范围为0.37973～0.39518T，而16子块Halbach阵列产生的磁感强度范围为0.41587～0.41820 T，因此可知在尺寸相同的情况下，块数越多的Halbach阵列在相同位置产生的磁感强度越强.

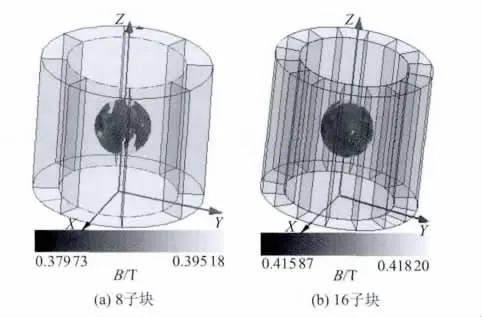
图4 不同块数、相同尺寸Halbach阵列的磁感强度Fig.4 Magnetic induction density of Halbach arrays with same size and different numbers of sub-blocks

(2)尺寸不同的16子块Halbach阵列仿真

图5分别示出了两个不同尺寸的16子块Halbach阵列2D仿真，其外半径分别为30和40mm，内半径均为21mm，内腔圆形区域半径r=10mm.从两图可以看出，在内径相同时，外径越大，其所能产生的磁感强度越强，即外径和内径的比值越大，磁感强度越大.

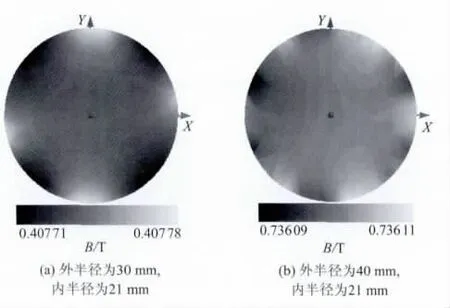
图5 不同尺寸Halbach阵列内腔r=10mm圆域的磁感强度分布Fig.5 Magnetic induction density distribution of the ball region (r=10mm)within the cavity of Halbach array

(3)材料不同的Halbach阵列仿真

表1示出了型号为Nd35的钕铁硼材料和型号为Sm24的钐钴材料的磁性能参数，从表中可以看出Nd35的磁性能相对Sm24的更好.图6示出了使用两种不同材料的16子块Halbach阵列3D仿真情况下在相同位置产生的磁感强度，从图中可以看出使用Nd35的Halbach阵列在半径r=5 mm的圆周上产生的磁感强度约为416 mT，而使用Sm24的在相同位置磁感强度约为345 mT.这说明其他条件相同情况下，材料的磁性能越好其产生的磁感强度相对越高.

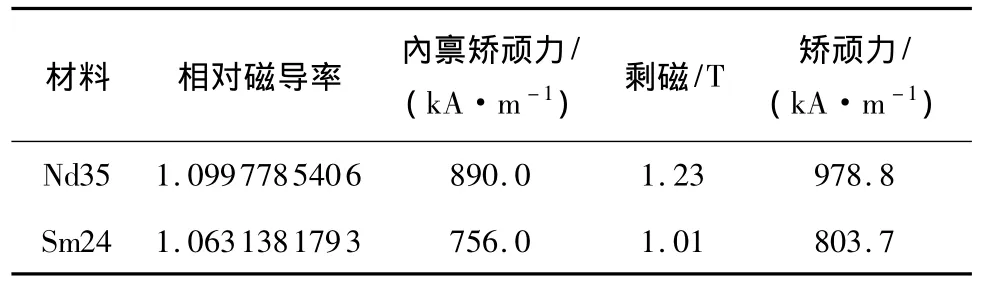
表1 两种材料的磁性能参数Table 1 Magnetic parameters of two types of material

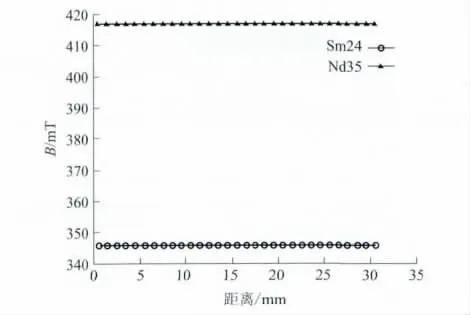
图6 材料不同的16子块Halbach阵列相同位置的磁感强度的分布对比Fig.6 Comparison of magnetic induction density distribution of Halbach arrays with 16 sub-blocks and at the same position same size but different materials

(4)与现有文献中仿真结果的对比

文献［15］中应用等效磁网络法对8子块的Halbach阵列进行了2D建模仿真，其尺寸为ri=25mm、ro=40 mm，仿真后内腔磁感强度为 0.350 00～0.55000T，文中应用Maxwell软件进行同样仿真得到结果为0.35214～0.54973T，仿真结果近似，可见文中方法是正确的.

2.2 非理想情况下的Halbach阵列仿真

2.2.1 充磁角度存在误差的情况

充磁是Halbach阵列加工的一个重要步骤，若磁块存在充磁角度误差，会导致磁场值发生变化.图7示出16子块Halbach的每个磁块编号标记，若其中编号为“3”、“6”、“11”和“16”的磁块误差值分别为-1°、+1.5°、-1°和+0.5°，实际充磁角度大于理想值表示为“+”，反之为“-”.图8示出了存在角度误差的非理想状况下Halbach阵列2D仿真区域内磁感强度的分布，其区域半径r=10 mm.通过和图5(a)的对比可以看出，存在角度误差时Halbach阵列在指定区域内产生的磁感强度范围更大，即其磁场均匀性更差.

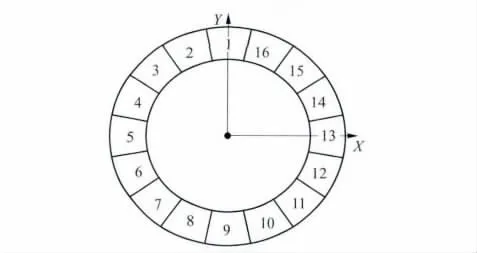
图7 磁块编号Fig.7 Number of magnetic blocks

图8 存在角度误差的Halbach阵列2D仿真Fig.8 2D simulation of Halbach array with the errors of magnetizing angles

2.2.2 磁块的磁性能存在差异的情况

相同牌号的磁材也存在性能差异，这也会引起实际磁场值的变化.若图7中编号为“3”和“11”的磁块的3个磁性能参数都降低了5%，而编号为“6”和“16”的磁块相应的降低了10%，那么Halbach阵列2D仿真的r=10mm的内腔区域的磁感强度分布如图9所示.对比图5(a)和图9可以看出，存在磁性能误差时Halbach阵列在指定区域内产生的磁感强度范围更大，因此其磁场均匀性更差.

2.2.3 存在充磁角度误差和磁块性能差异的情况

当Halbach阵列中编号为“3”、“6”、“11”和“16”的磁块同时出现上述的充磁角度误差和磁性能差异时，Halbach阵列2D仿真的r=10mm的内腔区域的磁感强度分布如图10所示.通过图10与图8、图9的对比可以看出，当两种误差都存在时Halbach阵列在指定区域产生的磁场的均匀性比单一存在一种误差时的均匀性还要差.

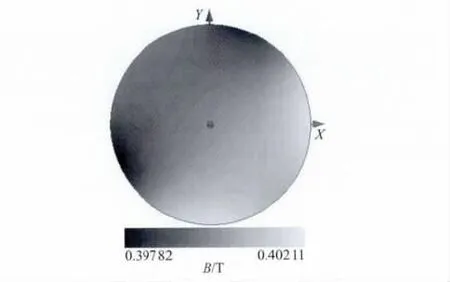
图9 存在磁性能差异的Halbach阵列2D仿真Fig.9 2D simulation of Halbach array with the difference of magnetic properties

图10 存在角度误差和磁性能差异的Halbach阵列2D仿真Fig.10 2D simulation of Halbach array with the errors of magnetizing angles and the difference of magnetic properties

2.3 与H型永磁体的对比

为体现 Halbach阵列的优越性，设计了一种H型常规永磁体结构，其工作空隙与图3的16子块Halbach阵列的内腔尺寸相同，都为42 mm，磁块尺寸为Φ150mm×24mm，匀场极板的尺寸为Φ150mm× 20 mm，而磁体外形尺寸则为300 mm×180 mm× 200mm，如图11所示.图12示出了该磁体在工作空隙中心处r=10 mm的球域内B值分布.通过图11和图3中两种永磁体的尺寸，可分别计算出H型永磁体和Halbach永磁体的磁材用量和磁体体积，分别是847.8、10800.0 cm3和495.9、2826.0 cm3;通过图4(b)和图12的对比可知，在r=10mm的内腔球域内，Halbach阵列比H型永磁体的磁感强度高.由此可知，在相同尺寸工作空隙的情况下Halbach阵列磁体相对于传统H型永磁体具有体积小、重量轻，产生的磁场强度较高等优点.这是由于Halbach阵列磁体结构具有增强腔内磁场、漏磁小的特性决定的.

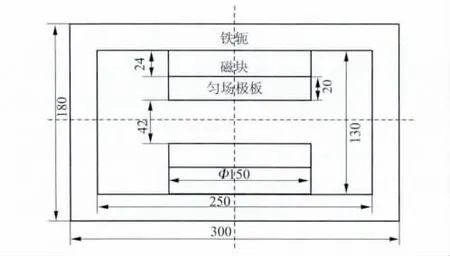
图11 H型永磁体的结构图(单位:mm)Fig.11 Structure diagram of H-style permanent magnet(Unit:mm)

图12 H型永磁体工作空隙内r=10 mm的球域的磁感强度分布Fig.12 Magnetic induction density distribution of the ball field(r=10 mm)within the work gap of H-style permanent magnet

3 结论

文中使用Maxwell软件对Halbach阵列进行仿真分析，通过对不同参数的Halbach阵列的对比发现，Halbach阵列所产的磁感应强度与磁性材料的性能、阵列的外、内径尺寸的比值以及阵列组成的块数成正比，这些结果可为Halbach阵列的设计和优化设计提供指导;还对存在充磁角度误差和磁块性能差异等非理想情况下的Halbach阵列进行了仿真，发现磁块选材、充磁等磁体加工工艺对Halbach阵列磁场的均匀性有重要影响.此外，还发现Halbach阵列相对常规磁体在用料和磁场强度方面更有优势.但是Halbach阵列的加工工艺比较复杂，影响了它的推广和使用，今后仍需在该方面进行深入研究.

［1］ Marko A，Wolter B，Arnold W.Application of a portable nuclear magnetic resonance surface probe to porous media［J］.Journal of Magnetic Resonance，2007，185(1):19-27.

［2］ Chang Wei-Hao，Chen Jyh-Horng，Hwang Lian-pin.Single-sided mobile NMR apparatus using the transverse flux of a single permanent magnet［J］.Magnetic Resonance Imaging，2010，28(1):129-138.

［3］ Gädke A，Dykstra R.Mobile permanent magnet NMR systems for field studies on Antarctic Sea ice［C］∥Proceedings of the 10th Colloquium on Mobile Magnetic Resonance(CMMR10).Leipzig:AIP，2010，1330:113-116.

［4］ Lee H，Sun E，Ham D，et al.Chip-NMR biosensor for detection and molecular analysis of cells［J］.Nature Medicine，2008，14(8):869-874.

［5］ Halbach K.Design of permanent multipole magnets with oriented rare earth cobalt materials［J］.Nuclear Instruments and Methods，1980，169(1):1-10.

［6］ Lei M Z，Dai W Z，Wang L Q.Analysis on a novel Halbach-type transverse-flux linear oscillatory motor for linear compressor［J］.Applied Mechanics and Materials，2013，241-244(9):1431-1437.

［7］ 夏平畴.用于α磁谱仪的永磁磁体的设计问题［J］.现代科学仪器，1998(3):3-4. Xia Ping-chou.Design of permanent magnet for alpha magnetic spectrometer［J］.Modern Scientific Instruments，1998(3):3-4.

［8］ Moresi G，Magin R.Miniature permanent magnet for tabletop NMR［J］.Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering，2003，19B(1):L35-43.

［9］ Anferova S，Anferov V，Rata D G，et al.A mobile NMR device for measurements of porosity and pore size distributions of drilled core samples［J］.Concepts in Magnetic Resonance Part B:Magnetic Resonance Engineering，2004，23B(1):26-32.

［10］ Anferova s，Anferov V，Arnold J，et al.Improved Halbach sensor for NMR scanning of drill cores［J］.Magnetic Resonance Imaging，2007，25(4):474-480.

［11］ Hills B，Wright K，Gillies D.A low-field，low cost Halbach magnet array for open-access NMR［J］.Journal of Magnetic Resonance，2005，175(2):336-339.

［12］ Danieli E，Perlo J，Blüemich B，et al.Small magnets for portable NMR spectrometers［J］.Angewandte Chemie International Edition，2010，49(24):4133-4135.

［13］ Windt C，Soltner H，van Dusschoten D，et al.A portable Halbach magnet that can be opened and closed without force:the NMR-CUFF［J］.Journal of Magnetic Resonance，2011，208(1):27-33.

［14］ Linck Y，Killner M，Danieli E，et al.Mobile low-field 1H NMR spectroscopy desktop analysis of biodiesel production［J］.Applied Magnetic Resonance，2013，44(1/2): 41-53.

［15］ 乔德治.基于等效磁网络改进Halbach阵列的研究［D］.北京:北京工业大学交通学院，2010.

［16］ 武海登.MRI磁体系统的计算机辅助设计研究［D］.合肥:中国科学技术大学信息科院技术学院，2007.