直行优先情况下左转车冲突延误模型研究

郑长江，徐 瀚，陈田星

(1.河海大学 土木与交通学院，江苏 南京 210098；2.江苏省交通科学研究院，江苏 南京 210017)

我国交通规则规定，通行信号灯启亮后，直行交通流优先通行，左转交通流以相互穿越的方式通过冲突点，用于直行优先信号控制交叉口的延误计算模型，较为公认的有英国TRRL的韦伯斯特(F.V.Webster)模型、美国的HCM模型等，但是这些模型仅能计算停车线前的延误，无法分析计算同一相位内有冲突交通流的第2次延误。

冯军红,等[1]在研究改进的HCM延误模型基础上，考虑了左转车流驶离交叉口时非机动车驶入机动车道从而造成左转车流的跟驰延误，建立了一个两相位信号交叉口左转交通流延误模型；宋现敏,等[2]在借鉴无信号控制交叉口次路车流Admas延误模型的基础上，推导了信号交叉口左转车流的冲突延误计算模型，然后应用概率论、间隙理论及排队论的相关知识建立了直行车的冲突延误计算模型；赖元文,等[3]分析了车辆到达和离去规律，采用排队增量累计(IQA)方法，提出基于IQA方法的信号交叉口计算左转延误计算模型，通过使用不规则的多边形来计算队列累积面积作为均匀延误值；李丽丽[4]根据排队论和可插车间隙理论建立了左转车流与直行车流在冲突点处的延误模型；杨晓光[5-6]假设直行车车头时距服从负指数分布推导了左转车在冲突点处经历的延误；马国胜,等[7]采用M3分布来描述交叉口车头时距分布，并考虑左转车排队延误以及1个周期内绿初直行车排队数对冲突延误的影响，建立两相位交叉口冲突延误改进模型。

笔者推导假设直行车车头时距服从M3分布，利用概率论、排队论的相关理论知识，推导两相位交叉口直行优先情况下左转车在冲突点处的延误模型。

1 基本假定

1)交叉口为典型十字交叉口，车道功能划分为：1条左转专用车道、1条直行专用车道、1条右转专用车道，如图1。

2)本向左转车与对向直行车在一个相位内存在冲突。

3)左转交通流利用对向直行交通流的可穿越空挡，或绿灯末期的时间通过交叉口。

4)左转车车头时距服从负指数分布、对向直行车车头时距服从M3分布。

5)交叉口交通流饱和度<1。

6)所有驾驶员具有相同的特性，也就是所有驾驶员的临界间隙是相同的。

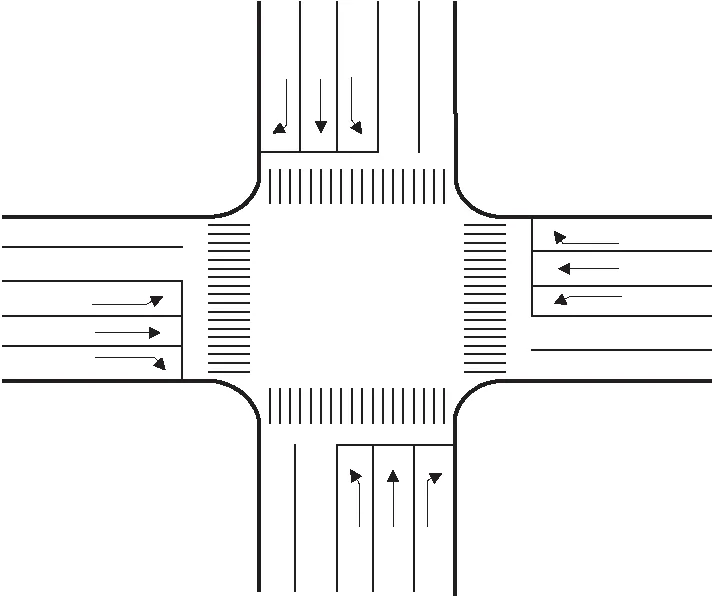
图1 交叉口示意Fig.1 Intersection schematic diagram

2 左转车冲突延误模型

根据基本假定，直行交通流具有优先通行权，不受对向左转车的影响，而左转车则等待直行交通流中出现适当的可穿越空挡驶过冲突点，当穿越空挡不能被利用时，左转车将等待下一个可穿越空挡。阿达姆斯(W.F.Adams)模型是假定主路车流的车头时距为几何分布的基础上推导出来的，而此处的对向直行车流车头时距服从CoWan’s M3分布，笔者根据阿达姆斯延误模型的研究思路[8]计算左转车在冲突点处的延误。

2.1 等待时间的概率密度分布和平均等待时间

直行车车头时距分布概率密度函数为：

f(t)=αλe-λ(t-τ)，t>τ

(1)

现设定次要道路上的车辆到达交叉口后的t时间内能够驶入的概率为V(t)，当车辆到达交叉口不能直接驶入时，(t+Δt)时间内(Δt是微小时间)能够驶入车辆的状态包括以下两种情形：t时间内能够驶入的情形和t时间内不能够驶入但下一个Δt时间内能够驶入的情形。Δt时间内能够驶入车辆，是指Δt时间内主要道路上到达一辆车之后，其后的空挡大于τ的情形。由此可得：

V(t+Δt)=V(t)+[1-V(t)]αλ0Δte-λτ

(2)

式中：λ0为主要道路上车辆的到达率。

但是，由于时刻t时不能驶入车辆，所以此时的直行车车头时距(t-τ)比τ短，车头时距比τ小的车辆到达率，等于空挡长度在区间[τ,2τ)的平均时长的倒数，即：

(3)

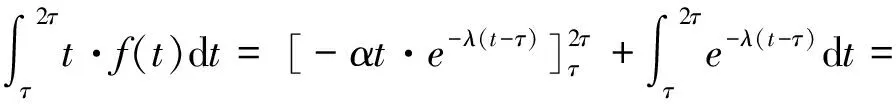
(4)

(5)

主路上直行车辆到达率为：

(6)

由式(2)，当Δt→0时，

(7)

变量分离积分得：

(8)

两边积分得：

V(t)=1-ce-αλ0·te-λτ

(9)

由初始条件V(0)=αe-τ，可得：

c=1-αe-λτ

(10)

因此，

V(t)=1-(1-αe-λτ)e-αλ0·te-λτ

(11)

排队时间的概率密度：

(12)

则平均排队等待时间为：

(13)

2.2 包含交叉口排队等待时间在内的平均延误时间

(14)

因此，左转车在冲突点处的延误为：

(15)

3 数据采集与模型验证

假设车辆从停车线开始不受对向直行车流影响，即有足够可穿越间隙通过时的左转车辆的行驶时间，与车辆在冲突情况下减速行驶或停车等待出现可穿越间隙时驶过冲突点至出口道的时间差记为左转车辆经历的冲突延误。笔者对南昌市孺子路—象山北路交叉口进行了调查，将调查的左转车辆和直行车流量代入式(15)计算得到的左转车辆冲突延误，结合实际观测的左转车辆的冲突延误来计算相对误差，如表1。

表1 左转车冲突延误模型计算值及相对误差

通过多组实际观测和模型计算，得出平均相对误差为8.977%，表明利用模型计算得出的左转车辆冲突延误与实际观测延误的偏差较小，模型具有较高的精度和很好的实用性。

4 结 语

通过假设直行车到达服从Cowan’s M3分布，推导出了直行优先情况下左转车在冲突点处的延误计算模型，最后通过实际调查数据对模型精度进行了验证。该模型对于我国城市道路交叉口的管理和控制具有一定的参考意义和实用价值。

[1] 冯军红,贺尔铭,张文刚.两相位信号交叉口左转交通流延误模型的研究[J].交通信息与安全,2009,27(1):28-31.

Feng Junhong, He Er’ming, Zhang Wengang.Study of a delay model for left-turn flow two-phase signalized intersection [J].Journal of Transportion Information and Safety, 2009, 27(1): 28-31.

[2] 宋现敏,孙峰,王殿海. 两相位交叉口车辆冲突延误模型[J].吉林大学学报:工学版,2009,29(2):326-330.

Song Xianmin,Sun Feng,Wang Dianhai. Conflict delay models at two-phase intersection [J].Journal of Jilin University:Engineering and Technology Edition, 2009, 29(2): 326-330.

[3] 赖元文,荣建,刘小明.基于IQA方法的信号交叉口左转延误计算[J] .武汉理工大学学报:交通科学与工程版,2012,36(2):274-277,282.

Lai Wenyuan,Rong Jian,Liu Xiaoming.Left-turn delay computation at signalized intersection based on incremental queue accumulation [J].Journal of Wuhan University of Technology: Transportation Science & Engineering, 2012, 36(2): 274-277,282.

[4] 李丽丽.信号交叉口左转交通流组织中的临界问题研究[D].长春:吉林大学,2009.

Li Lili.Research on the Critical Question of Left-turn Traffic Organization at Signalized Intersections [D].Changchun:Jilin University,2009.

[5] 杨晓光.直行优先信号控制交叉口左转交通流延误模型[J].同济大学学报:自然科学版,1998,26(3):284-289.

Yang Xiaoguang.Traffic delay model of left-turn flow on signalized intersection with straight-going priority [J].Journal of Tongji University: Nature Science, 1998,26(3): 284-289.

[6] 王殿海,孙锋,金盛.两相位交叉口左转车通行能力计算方法[J].吉林大学学报:工学版,2007,37(4):767-771.

Wang Dianhai,Sun Feng,Jin Sheng.Method of computing left-turn vehicle traffic capacity at two-phase intersection [J].Journal of Jilin University: Engineering and Technology Edition, 2007, 37(4): 767-771.

[7] 马国胜,马万经.两相位交叉口左转交通流冲突延误改进模型[J].哈尔滨工业大学学报,2012,44(10):75-78.

Ma Guosheng,Ma Wanjing. Improved left-turn conflict delay model at two-phase intersection [J].Journal of Harbin Institute of Technology, 2012, 44(10): 75-78.

[8] 荆便顺.道路交通控制工程[M].北京:人民交通出版社,1995.

Jing Bianshun.Road Traffic Control Engineering [M].Beijing:China Communications Press, 1995.