波形钢腹板梁界面滑移计算公式推导
赵瀚玮,韩 西,王 玲
(重庆交通大学 土木建筑学院,重庆 400074)
波形刚腹板预应力混凝土(PC)箱梁结构是一种新型桥梁结构形式。该结构的优点除了能大量减轻自重以外,还因波形腹板的褶皱效应,提高了预应力效率,免除了腹板对上、下混凝土板的徐变、收缩变形的约束作用,其独特的结构形式更适宜布置体外预应力,免除在混凝土中预埋预应力管道的繁杂程序。
波形钢腹板预应力混凝土结构虽然极大优化了桥梁结构的受力,同时也带来了传统混凝土箱梁没有的问题。由于钢波形腹板与混凝土之间通过抗剪连接件共同参与工作,因此混凝土板和钢腹板之间会发生相对滑移。界面相对滑移对结构的刚度,强度均存在影响。关于波形钢腹板梁的抗弯力学性能,万水,等[1-3]做了全面的试验以及理论研究,并提出拟平截面假定理论以分析其截面应力分布;任红伟,等[4-5]阐述了界面相对滑移与预应力作用对波形钢腹板梁的承弯性能的影响,但并没有提出计算界面相对滑移的具体公式。
笔者参考传统的钢混组合梁的界面滑移的理论计算方法[6],对波形钢腹板梁在几种工况下界面滑移沿梁纵向的分布的计算方法进行了探讨。
1 基本假定
波形钢腹板预应力混凝土箱梁因波形钢腹板的褶皱效应,波形钢板受沿梁纵向轴力作用下,将发生极大的轴向变形,即波形钢板沿纵向的实际弹性模量Ex是大大地小于钢材的初始弹性模量E0,这里令之为有效弹性模量[7]。取一个波长的波形钢板,根据卡氏定理,波形钢板在轴向力N作用下的变形为:
(1)

(2)
式中:t为钢板厚度。


图1 轴向力下的波形钢腹板Fig.1 Corrugated steel webs under axial force
笔者只分析1/2箱梁,将模型上混凝土板、波形刚腹板上翼缘板、波形刚腹板下翼缘板、下混凝土板4个部分,计算模型为一简支梁,如图2。图中,l为梁长,用以计算的剪力连接件为栓钉连接件。

图2 简支梁以及组合截面Fig.2 Simply supported beam and composite section
根据以上的分析,有如下假定:
1)波纹钢腹板上、下翼缘与上、下混凝土板之间不发生翘曲,只有纵向滑移。
2)梁的上、下缘钢板和混凝土的平均应变符合拟平截面假定。
3)钢材料和混凝土材料工作时都处于线弹性阶段。
4)梁的弯曲变形是小变形,且忽略剪切变形。
5)钢板与混凝土的界面相对滑移与水平剪力呈线性关系,剪力件刚度不发生退化。
6)抗剪连接件和混凝土间的摩擦力忽略不计。
7)在发生界面滑移之前,抗剪连接件间不存在应力重分布。
2 计算公式推导
取波形钢腹板梁上的某一微段,将4部分弹性隔离体分开来分析,假设微段的4部分有着相同的曲率φ,波形钢腹板上、下翼板受相同大小的竖向力,各弹性隔离体在微段上的受力情况如图3。
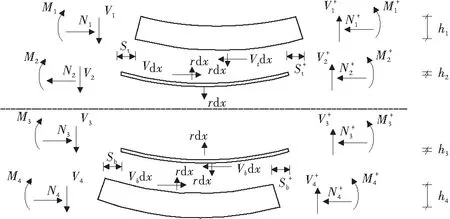
图3 微元体受力Fig.3 Force icon of micro segment
图3中St,Sb为波形钢腹板上、下翼板与混凝土之间的界面相对滑移;单位长度r为各个隔离体之间的挤压力;M,N,V为各弹性隔离体所受的弯矩、轴力、剪力。
在组合梁构件中,4个弹性体满足拟平截面假定,在荷载作用下混凝土与波形钢板具有相同的曲率φ,则有:

(3)
式中:Ec,Es分别为混凝土和波型钢板翼板的弹性模量;I1,I2,I3,I4为截面的惯性矩。
根据曲率相同的假设,可得:
4个弹性体的在竖向弯矩M和轴向力N作用下,滑移界面上的应变为:

(5)
式中:n=Es/Ec;εtc,εts分别为上滑移界面混凝土板和波形刚腹板翼板的应变;εbs,εbc分别为下滑移界面混凝土板和波形刚腹板翼板的应变;A1,A2,A3,A4为各截面计算面积。
从而可得上、下界面的先对滑移应变为:
(6)
式中:εt,εb分别为上、下界面的相对滑移;ht=h1+h2,hb=h3+h4。
对式(6)求变分得:
(7)
根据相对滑移与水平剪力成正比的假设,有:
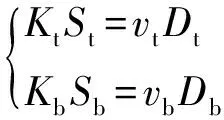
(8)
式中:Kt,Kb为抗剪连接件的抗剪刚度;vt,vb为上、下交界面单位长度内的水平剪力;Dt,Db为上、下交界面抗剪连接件的间距。
根据各弹性体的平衡条件,有力的平衡条件:

(9)
而根据力矩的平衡条件略去小量得 :
由于波形刚腹板的纵向刚度很小,根据假设,波形钢腹板传递竖向挤压力。从而有:
(11)
将式(10)叠加,而后将式(11)代入其中得:
(12)
将式(3)求导后与式(8)一起代入式(12)中得:
(13)
将式(9)、式(13)代入式(7) 中,可得微分方程:
(14)
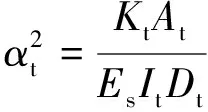
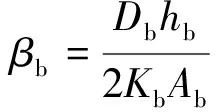
式(14)即为简支波形钢腹板梁在竖向抗弯时的界面滑移的微分方程。由式(14)可以看出,波形钢腹板梁的上、下界面滑移的微分方程的表达式是一样的,只是和上、下缘的截面特性以及剪力连接件的分布形式有关。而在于任何荷载下,滑移微分方程不变,只与剪力V的表达式不同。
3 结果与分析
由前面推导可知,上、下界面滑移的表达式形式一致,为简化分析过程,现假设上、下界面的截面形式以及剪力件分布相同,其微分方程参数都为α,β,然后对各种荷载下的结果进行分析。
3.1 梁受各种荷载作用下的滑移

(15)
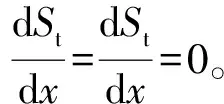
(16)
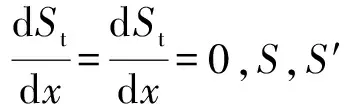
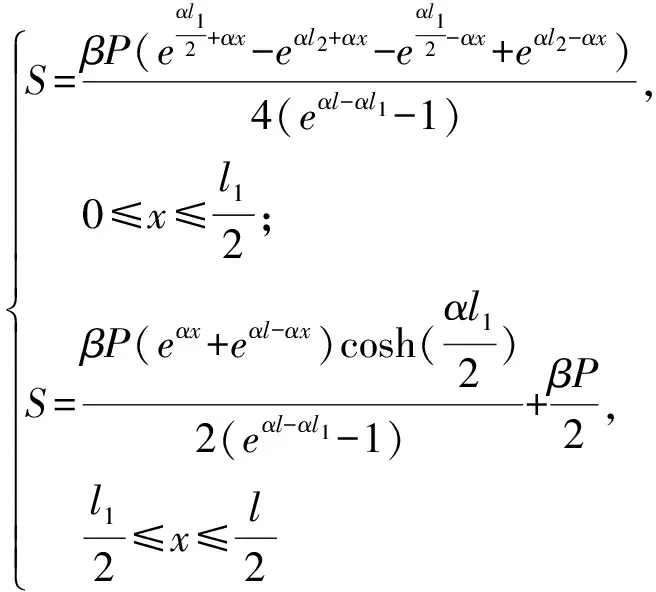
(17)
式中:l2=l-l1/2。
3.2 梁由滑移引起的附加曲率分析
得出波形刚腹板梁上、下界面滑移的解后,将其求一阶倒数即得到界面的滑移应变ε=S′,根据曲率相同的假定,则有:
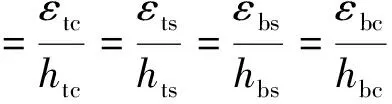
(18)
又因为εt=εtc+εts,εb=εbs+εbc,则有:

(19)
其附加曲率如图4,知道附加曲率过后,就可以通过结构力学原理得出组合梁在一般荷载作用下的附加弯矩。

图4 截面附加应变与附加曲率Fig.4 Additional strain and curvature of section
需说明,由于现在的波形钢板剪力连接件的形式多种多样,式(8)可根据GB 50010—2010《混凝土结构设计规范》或文献[3]自行确定。
通过以上分析可以发现,在不同荷载作用下都有一定滑移的应变。滑移应变以梁中点为向两端发展,并产生梁的附加曲率,进而产生梁的附加弯矩,影响梁的整体抗弯性能。相对于现在仅用换算截面的抗弯性能来评估波形刚腹板梁抗弯能力有了一定进步,但本文并没有考虑预应力的影响。
4 结 语
笔者研究了波形钢腹板简支梁界面相对滑移问题。基于波形钢腹板箱梁所满足的拟平截面假定,不考虑波形钢腹板的抗弯能力,将梁分成4个弹性隔离体进行分析与讨论,得出了梁滑移微分方程,并推导了一般作用下界面滑移的表达式以及附加曲率的表达式。
[1] 万水,陈建兵,袁安华,等.波形刚腹板PC组合箱梁简化计算及试验研究[J].华东交通大学学报,2005,22(1):11-14.
Wan Shui,Ghen Jianbing,Yuan Anhua,et al.Simplified calculation and experimental study of PC composite box girder with conrugated steel webs[J].Journal of East China Jiaotong University, 2005, 22(1): 11-14.
[2] 杨丙文,黎雅乐,万水,等.波形钢腹板箱梁畸变应力分析[J].东南大学学报:自然科学版,2011,41(5):1065-1069.
Yang Bingwen,Li Yale,Wan Shui,et al.Stress analysis of box girders with corrugate steel webs under distorsion [J].Journal of Southeast University:Natural Science, 2011, 41(5): 1065-1069.
[3] 徐强,万水.波形钢腹板PC组合梁设计与应用[M].北京:人民交通出版社,2009.
Xu Qiang,Wan Shui.Design and Application of the PC Composite Beam with Corrugated Steel Webs [M].Beijing: China Communications Press,2009.
[4] 任红伟,刘保东,李鹏飞.考虑剪切滑移的波纹刚腹板预应力箱梁抗弯承载力计算[J].公路交通科技,2012,29(3):86-91.
Ren Hongwei,Liu Baodong,Li Pengfei.Calculation of flexural capacity for prestressed box girder with corrugated steel webs considering shear slip [J].Journal of Highway and Transportation Research and Development, 2012, 29(3): 86-91.
[5] 任红伟.波纹刚腹板预应力混凝土箱梁弯曲性能试验研究[J]. 铁道学报,2008,30(1):61-64.
Ren Hongwei.Experimental study on prestressed concrete box- girders with corrugated steel webs under symmetrical loads[J].Journal of the China Railway Society, 2008, 30(1): 61-64.
[6] 聂建国,沈聚敏,袁彦声.钢-混凝土简支组合梁变形计算的一般公式[J].工程力学,1994,11(1):21-27.
Nie Jianguo,Shen Jumin,Yuan Yansheng.A general formula for predicting the deflection of simply supported composite steel-concrete beams with the consideration of slip effect [J].Engineering Mechanics,1994,11(1): 21-27.
[7] Elgaaly M, Hamilton R,Seshadri A.Shear strength of beams with corrugated webs [J].Journal of Structure Division, ASCE,1996, 122(4):390-398.
[8] 陈宜言. 波形钢腹板预应力混凝土桥设计与施工[M].北京:人民交通出版社,2009.
Chen Yiyan.Design and Construction of Prestressed Concrete Bridge with Corrugated Steel Webs [M].Beijing: China Communications Press, 2009.
[9] 刘磊,钱冬升.波纹钢腹板的受力行为[J].铁道学报,2000,22(增刊1):53-56.
Liu Lei,Qian Dongsheng.Behaviors of corrugated steel webs under loading [J].Journal of the China Railway Society, 2000, 22(S1): 53-56.

