内置式永磁同步电动机电感参数计算分析

石有计

(铁岭师范高等专科学校，铁岭112000)

0 引 言

内置式永磁同步电动机(以下简称IPMSM)具有高过载能力、高功率密度、突出的转矩控制能力、易于弱磁调速而且调速范围宽等优点。因此，在航空航天、新能源混合电动汽车驱动、风力发电、数控加工等领域得到了广泛的应用。

IPMSM的电抗参数是电机设计中的重要参数之一，IPMSM的各种性能指标和力能指标与电机电感参数密切相关。磁路饱和对IPMSM的电感参数会产生很大影响［1－3］，对相关问题很多文献做了大量研究，而研究磁路间交叉耦合作用对电感特性产生的影响方面的文献不多。由于IPMSM具有复杂的转子磁路结构，磁路饱和现象相当严重，并且交、直轴磁场存在交叉耦合作用，使得电感参数难以精确计算，而电感参数对永磁电机的运行特性会产生重要影响。另一方面，随着运行点的变化，实际电机中磁路的饱和程度和磁场分布也会相应发生改变，这会引起电感参数发生改变。而电感参数的不确定性会进一步波及对电机运行特性分析的准确性。鉴于此，本文对永磁同步电动机的电感参数在不同工况下的准确计算方法进行研究。

1 IPMSM 的 d－q 轴数学模型［4－5］

d－q坐标系下磁链传统方程:

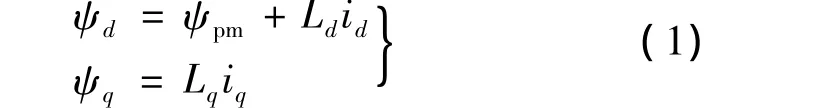
式中:id为d轴等效电流，iq为q轴等效电流;Ld为d轴等效电感，Lq为q轴等效电感;ψd和ψq分别为d轴和q轴等效磁链，ψpm为永磁体产生的磁链。d－q坐标系下电压方程:

式中:Ud和Uq分别为d轴和q轴等效电压;ωr为转子旋转电角速度。

2 电感参数计算模型

2.1 不考虑电机磁路饱和

假设d－q轴完全解耦的情况下，电感计算模型如下:［6］

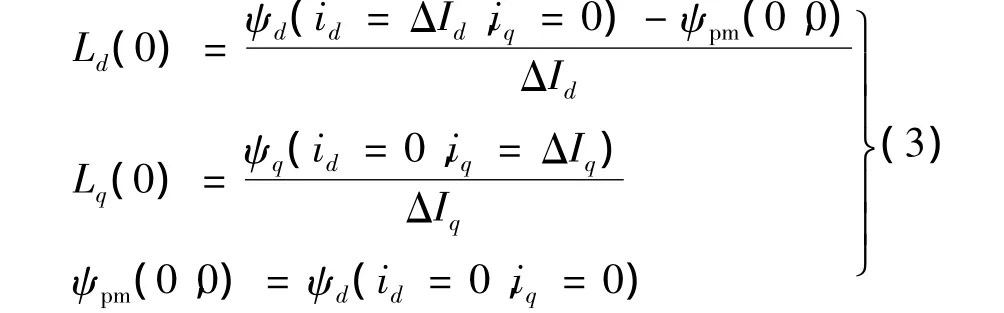
式(3)中的ΔId和ΔIq一般取额定电流的 5%～10%进行计算。

2.2 考虑电机磁路饱和

假设d－q轴完全解耦情况下，电感计算模型:

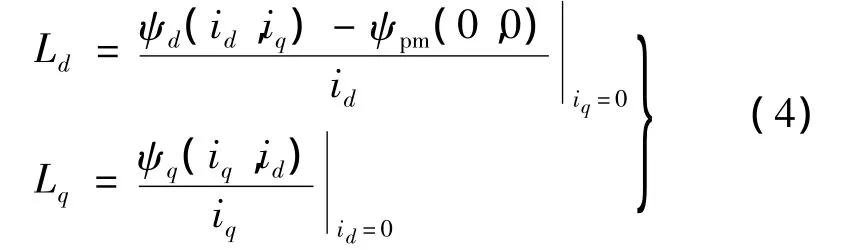
实际上，随着转子铁心的饱和度的变化磁链会发生变化，则计算得到的电感参数也会随磁路的饱和而发生变化。

2.3 考虑交叉饱和的电感计算模型

永磁电机d，q轴磁路存在共同部分，使得d，q轴间存在交叉耦合作用［7－8］。考虑交叉耦合的磁链表达式如下:

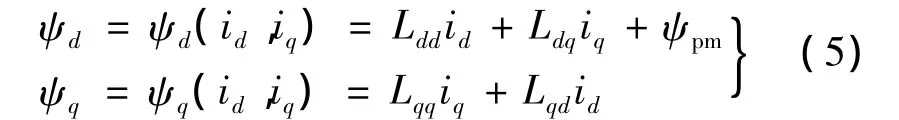
式中:Ldd为d轴自感;Lqq为q轴自感;Ldq和Lqd分别是d和q轴间交叉耦合电感。进一步得到如下电感参数计算模型［9］:

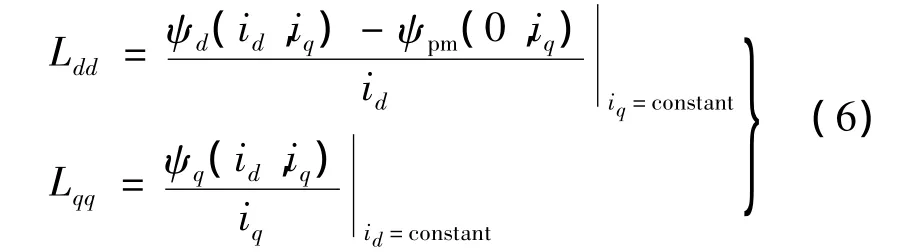
2.4 考虑交叉耦合的修正的电感计算模型

IPMSM的磁场是由永磁体、电枢电流id和iq的共同激励产生的，在d轴去磁电流变化时，电机磁路的饱和程度也会相应的改变。在以下两种情况时，一种是永磁体单独作用，另一种是电流和永磁体共同作用，式(6)Ldd表达式中，电机的饱和程度在两种状况下难以确保相同，因此不能准确地计及交叉饱和对电感参数的影响。若要求得准确的d轴电感，必须使得磁路的磁导率μ在两种情况下不变，这样电机就具有相同的饱和程度。准确计算方法:假设在永磁体和电流共同作用时的磁导率为μ，在保持磁导率不发生变化的情形下，然后去掉永磁体，再加上相同的电流来计算d轴电感值，如下:

3 电感参数的有限元计算与分析

3.1 内置式永磁同步电机有限元建模及主要参数

用Ansoft有限元分析软件创建IPMSM二维有限元瞬态模型如图1所示，其基本设计参数如表1所示。

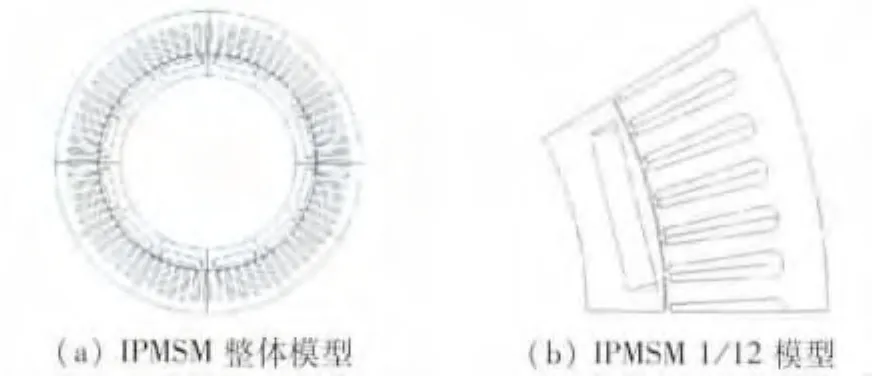
图1 IPMSM有限元模型

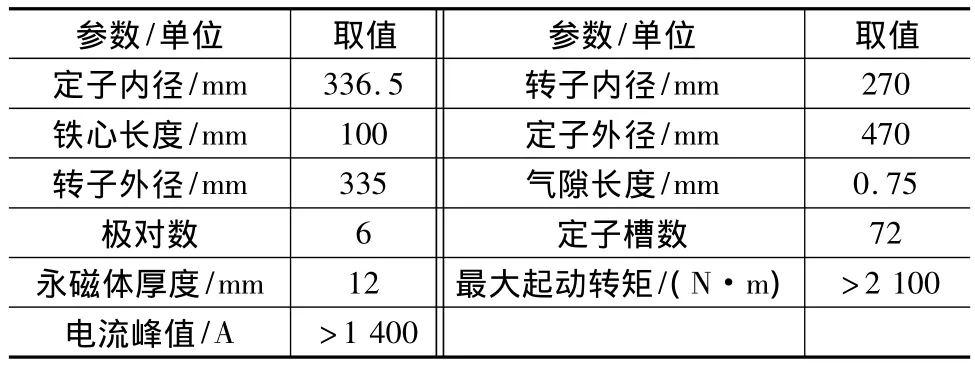
表1 IPMSM设计参数

3.2 计算方法

基于有限元方法，利用 Ansoft软件进行电磁场分析的结果来计算各个电感参数的方法如下［10］:在某一运行点下，求取永磁体磁链ψpm，id，iq共同作用时该运行点的磁导率μ，保持该点磁导率μ不变，然后分别求取id单独作用产生的ψd和ψqd;iq单独作用产生的ψq和ψdq;永磁体单独作用产生的磁链。再通过Ansoft软件处理后得到此时对应的电感参数;对不同运行点进行计算，得到对应于不同运行点的电感参数。该法同时考虑了磁路饱和以及d，q轴磁路交叉耦合对d，q轴电感参数的影响。

电感参数的计算式:

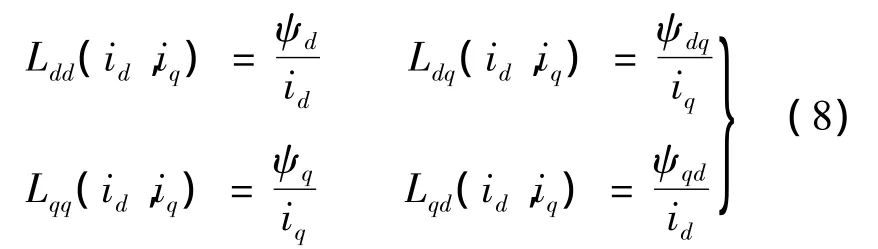
3.3 计算结果与分析

根据所建样机模型，向电机通入不同的定子电流，其范围:id∈(－850，0)A，iq∈(850，0)A。计算得到不同电流下的d轴总磁链ψd和q轴总磁链ψq。

对应某一个q轴电流时，ψd随id的变化如图2(a)所示，对应某一个d轴弱磁电流时，ψq随iq的变化如图2(b)所示。

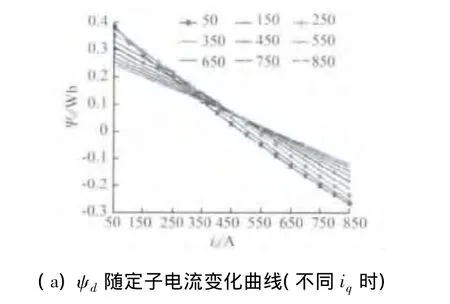
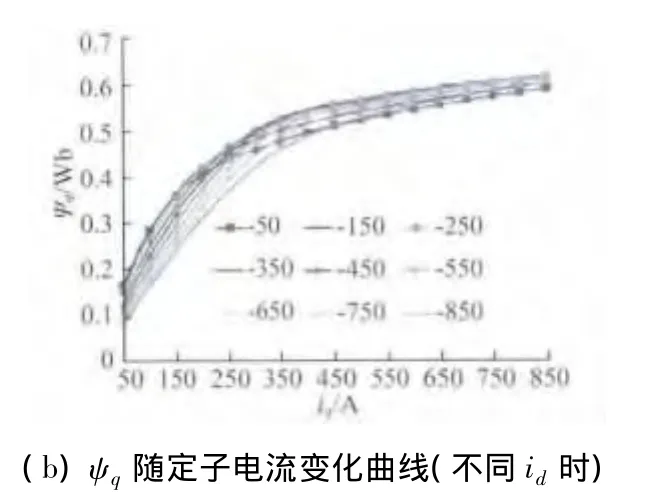
图2 d轴和q轴磁链随定子电流变化图

由图2可以看出，ψd随iq的不同相对变化较大，而ψq随id的不同并没有显著变化。

在得到d，q轴总磁链情况下，保存运行点磁导率不变，从总的磁链中分解出id和iq单独作用产生的磁链，根据式(8)计算得出d，q轴各电感参数随d，q轴电流变化的曲线，如图3和图4所示。

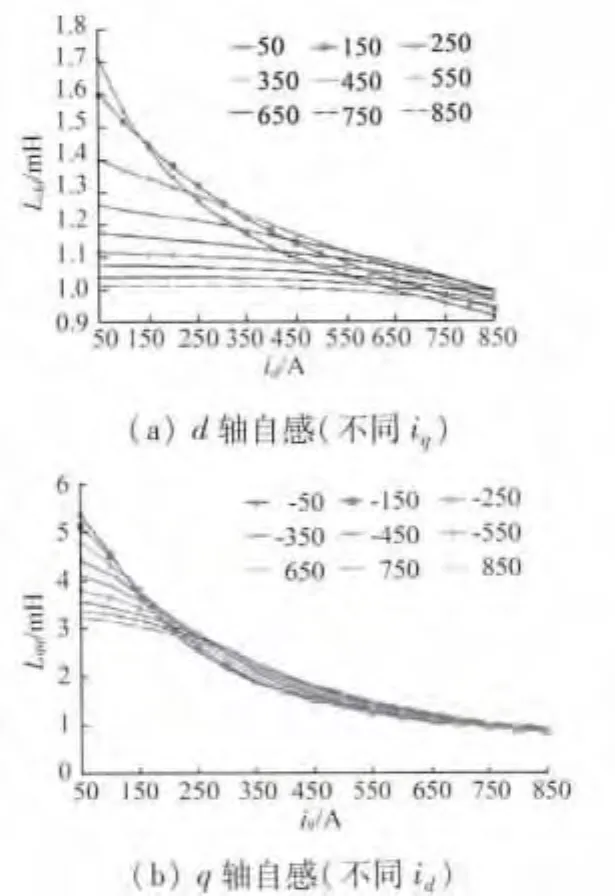
图3 d，q轴自感参数

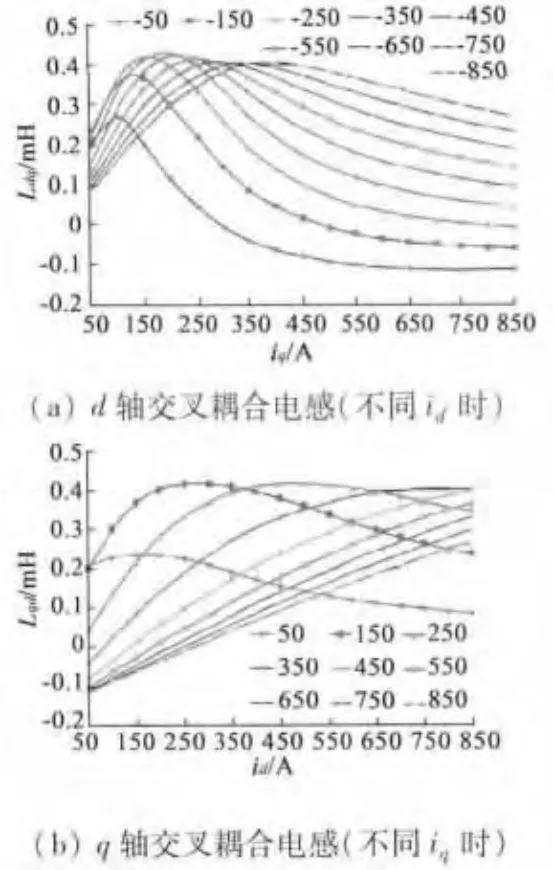
图4 d，q轴交叉耦合电感参数

图3(a)给出了对应不同iq时，d轴自感参数Ldd随弱磁电流id变化的情况;图3(b)给出了不同id时，q轴自感参数Lqq随iq变化的情况。当iq较小(iq＜250 A)时，随着id的逐渐减小，由图3(a)可以看出，Ldd会逐渐增大;由图3(b)可以看出，Lqq也逐渐增大。而当iq增加到一定数值时，id的变化对Ldd和Lqq的影响几乎可以忽略不计，Ldd可看成是常数。而iq增大使Lqq下降较多。由图3整体上看，iq较小时，Ldd约为 Lqq的1/4 ～1/3，iq较大时，Lqq近似等于Ldd的值。Ldd和Lqq随电流的变化不相同的原因是因为d轴磁路不易饱和而q轴磁路饱和。

图4(a)给出了不同d轴弱磁电流时，Ldq随iq变化的情况。由图4(a)可看出，iq发生变化时，对Ldq的影响不大，且当去磁电流id较大时，Ldq值较大。图4(b)给出了不同q轴电流时，q轴交叉耦合自感参数Lqd随id变化的情况。由图4(b)可看出，id的变化对Lqd影响较大，当iq数值较大时，随着去磁id减小，Lqd呈线性减小。总之id和iq对交叉耦合电感都会产生影响，但id影响要大于iq。由图还可以看出，在磁路没有达到饱和状态时，交叉耦合电感数值比较大些，能达到约d轴自感的30%。通过计算表明两种交叉耦合电感值相等:Ldq=Lqd。原因是两种交叉耦合磁链所通过的路径是共磁路区域，磁路饱和度是相同的。而同一饱和度的磁路下，单位电流产生的磁链相同，所以电感相同。

4 实验验证

随着电机磁路饱和程度的变化，电抗参数也随之改变，要准确测量其数值不太容易。本文采用一种间接验证的方法，即应用以下两种参数对电机空载和负载特性分别进行仿真，一种是通过上述计算得到的电感参数(变参数);另一种是不考虑饱和因数时的固定参数(恒参数)，然后与实测结果进行对比。

4.1 空载特性仿真与实测对比

两种不同方法的仿真结果与样机实测的空载特性如图5所示。

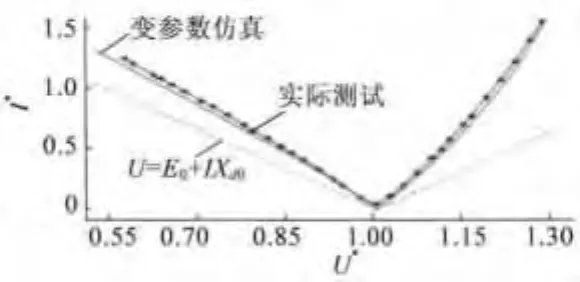
图5 空载特性仿真与实测对比

从图5中可以看出，变参数仿真和实际测试结果吻合度很好，而使用恒参数的仿真结果与实测数据差异较大。

4.2 负载特性仿真与实测对比

两种不同方法的功角特性曲线仿真结果与实测对比如图6所示。

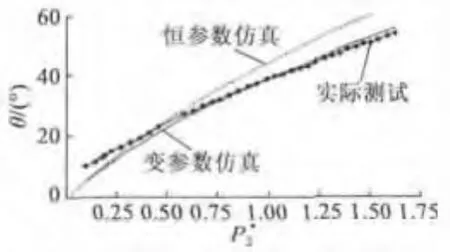
图6 负载特性仿真与实测对比

从图6可看出，相同负载率下，在负载较大时，和恒参数仿真比较，变参数仿真结果非常接近实测值。

5 结 语

本文利用Ansoft二维静态有限元对IPMSM进行电磁场分析的结果显示:在不同运行点，随着磁路饱和程度的变化，永磁体、交直轴电流产生磁链也会随之改变。在不同运行点考虑磁路饱和及交叉耦合，运用保存相对磁导率不变的方法，分析计算了d，q轴自感参数和d，q轴交叉耦合电感参数。结果表明:d轴自感参数随电流变化很小，q轴自感参数由于受到饱和的影响而显著下降，而且交叉耦合电感Ldq和Lqd既受d轴电流id影响，又受q轴电流iq的影响，但id影响要大于iq。并且 Ldq和Lqd值基本相等，在磁路处于不饱和状态时数值相对大些，大约是d轴自感参数的30% ，并随饱和程度逐渐增加而逐渐减小。利用计算得到的电感及永磁磁链参数，通过对样机的空载和负载特性仿真，并与实际测试结果比较，验证了参数计算方法的合理性。

［1］李景灿，廖勇，姚俊.饱和对埋入式永磁同步电机电感特性的影响［J］.重庆大学学报，2009，32(11):1285－1290.

［2］付强，王艾萌，魏亮.磁路交叉饱和对内置式永磁同步电机宽调速控制性能影响的研究［J］.微电机，2011，44(1):40－45.

［3］LEE Ji－Young，LEE Sang－Ho，LEE Geun－Ho，et al.Determination of parameters considering magnetic nonlinearity in an interior permanent magnet synchronous motor［J］.IEEE Trans.on Magnetic，2006，42(4):1303－1306.

［4］PANDA S K，XU Jianxin，QIAN Weizhe.Review of torque ripple minimization in PM synchronous motor drives［C］//2008 IEEE Power and Energy Society General Meeting－Conversion and Delivery of Electrical Energy in the 21st Century.IEEE，2008:1－6.

［5］PETROVIC V，ORTEGA R，STANKOVIC A M，et al.Design and implementation of an adaptive controller for torque ripple minimization in PM synchronous motors［J］.IEEE Trans.on Power Electronics，2000，15(5):871－880.

［6］CHEDOT L，FRIEDRICH G.A cross saturation model for interior permanent magnet synchronous machine.Application to a startergenerator［C］//Proc.of the 39th IEEE IAS Annual Meeting.IEEE，2004.

［7］MORIMOTO S，SANADA M，TAKEDA Y.Wide－speed operation of interior permanent magnet synchronous motors with high－performance current regulator［J］.IEEE Trans.on Ind.Appl.，1994，30(4):920－926.

［8］EL－RERAFI A M，WU J.Determination of the parameters representing thecross－magnetizing effect in saturated synchronous machines［J］.IEEE Trans.Energy Conv.，1993，8(3):333－342.

［9］QI G，CHEN J T，ZHU Z Q.Influence of skew and cross－coupling on flux－weakening performance of permanent－magnet brushless AC machines［J］.IEEE Transactions on Magnetics，2009，45(5):2110－2117.

［10］WALKER J A，DAVID G D.Flux－linkage calculation in permanent－magnet motors using the frozen permeabilities method［J］.IEEE Trans.on Magnetic，2005，1(10):3946－3948.