基于新型算法的永磁电机齿槽转矩削弱方法

李晓宁，吴苏敏，屠新雅，孔德坤

(1.电子科技大学，成都611731;2.南车株洲电机有限公司，株洲412001)

0 引 言

在永磁电机的工作过程中，如果将定子绕组断路，电枢齿便会与永磁体相互作用，产生磁阻转矩，此转矩即为齿槽转矩。齿槽转矩是电机工作过程中产生振动和噪声的主要原因，轻载及低速运行时更为明显，在高性能永磁同步电机的设计过程中，应尽量削弱它。以往的研究分析了电机极弧系数是影响齿槽转矩的重要因素［1］，同时证明了磁体偏心距对齿槽转矩的影响，认为随着偏心距增加，齿槽转矩幅值减小［2］。文献［3］研究了磁钢径向尺寸与齿槽转矩的关系，此外，定转子斜槽与气隙长度也与齿槽转矩有着密不可分的联系［4－5］。抑制电机齿槽转矩有磁极偏移、改变极弧系数、改变磁极磁化方向、磁极偏心、磁极削角、斜槽等［6］，由于斜槽方案在初步设计中已经采用，故本文主要研究永磁电机永磁体厚度、极弧系数、偏心距和气隙长度与齿槽转矩之间的关系。

电机结构参数影响其性能，但影响的高度非线性使得求取其准确目标函数及约束条件的难度变得很大。同时在电机的优化过程中，电磁场有限元数值计算方法求解过程需要大量迭代计算，因此需要结合一定的优化算法来减小资源消耗和优化时间。本文利用支持向量机算法建立电机参数与性能的数学模型，然后利用粒子群算法对其进行寻优，得到4个参数的最佳取值使得电机得到最小的齿槽转矩。

1 电机仿真模型

RMxprt是Ansoft自带的等效磁路法模块，可向2D有限元计算模块中直接导入计算结果并自动生成相应的有限元模型，本文采用Ansoft来完成电机的计算与分析过程。

电机4极36槽，部分参数如表1所示，绕组采用双层Y形接法，长度设为12 cm。为削弱定子绕组谐波，选用短距绕组，第一节距y1=7。同时为减小气隙磁场波动，采用定子斜槽设计。

表1 电机原始参数

生成的电机模型如图1所示。

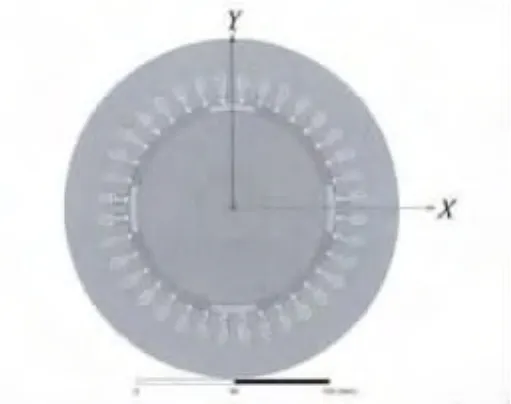
图1 永磁同步电机模型

齿槽转矩是定子绕组断路时产生的，因此需要在建立好的模型中将电源激励设为0。由于磁场储能此时集中在气隙部分，故需要对气隙部分进行网格加密。电机转速设为1(°)/s，图2为生成的齿槽转矩。

由图2中可看出，齿槽转矩与其解析表达式一致，可近似看作正弦波，但此时齿槽转矩较大，约为3.06 N·m，应通过优化算法加以优化。

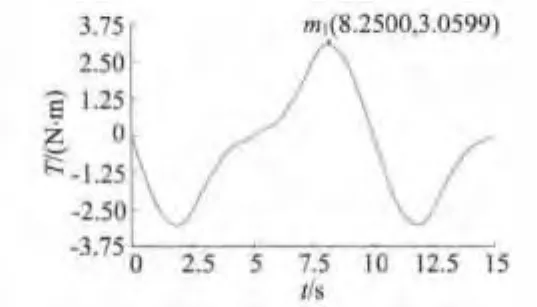
图2 齿槽转矩曲线

2 参数优化过程

2.1 支持向量机回归

支持向量机(SVM)是一种针对有限样本的模式识别问题进行研究的新型机器学习方法，主要分为两大类:样本分类和回归建模分析。为降低高维问题维数及解决非线性问题，SVM引入了核函数，减小了计算复杂程度受问题维度的影响，而变得只与支持向量的个数相关。统计理论中常用的核函数主要有线性核函数、多项式核函数、高斯径向基核函数、指数径向基核函数以及多层感知机核函数5种。由于高斯径向基核函数具有良好的泛化性，所以本文算法中选择高斯核函数。

作为一种具有较强鲁棒性的非参数估计方法，支持向量机回归在电机设计优化中已经得到了成功的应用。彭春华等通过支持向量机算法建立风电机出力与运行参数之间的非线性拟合模型，并基于此模型和风速的变化对风力机桨距角进行优化进而实现了风电机出力最大化［7］。王群京等介绍了支持向量机在电机设计中的一些应用，并对其在永磁球形步进电动机中的应用前景进行了展望［8］。支持向量机回归建模除了核函数的选择，其内容还包括容量误差的选择、损失函数的选择以及与核有关的参数的选择等。

2.2 样本空间建立

参数优化的第一步工作是产生用于非线性电磁建模的输入输出样本数据。本文中，输入为设计变量:永磁体厚度、偏心距、极弧系数与气隙长度，输出为目标函数:电机齿槽转矩。4个设计变量各有5个取值，总共有625次实验。为缩短耗时，采用正交实验设计方法选取实验数据。

正交实验利用设计变量各水平之间的互相均匀搭配，使方案产生的数据点在设计变量空间均匀分布，进而较全面地反映设计变量对系统性能特征的影响规律。通过初步的实验可以确定实验中各变量合理的取值范围:极弧系数0.6～0.85(无量纲)，偏心距1 ～5mm，气隙长度0.6 ～1.2mm，磁极厚度3.5～8mm，依据因数个数和水平个数选择正交表，将各组方案依次输入Ansoft，进行电磁场求解，得到的实验结果即可构成SVM算法的样本空间。实验中各变量的取值如表2所示。

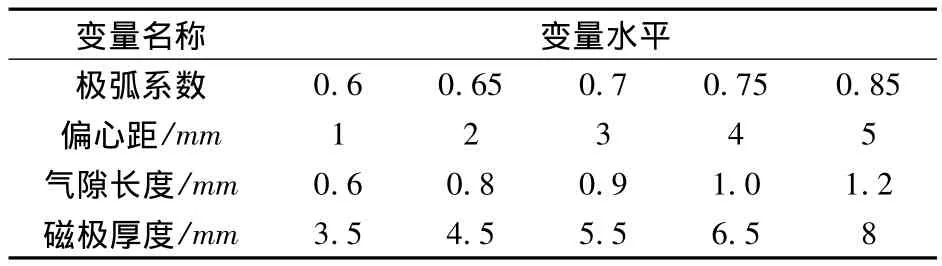
表2 变量水平表

2.3 SVM数学模型建立

最优分类超平面就是SVM算法的数学模型，可以用核函数的代数和表示此超平面:

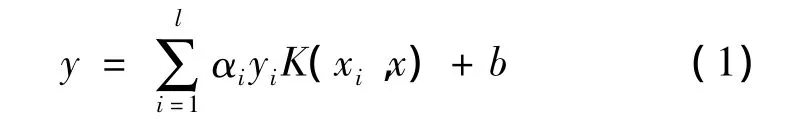
式中:αi为25个样本点中作为支持向量的样本点所对应的拉格朗日常数;K(xi，x)为核函数，支持向量个数则由l表示。从式(1)可看出，欲得到拟合超平面的表达式，需要求取相应的支持向量以及αi。安装libsvm工具箱(林智仁教授等编写)后可以通过MATLAB对模型进行求解。惩罚参数C和核函数参数g是SVM模型的两个关键参数，其值选取会对支持向量机的预测效果产生影响，为得到某种意义下的最优参数，往往采用交叉验证的的思想［9］，可以有效地减少过学习和欠学习状态发生的情况。利用网格搜索算法编写程序，得到C和g的最佳取值，多次调试后得到该问题中的最优参数为C=318.793 2，g=0.03，进而可以得到目标函数的数学模型。

SVM模型预测值与实际值之间的对比如图3所示，三角形代表SVM模型预测的数据，圆圈代表原始数据。

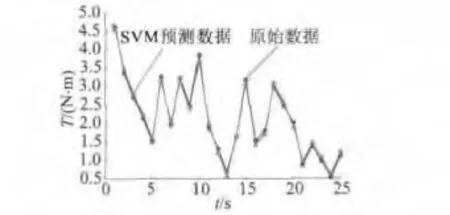
图3 原始数据曲线与拟合数据曲线

2.4 粒子群算法寻优

1995年，Eberhart和Kennedy提出一种群体智能优化算法——粒子群优化(PSO)算法，它的诞生起源于对鸟类觅食过程的研究［10］。PSO算法中，适应度函数对应鸟群与食物之间的距离，每个粒子对应鸟群中的一只鸟，一旦鸟类完成觅食，就代表粒子通过改变自身空间位置而使适应度函数达到了最小值。粒子具有速度、位置以及适应度值三个特征，每个粒子都对应优化问题的一个潜在最优解。粒子的位置和速度是寻优过程中的两个决定性因素，其中个体位置通过跟踪个体极值和群体极值实现更新，而粒子速度则决定了粒子移动的方向和距离，它会随自身及其他粒子的移动经验进行动态调整，从而实现个体在可解空间中的寻优。

对于D维全局优化问题，X=(X1，X2，…Xn)是由n个粒子组成的种群，Xi=(xi1，xi2，…xiD)T代表第i个粒子在搜索空间中的位置，也代表问题的一个潜在解，根据目标函数表达式可计算出每个Xi对应的适应度值。Vi=(Vi1，Vi2，…，ViD)T为第 i个粒子的速度，Pi=(Pi1，Pi2，…PiD)T为粒子个体极值，而Pg=(Pg1，Pg2，…，PgD)T为种群的全局极值。

该粒子迭代后位置:

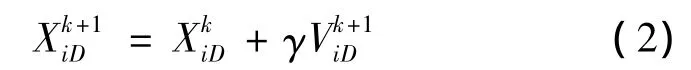
而其迭代后的速度:

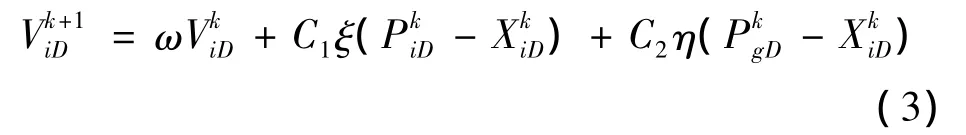
式中:k为迭代数;ω为惯性权重;ξ和η为［0，1］内的随机数;C1、C2为加速常量，分别代表粒子自我认知系数和社会认知系数;γ为速度更新约束因子。PSO算法寻优过程如图4所示。

对于本文的优化问题，将每个设计变量的取值范围作为约束条件，4 个设计变量(x1，x2，x3，x4)作为一个粒子的坐标，SVM预测结果作为适应度函数，利用PSO算法对其进行优化，迭代数为200，种群数量为20，C1和 C2分别设为1.5和1.7，经 PSO寻优后，可得最优点的变量取值:(0.85，4.522 6，0.6，8)。

图4 PSO算法流程图

将优化后的方案代入Ansoft软件，仿真出的齿槽转矩如图5所示。由图5可看出，优化后齿槽转矩为0.314 N·m，相比之前大大减小，仿真结果验证了模型的准确性。

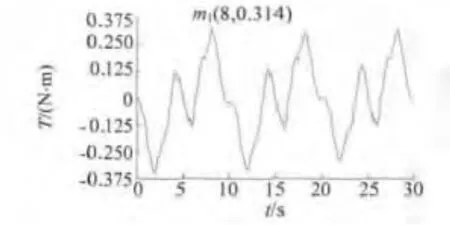
图5 优化后的齿槽转矩曲线

3 结 语

本文从影响永磁同步电机齿槽转矩的因素出发，采用支持向量机方法对其进行回归建模，在此基础上利用粒子群算法对电机的极弧系数、偏心距、气隙长度以及磁极厚度进行优化，通过相对较少的计算，得到了一组使齿槽转矩最小的参数:极弧系数为0.85，偏心距近似为 4.5mm，气隙长度为 0.6mm，磁极厚度为8mm。从优化的有限元仿真结果可知，电机的齿槽转矩由原先的3.06 N·m变为0.314 N·m，大大减小，计算和仿真结果证明了支持向量机在永磁同步电机齿槽转矩优化中的可行性，为电机其他参数的优化过程提供了有效的参考。

［1］杨玉波，王秀和，丁婷婷，等.极弧系数组合优化的永磁电机齿槽转矩削弱方法［J］.中国电机工程学报，2007，26(6):8－11.

［2］秦虹.永磁无刷直流电动机齿槽转矩的削弱［J］.电机技术，2009(12):10－13，18.

［3］周俊杰，范承志，叶云岳.盘式永磁电机齿槽转矩的分析与抑制［J］.机电工程，2009，26(2):79－81.

［4］邓秋玲，黄守道，刘婷，等.永磁电机齿槽转矩的研究分析［J］.湖南大学学报(自然科学版)，2011，38(3):56－59.

［5］王广生，黄守道，高剑.基于Ansoft软件设计分析内置式永磁同步电动机［J］.微电机，2011，44(2):70－73.

［6］张晓宇，王晓远.减少齿槽转矩的无刷直流电机优化设计［J］.微电机，2013，46(1):24－27，40.

［7］彭春华，相龙阳，刘刚，等.基于支持向量机和微分进化算法的风电机优化运行［J］.电网技术，2012，36(4):57－62.

［8］王群京，鞠鲁峰，钱喆，等.支持向量机理论及其在复杂电机设计中的应用［J］.微特电机，2010，(3):67－70.

［9］CAMPBELL C.Algorithmic approaches to training support vector machines:A survey［C］//Proceedings of E－SANN2000.Belgium:D－Facto Publications，2000:27－36.

［10］范坚坚，吴建华，黎宪林，等.永磁同步电动机磁钢的多目标粒子群算法优化［J］.电机与控制学报，2009，13(2):173－178.