槽口偏移对永磁电机齿槽转矩抑制的分析*

谈书志，张 卫，唐 杨，路文开

( 1. 贵州大学 机械工程学院，贵阳 550025； 2. 贵州航天林泉电机有限公司， 贵阳 550003； 3. 国家精密微特电机工程技术研究中心，贵阳 550003)

0 引言

永磁电机结构简单、功率密度高，被广泛应用于医疗器械、航空航天、电动汽车等领域[1]。然而永磁电机本身物理结构会产生 齿槽转矩，对机电性能有较大影响。齿槽转矩是转子永磁体磁场同定子铁心的齿槽相互作用在圆周方向产生的转矩，引起的转矩波动会带来电机的振动与噪声，影响系统的控制精度[2]。随着永磁体的日益广泛使用，齿槽转矩的问题更加突出。如何有效削弱齿槽转矩成为近年来永磁电机研究的热点问题之一。

目前，通过中外学者的研究，在削弱齿槽转矩方面取得了许多重要成果。其削弱方法主要包括，分数槽、极弧系数优化、永磁体分块、辅助槽、斜槽和斜极、磁极偏移、槽口宽优化等。文献[3]分别从极弧系数、偏心距、磁钢厚度角度出发，在优化齿槽转矩同时，降低电机振动与噪声。文献[4]作者用麦克斯韦张量法计算和分析定子表面开槽对齿槽转矩的影响，结果表明辅助槽的相对位置对齿槽转矩有着显著的影响。文献[5]通过在磁极上开不同尺寸的槽来降低齿槽转矩。文献[6]通过在转子上开辅助孔来削弱齿槽转矩。文献[7]将电机每个槽作用下的齿槽转矩波形合成为总的齿槽转矩波形,研究了齿槽转矩的叠加原理。文献[8]则构建6极18槽的样机为研究对象，并将相邻的三个槽口进行不同角度的偏移，以达到减小齿槽转矩的目的，但是没有给出具体的槽口偏移方案。

在上述文献基础上，本文以永磁无刷直流电机为研究对象，提出一种不对称槽口的结构来削弱齿槽转矩。利用ANSYS有限元技术对电机齿槽转矩的叠加规律进行分析验证，在此基础上，通过相邻槽口偏移不同方向的结构来消除齿槽转矩的某次或几次谐波，并用公式计算出最佳的偏移角度。通过仿真验证，表明此方法能对齿槽转矩的抑制起到很好地效果。

1 理论分析

1.1 齿槽转矩的叠加原理

齿槽转矩定义为电机不通电时的磁共能W相对于位置角α的负导数[9]，即;

(1)

根据已有的研究，定子齿不斜槽时电机的齿槽转矩Tcog可以表示为傅里叶级数形式[10]：

(2)

式中，TNSn表示傅里叶级数；α表示定子与转子的相对位置角度；Ns表示电机旋转一周齿槽转矩的波动周期数。其值为永磁体的极数2p和定子槽数Z的最小公倍数。

定子齿不斜槽时单个槽对应齿槽转矩可以表示为傅里叶级数形式；

(3)

式中，Tsci表示单个定子槽对应的傅里叶系数,i为整数。

第k个槽对应的齿槽转矩可以表示为：

(4)

式中，α=2π(k-1)/Z。

由上面的式子可以得到总的齿槽转矩为：

(5)

当2p/z为分数时，转子与每个槽口相对位置不同，每个槽对应的齿槽转矩相位也不同。此时电机总的齿槽转矩就不是简单地单个齿槽转矩叠加而成，而是由不同相位的齿槽转矩正、负两部分叠加之和。

为了研究齿槽转矩的叠加规律，下面分别建立了如图1所示模型；单槽单极、12槽单极、12槽双极、12槽4极和12槽8极。并通过有限元分析软件(ANSYS Maxwell 15)分别分析了不同模型齿槽转矩的波形和幅值。

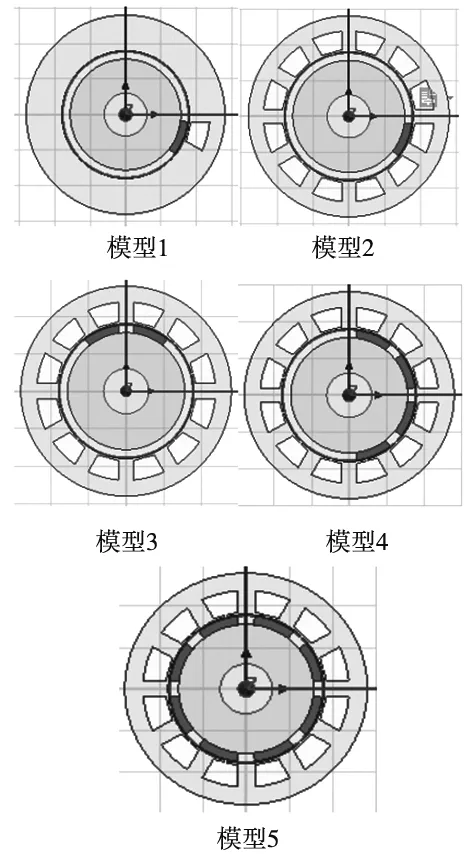
图1 5种模型

由上面的理论可以看出，齿槽转矩的基本部分是由单个槽和单个磁极产生的。整个电机的齿槽转矩是由所有磁极和槽产生的齿槽转矩的基本部分叠加而成的，并且这些基本部分之间是相互独立的。利用有限元分析软件(ANSYS Maxwell 15)分别对模型1和模型2的进行仿真分析，其齿槽转矩的波形图分别如图2和图3所示。从图2可以看出，当永磁体靠近槽口时产生一个正的转矩，当永磁体离开槽口时产生一个负的齿槽转矩，其波形的峰值是0.38N·m。根据齿槽转矩的叠加理论，图3的波形图应该可以由图2波形图叠加得到。从数值理论上分析，用0.38乘以12(槽数)等于4.56N·m应该就是图二的峰值。从图3上我们也发现齿槽转矩的峰值为4N·m。结果相差无几，也验证了上述理论。同时仿真结果也表明，图3的峰值比理论要小，这是因为齿槽转矩的叠加并不是基本部分单纯的简单相加，是由转矩正、负两部分的相位移动叠加而成，这也验证了通过偏移槽口使齿槽转矩波形产生相位移动来削弱齿槽转矩某次或几次谐波方法的有效性和可行性。

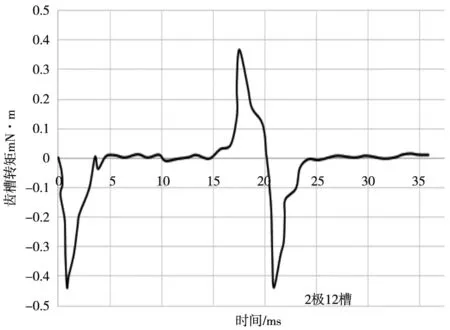
图2 单槽单机齿槽转矩波形图

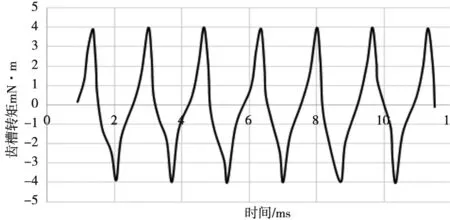
图3 单槽全极齿槽转矩波形图

齿槽转矩值的符号是由定子槽和磁极边的相对位置决定的。因此，永磁体的极性不会影响齿槽转矩的波形。在对称的整数槽电机(相对于分数槽电机而言)中，所有的磁极相对于对称的定子槽结构，其所处的相对位置是相同的，所以每一极所产生的基本齿槽转矩按同相叠加，组成完整的齿槽转矩。下面分别对模型3、模型4和模型5进行仿真分析，如图4所示。从图上可以看到齿槽转矩的峰值4极齿槽转矩略小于2极的两倍，8极的齿槽转矩略小于2极的4倍，这与上述结论相一致。

图4 齿槽转矩对比波形图

1.2 槽口偏移削弱齿槽转矩的理论分析

从上面的理论和仿真分析可知，总的齿槽转矩并不是基本齿槽转矩的整数倍，相邻槽单独作用下产生的齿槽转矩可能是不同相的。通过偏移槽口来改变齿槽转矩的相位，来减小总的齿槽转矩。下面设计一种新型的定子结构如图5所示，使相邻槽口偏移相反的方向。

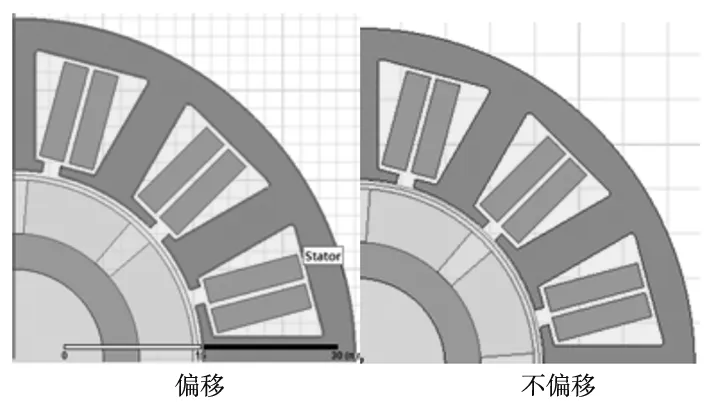
图5 定子结构模型对比图

当槽口向左偏移β角度是，由公式(1)可得齿槽转矩的公式为：

(6)

当槽口向右偏移β角度时，齿槽转矩公式为：

(7)

从文献[11]中提到，电机齿槽转矩可以看作是每个磁极作用下齿槽转矩的叠加。将上面两式相加除以2就是电机总的齿槽转矩。其表达式如下：

(8)

从公式(8)中可以看出，偏移角β总有一个最优值是齿槽转矩Nsn次谐波产生的齿槽转矩为零。即cos(Nsnβ)=0，则：

(9)

2 有限元仿真

为了进一步验证文中槽口偏移方法的正确性及效果，本文用以8极12槽电机为例进行有限元仿真验证。在原有电机结构上不发生变化，只改变定子槽口的偏移方向，使相邻槽口偏移相反的方向，如图6所示。

电机的主要参数见表1。

表1 电机主要参数表

图6 槽口偏移

根据公式(9)最佳槽口偏移角度是3.75°(n=1、Ns=24)。本文分别使定子槽口偏移0°、2°、3°、 3.75°、4.5°、和6°，研究不同偏移角度对齿槽转矩的影响。仿真结果如图7所示。

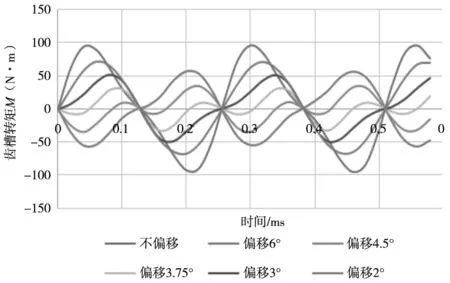
图7 齿槽转矩对比波形图

通过有限元分析表明，当定子槽口发生偏移时，齿槽转矩会得到明显的抑制。同时槽口偏移不同的角度，齿槽转矩的削弱效果也有所不同。

表2 转矩峰值表

可以看出随着槽口偏移角度的增加，齿槽转矩先是减小后增大。当偏移角度为3.75°时齿槽转矩最小，总的齿槽转矩也减少了67%，同时验证了公式(9)的结论。

气隙磁通密度和空载反电势是永磁电机重要的参数，对电机的电磁性能影响较大。图8是槽口偏移前后气隙径向磁密图，图9是空载反电动势对比波形图。由图可知槽口偏移前后的气隙径向磁密基本上没有太多的改变，空载反电动势略微下降5%，依然能保持三相对称性。从图10中电机的空载反电动势基波幅值稍有降低，而高次谐波得到较明显抑制，空载反电动谐波畸变率由9%降低为5%。

图8 气隙径向磁密对比波形图

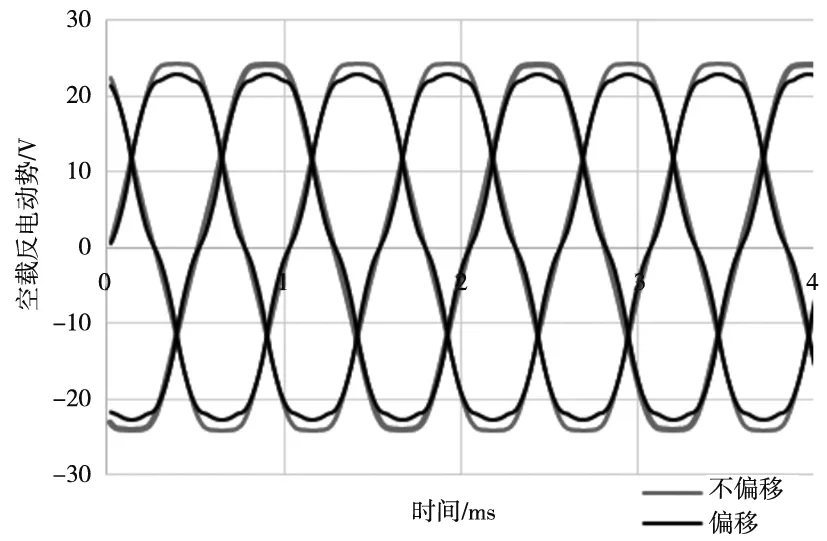
图9 空载反电动势对比波形图

图10 空载反电动势谐波对比

3 结论

本文通过槽口偏移对齿槽转矩的影响的研究，并以8极12槽的电机例仿真验证得到以下结论：

(1)定子槽口左右偏移适当的角度时，能有效地消除齿槽转矩某次或几次谐波，降低总的齿槽转矩。

(2)定子槽口偏移后，空载反电动势基波幅值稍有降低，而谐波畸变率得到很大的改善。同时电机依然保持良好的三相对称性。