双三相永磁同步电动机交互磁饱和模型仿真研究

何新荟，辛小南，齐 歌

(郑州大学，河南郑州450001)

0 引 言

与传统三相永磁同步电动机相比，双三相永磁同步电动机具有以下优点:用低压器件实现大功率输出、减少空间谐波磁势、减少噪声、提高效率、实现可靠性冗余运行［1］。目前研究较多的双三相电机，两套绕组呈30°夹角。但在这种连接方式下，两套绕组之间存在耦合，对电机的控制性能会产生不利影响。为消除耦合的不利因素，本文采用两套绕组呈180°夹角的双三相电机［2］。同时，通常所采用的基于派克变换的d，q轴等效电路模型认为磁路是线性的，即模型中的电感值为常量［1］，从而忽略了电机带负载时磁场饱和的影响。而实际上，由于磁滞影响，d，q轴均存在磁场饱和现象，两轴之间还存在交互磁饱和，所以这种不考虑饱和的电机模型是不够精确的。为改进这种模型，考虑交互磁饱和影响，本文利用MATLAB/Simulink搭建了基于内插外推法的饱和模型，并用仿真实验来验证饱和模型的有效性。

1 考虑交互磁饱和电机模型

对于两套绕组呈180°夹角的双三相电机，两套绕组的空间排列关系如图1所示。采用此绕组分布，可以有效削弱各个相绕组之间的相互影响，增大相绕组自感，减小相绕组之间的互感，尤其是两套三相绕组之间的互感，有利于双三相电机的解耦控制［2］。

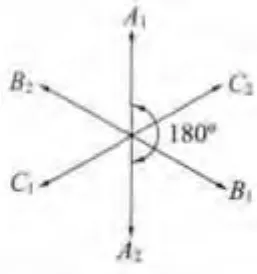
图1 双三相永磁同步电动机定子绕组分布

建立在六相静止坐标系上的数学模型复杂，不利于分析。为简化电机模型，利用转换矩阵T［3－4］，得到两相静止α－β坐标系下的数学模型，然后通过派克变换，得到两相旋转d－q坐标系下的数学模型。

将电机模型从六相静止坐标系转换到α－β坐标系的转换矩阵T为:

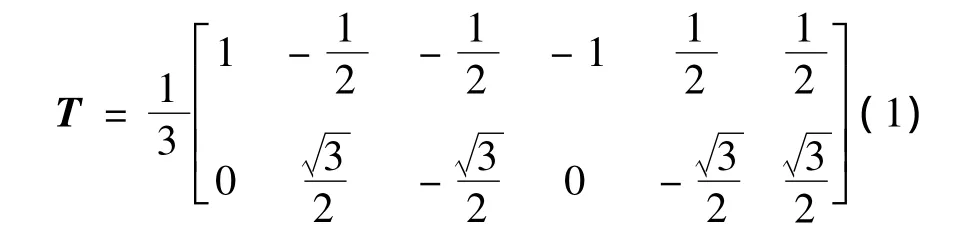
d－q坐标系下电压及磁链方程如下:

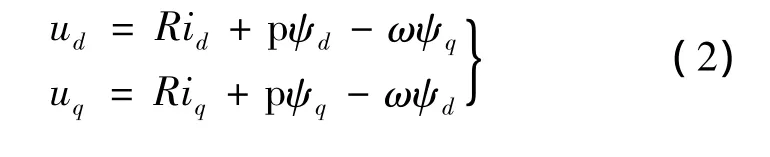
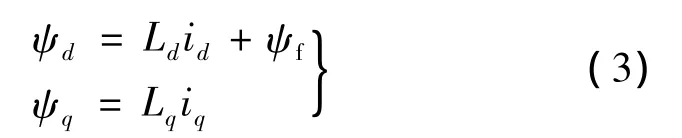
电磁转矩及运动方程如下:

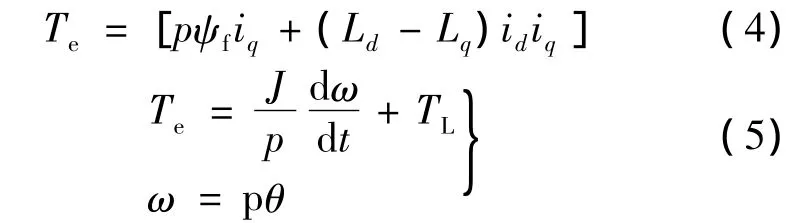
式中:ud，uq为d，q轴定子电压分量;R为定子电阻;id，iq为 d，q轴电流分量;ψd，ψq为 d，q 轴磁链分量;Ld，Lq为 d，q轴电感分量;ψf为永磁体磁链;为微分算子;p为极对数;TL为负载转矩;J为转动惯量;ω为机械角速度。

1.1 d，q 轴交互磁饱和

考虑交互磁饱和法，是在磁链法的基础上，考虑了id，iq对 Ld，Lq的交互影响。故 ψd不仅与 id有关，还受到iq的影响;ψq也同时受到 id，iq的影响。此时磁链方程:

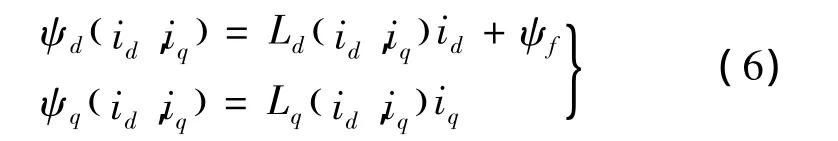
将式(6)代入式(2)、式(4)中，得考虑磁饱和的电压方程及电磁转矩方程:

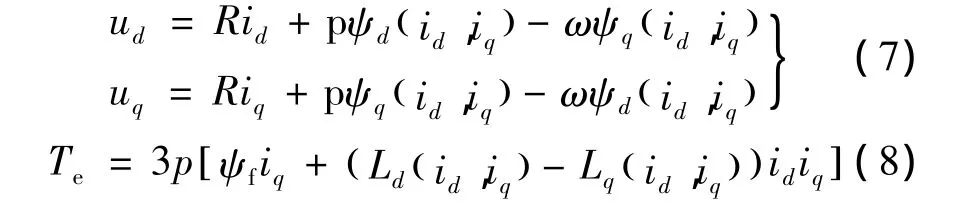
为分析 id，iq对 Ld，Lq的交互影响，文献［2］利用有限元法得到的Ld，Lq与id，iq的非线性关系，如图2所示。

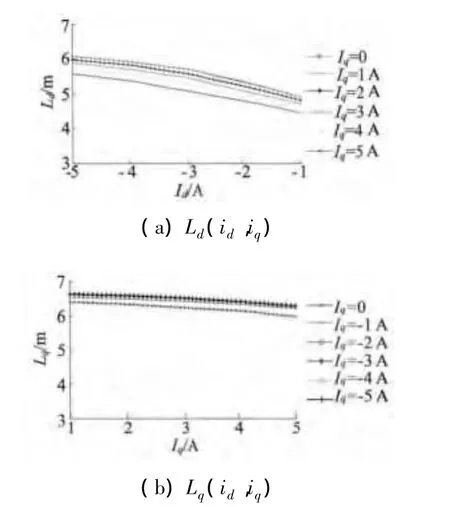
图2 d，q轴电感

电机空载时，输入功率全部转化为电机内部损耗;稳态运行时，电机内部损耗基本不变，故Ld，Lq可近似为常值。当电机负载逐步增大时，输入功率包含电机内部损耗和输出功率，由图可知，id负向增加，去磁作用明显，磁路饱和程度下降，磁导率变大，故Ld增大。考虑交互磁饱和的影响，iq的增加使得d轴磁路饱和程度稍有增加，故Ld有所下降。同时，Lq随着iq的变化不明显，iq增加，Lq略有减小;考虑交互磁饱和的影响，id的负向增加，使得q轴磁路受到影响，饱和程度下降，故Lq随着id负向增加而增大。

1.2 考虑交互磁饱和仿真模型

为反映图2中d，q轴交互磁饱和，利用MATLAB/Simulink建立双三相永磁同步电动机的仿真模型，如图3所示。模型输入为满足图1相角关系的双三相电压、负载转矩TL和永磁体磁链ψf，输出为双三相定子电流、电磁转矩Te和转速n。

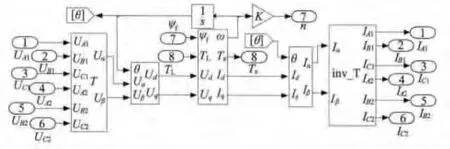
图3 双三相永磁同步电动机仿真模型

根据式(6)、式(7)，可得d－q坐标系下电机磁链和电压模块，模块中id，iq的计算需要使用Ld，Lq的值，而电机的电机参数Ld，Lq与电机的运行状态有关:当电机空载时，Ld，Lq值是常量;当电机带负载运行时，由于磁饱和影响，Ld，Lq由电流 id，iq决定(见图2)。本文采用Switch模块以TL为条件来实现这种转换:当 TL=0 时，Ld=C1，Lq=C2，C1，C2为常量;当 TL＞0 时，Ld=Ld1，Lq=Lq1，而 Ld1，Lq1为满足图2 的函数:Ld1=f1(id，iq)，Lq1=f2(id，iq)。

由于d，q轴电感与电流呈非线性关系，难以写出由 id，iq求解 Ld1，Lq1的解析式 f1，f2。而内插外推法［5］可以通过已观测点数据来估算区域内或区域外未观测点的数据，且效率高、估值准确。为计算Ld1，Lq1的值，本文利用 MATLAB/Simulink中 Lookup Table(2－D)模块，采用两变量的内插外推法建立了 Ld1，Lq1的计算模块。

2 仿真验证

为验证考虑交互磁饱和仿真模型的有效性，将其与不考虑饱和的电机模型在MATLAB/Simulink环境下进行仿真比较。双三相绕组均采用Y接法，主要仿真参数:额定电流5 A，额定电压36 V，额定转速400 r/min，Ld=4.940 3 mH，Lq=6.400 5 mH，p=5，J=0.001 kg·m2，ψf=0.150 37 Wb，TN=5.5 N·m，R=0.419 Ω。

图4分别表示双三相永磁同步电动机不饱和、饱和模型定子电流d，q轴分量在负载转矩TL跃变时的变化曲线，图中虚线表示不饱和模型的id_unsat、iq_unsat，实线表示饱和模型的 id_sat，iq_sat。t=0.3 s 时，TL从0跃变为5.5 N·m。此时，定子电流d轴分量负向增大。对于饱和模型，考虑到交互磁饱和作用，d轴去磁作用明显，磁场饱和程度降低，故饱和模型的id_sat绝对值明显小于不饱和模型的id_unsat的绝对值。同时，定子电流q轴分量增大，由于受到d轴电流的影响，故饱和模型的iq_sat与不饱和模型的iq_unsat相比，增大不明显。

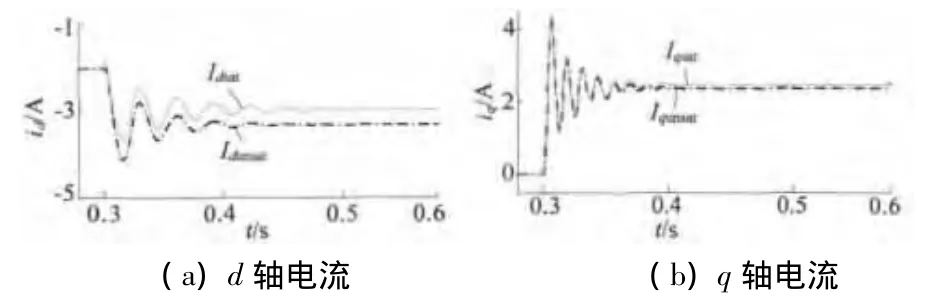
图4 定子d，q轴电流分量

图5为负载转矩跃变时，饱和电机模型的仿真结果。t=0 s时，电机空载，经过0.14 s短时波动达到稳定运行状态，定子电流幅值为2.04 A，电磁转矩为0，转速为额定转速400 r/min。t=0.3 s时，负载转矩跃变为5.5 N·m，经过0.14 s短暂波动，定子电流幅值稳定在3.825 A，电磁转矩达到额定负载转矩，转速恢复为额定转速。

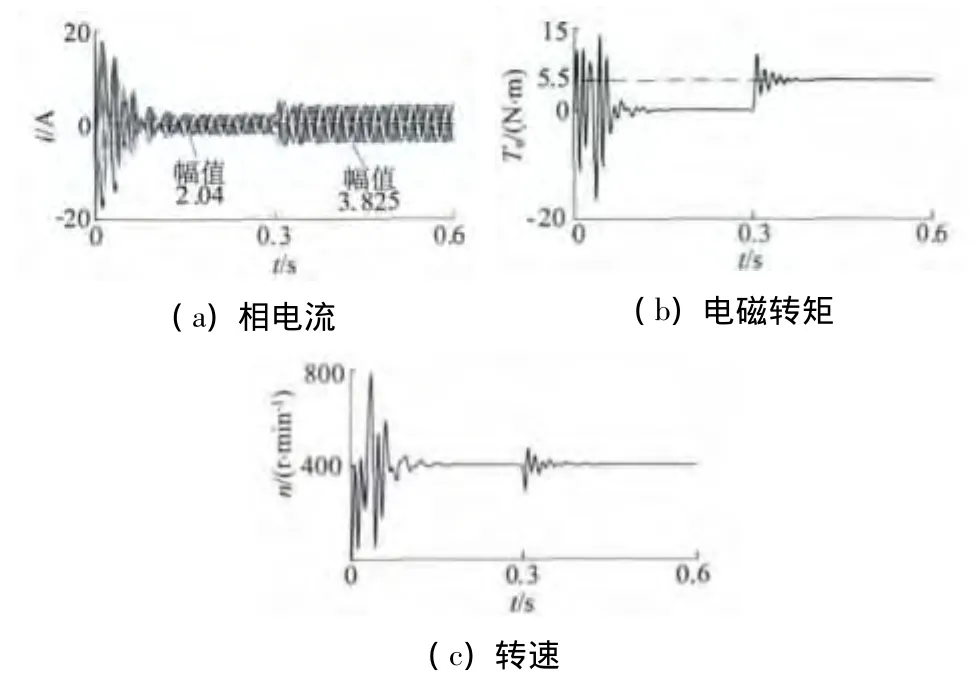
图5 电机饱和模型相电流、电磁转矩和转速

3 结 语

本文通过有限元分析获得电机d，q轴电感与电流的非线性关系，分析了双三相永磁同步电动机d，q轴交互磁饱和的机理。考虑交互磁饱和仿真模型，能够准确反映双三相永磁同步电动机磁路饱和状态下的运行特性，弥补了不饱和模型的不足。本文所采用的建模方法简单直观，同样适用于其他非线性模型的建立。

［1］李崇坚.交流同步电机调速系统［M］.北京:科学出版社，2006.

［2］齐歌.双三相永磁同步电动机交互饱和模型与特性研究［D］.武汉:华中科技大学，2010.

［3］黄进.p对极n相对称系统的变换理论［J］.电工技术学报，1995，(1):53－57.

［4］ZHAO Yifan，LIPO T A.Space vector PWM control of dual three－phase induction machine using vector space decomposition［J］.IEEE Transactions on industry applications，1995，31(5):1100－1109.

［5］熊邺，方大纲，刘铁军.电磁场数值计算中的内插和外推［J］.电波科学学报，2002，17(4):325－329.

［6］杨金波.双三相永磁同步电机驱动技术研究［D］.哈尔滨:哈尔滨工业大学，2011.

［7］李景灿，廖勇.考虑饱和及转子磁场谐波的永磁同步电机模型［J］.中国电机工程学报，2011，31(3):60－66.

［8］景巍，谭国俊，叶宗彬.考虑磁场饱和效应的凸极同步电动机建模［J］.电机与控制学报，2010，14(10):94－99.