基于等效磁路法的永磁同步电机特性分析

李桂丹，宋双利，李 华，李 斌

(1.天津大学，天津 300072；2.国网辽宁省电力有限公司 经济技术研究院,沈阳 110000)



基于等效磁路法的永磁同步电机特性分析

李桂丹1，宋双利1，李 华2，李 斌1

(1.天津大学，天津 300072；2.国网辽宁省电力有限公司 经济技术研究院,沈阳 110000)

针对有限元法在电机设计初期计算量大且耗时长的特点，为8极9槽永磁同步电机提出了一种相对简单且准确的等效磁路法计算模型。模型中把一个永磁体根据磁路分为几部分，给出了考虑永磁体通过定子齿端部产生漏磁时的永磁体模型。该等效磁路网络同时考虑了磁路饱和、齿槽效应和电枢反应等现象。永磁体漏磁不进入电枢绕组，对绕组磁链和电枢反电势并不起作用，因此在模型中把该漏磁单独考虑。通过迭代的方法，来求解铁心磁导。采用节点磁位法来求解该模型网络，得到电机的磁场分布。在此基础上对电机绕组磁链、电枢反电势和齿槽转矩等特性进行分析计算。同时建立了2D有限元模型，对电机磁场和特性进行分析。最后将等效磁路法模型和有限元模型得到的结果进行对比，验证了等效磁路模型的正确性。

等效磁路法；有限元法；永磁同步电机；齿槽转矩

0 引 言

近年来，永磁同步电机由于具有效率高、功率密度大等优点，在工业领域应用广泛[1-2]。特别是分数槽集中绕组永磁同步电机，其端部绕组短、功率密度大、铜耗小、嵌线成本低、转矩波动小[3]，备受国内外研究人员关注。在永磁同步电机的设计和特性分析过程中常用有限元分析法，有限元法分析的结果虽然准确，但是计算量大且耗时长，不适合用于电机设计初期和优化设计阶段[4-5]。等效磁路法也是一种常用且有效的方法，并且很好地协调了计算精度和计算时间之间的问题。最初的等效磁路法模型中只考虑了永磁体和气隙磁导，模型过于简化导致磁场分析的结果并不精确[6]，所以后来研究人员在等效磁路法模型中考虑了漏磁、电枢反应、磁路饱和以及齿槽效应等现象。文献[7]给出了定子无槽时永磁体通过气隙产生的气隙漏磁模型，使得电机气隙磁场密度的分布结果有所提高。文献[8]没有结合具体的等效磁路网络，但给出了对于定子开槽时永磁体通过定子齿端部产生的漏磁模型。文献[9-10] 把一个永磁体根据磁路分成几部分，通过圆弧和直线的磁通路径对齿槽效应进行建模，并且给出了当考虑磁路饱和时，通过迭代来求解铁磁材料磁导率的方法，磁场分布结果较为准确，但该模型网络的结构会随着定转子的相对运动发生变化且模型复杂。文献[11]提出了变网络等效磁路模型，根据定转子相对位置的不同，将1个转子极距划分为可能的10个区间。在不同的区间建立不同的等效磁路网络模型，使得求解过程变得复杂。

目前对基于等效磁路法永磁同步电机分析模型的研究主要是对于各种现象的建模。这样虽然使分析模型的准确度有所提高，但是等效磁路网络的建立和求解过程也变得复杂，因此研究人员在寻求一种相对准确且简单的等效磁路网络模型。

本文针对分数槽集中绕组永磁同步电机给出了一种相对简单且准确的等效磁路网络模型。该等效磁路网络考虑了漏磁、磁路饱和、电枢反应和齿槽效应等现象，所以提出的等效磁路网络模型相对准确。在该模型中把一个永磁体根据磁路分成几部分，同时给出了永磁体通过定子齿端部产生漏磁时的永磁体模型。把漏磁部分单独考虑，且该模型的网络结构不随相对运动发生变化，因此该网络的建立和求解相对简单。在磁场分析的基础上，求解电机磁链、电枢反电势，并利用侧向力法(Lateral Force Method,LFM) 求解电机齿槽转矩。建立2D有限元模型，将计算结果与有限元结果进行对比，验证了提出模型的正确性。

1 等效磁路模型

图1为8极9槽永磁同步旋转电机结构示意图，三相绕组如图1(b)所示采用分数槽集中绕组的分布方式，每相绕组的三个线圈采用串联的连接方式。

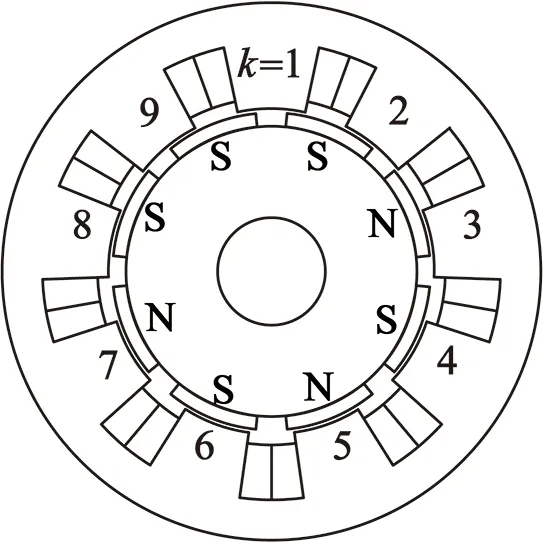
(a) 剖面图

(b) 绕组连接方式

1.1 永磁体模型

电机的漏磁现象如图2(a)所示，在一个齿槽距内永磁体产生的磁通通过定子齿端部回到相邻永磁体，并不进入定子绕组，这部分的磁通对电枢磁链和电枢反电势不起作用。当定转子相对位置如图2(b)所示，在一个齿槽距内S极永磁体产生的磁通部分通过定子齿端部回到N极，部分通过定子齿进入等效磁路网络，对电枢磁链及反电势有一定作用。当定转子相对位置如图2(c)所示，在一个齿槽距内只有一个永磁体，这时永磁体产生的磁通全部进入定子齿。

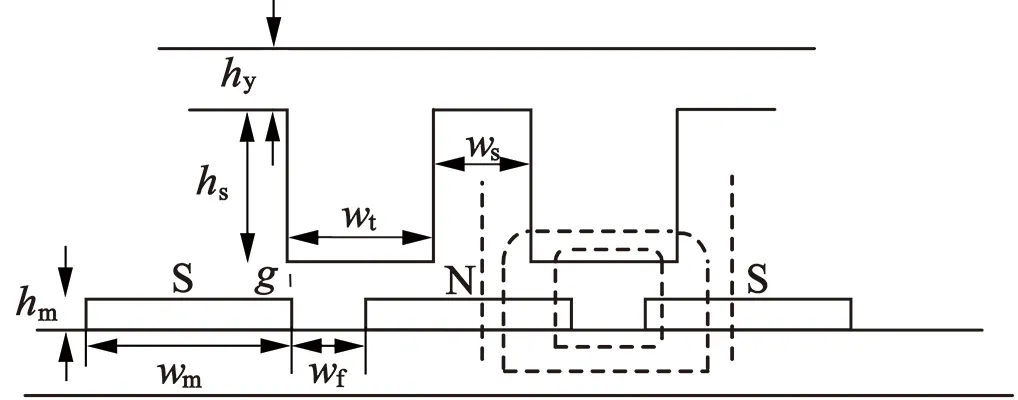
(a) 全部漏磁

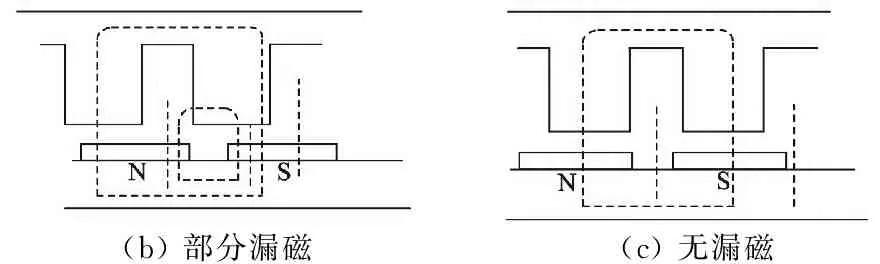
(b)部分漏磁(c)无漏磁

图2 永磁体的产生漏磁示意图

一个齿槽距内永磁体等效磁路模型如图3所示，则x定义：

式中：x表示在一个齿槽距内永磁体进入定子齿的有效宽度；τu为齿槽距；wf为两个永磁体之间的距离；min(XN,XS)表示N极永磁体和S极永磁体在一个齿槽距内的永磁体宽度的最小值；wm表示永磁体宽度。

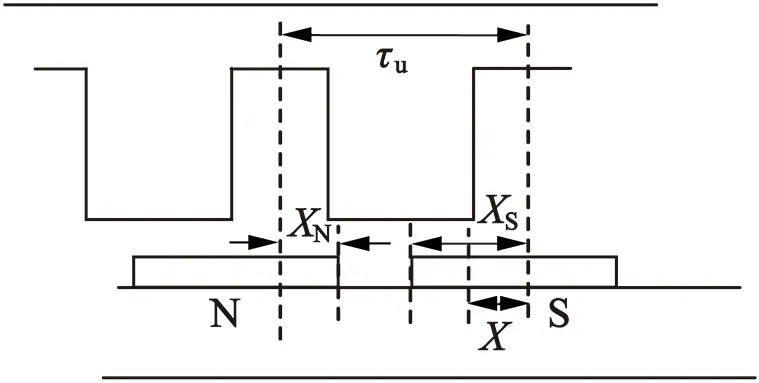
图3 齿槽距内永磁体模型

1.2 永磁同步电机等效磁路法模型

等效磁路法模型如图4所示。以定转子任意一个相对位置为例，永磁体产生漏磁不进入定子绕组单独考虑。根据图1所示的绕组连接方式，电枢绕组产生的磁动势：

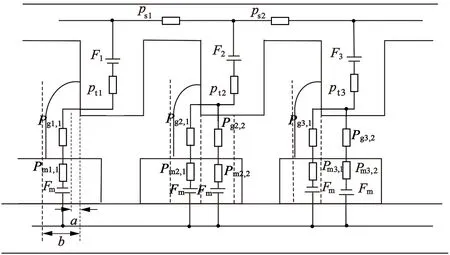
图4 永磁同步电机等效磁路法模型

式中：Fk表示电枢绕组在第k个定子齿上的磁动势，n表示电枢绕组匝数，iu,iv,iw表示每相相电流。

定子部分磁导为：

式中：μ0为气隙磁导率;L为电机深度;wt为电机齿距;hS为定子齿高度;hy为定子铁轭高度。μi为定子铁心相对磁导率，由于考虑磁路饱和，μi并不是常数，需经迭代计算来确定。通过求解等效磁路网络得到每个定子齿的磁密，查磁化曲线得新的磁导率。重复这一过程直到所得的结果误差小于给定值为止[9-11]。

把一个齿槽距内的磁路分为3部分，定子齿的左边、右边和定子齿的正下方。左边和右边的磁路取到槽距的一半，磁力线由直线和圆弧构成[9]，这样在定转子相对运动的过程中等效磁路网络不需要重新建立，只有磁路中的参数变化。磁路参数：

式中：a,b为磁力线与定子齿的距离(如图4所示);μr为永磁体相对磁导率;Hc为永磁体矫顽力;hm为永磁体高度。

2 模型求解

2.1 等效磁路网络求解

当定转子的相对位置确定后，等效磁路网络的参数可以通过计算得到。根据磁路与电路相似，采用节点法求解等效磁路网络，则：

式中：m为节点数，F(k)表示在节点k处的磁动势，φ(k)表示流入节点k的等效磁通源的代数和，当k1=k2时，p(k1,k2)为连接到节点k1的各磁路磁导的总和；当k1≠k2时，p(k1,k2)为连接到节点k1和节点k2的各磁路磁导之和的负数。

节点k1和节点k2之间的磁路如图5所示，则：

φ=p[F(k1)-F(k2)+F0]

式中：p表示节点k1与节点k2之间磁路的磁导;F0表示为磁动势，F(k1),F(k2) 为节点k1和节点k2处的磁动势;φ为磁路的磁通;B表示磁路的磁密;A表示磁路截面积。

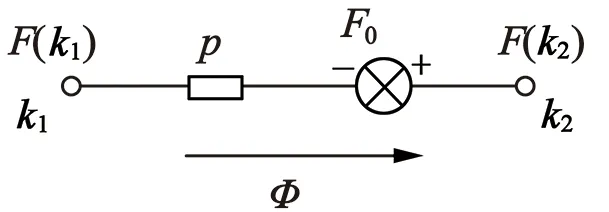
图5 节点之间磁路示意图

2.2 永磁体漏磁求解

永磁体漏磁模型如图6所示。

图6 永磁体产生的漏磁模型

其中，pgN,pgS表示气隙磁导，pmN,pmS表示永磁体磁导。为了使漏磁模型简单且容易求解，不在考虑定子齿端部的磁导。该模型中的磁通和磁密可由下式得到：

式中：φl表示永磁体漏磁磁路的磁通，Bl表示漏磁磁路的磁密，Al表示漏磁磁路通过的截面积。

3 特性分析

3.1 磁链

通过对等效磁路网络的求解，可以得到每个定子齿中的磁通，则每相磁链：

图7为由有限元法和等效磁路法得到U相绕组磁链，两种方法分析的结果基本吻合，等效磁路法得到的结果比有限元法略大，在可以接受的范围内。

图7 U相磁链随转子位置的变化

3.2 反电势

反电势可以由磁链求导得到：

图8为由等效磁路法和有限元法得到的U相绕组反电势，图中取等效磁路法得到的反电势的基次谐波。由图可见，两者结果相当接近。

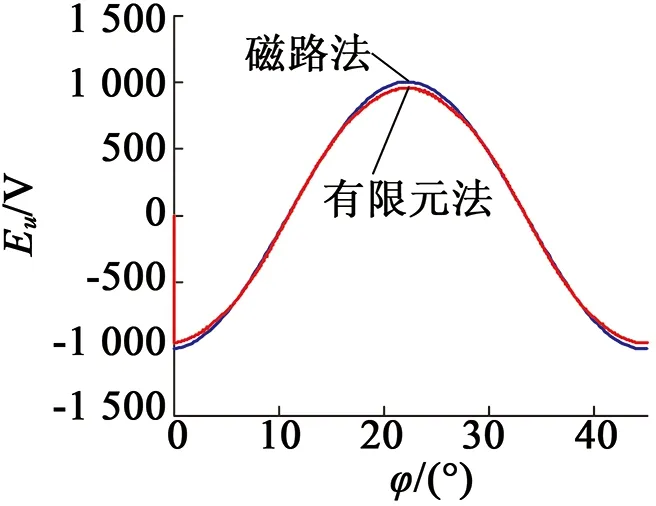
图8 U相反电势随转子位置的变化

3.3 齿槽转矩

齿槽转矩是永磁电机特有的问题之一，永磁电机绕组不通电时永磁体和定子铁心之间相互作用产生的转矩，是高性能永磁电机设计和制造中必须考虑和解决的关键问题。LFM通过进入定子齿侧面的磁通密度来求解齿槽转矩，只需要一个方向的磁通密度分量[12]，则齿槽转矩为：

式中：Bi1,Bi4分别表示第i个定子齿左边和右边磁路的磁密；bi1,ai1分别表示第i个定子齿左边磁路边界到该齿的最远和最近的距离；bi4,ai4分别表示第i个定子齿右边磁路边界到该齿的最远和最近的距离。

图9为有限元法和等效磁路法得到的齿槽转矩的对比结果，从图可以看出，两种方法得到的结果基本吻合，这说明了所建立的等效磁路模型是正确的，具有较高的精度。

图9 齿槽转矩随转子位置的变化

4 结 语

本文为永磁同步电机基于等效磁路法提出了一种简单、准确的计算模型，在该模型中把一个永磁体根据磁路分成几部分，给出了考虑永磁体通过定子齿端部产生漏磁时的永磁体模型。该等效磁路网络中同时考虑了磁路饱和、电枢反应和齿槽效应等。由于考虑了磁路饱和现象，所以采用迭代方法计算铁心磁导。把永磁体漏磁跟等效磁路网络分开求解，这样即使得模型简单，同时结果准确。在电机磁场分析的基础上，求解电枢磁链、反电势，并采用LFM对电机的齿槽转矩特性进行分析。最后通过有限元模型的分析结果与等效磁路法模型结果进行对比，验证了所建立的等效磁路法模型的正确性。

[1] YEO H-K,LIM D-K,WOO D-K,et al.Magnetic equivalent circuit model considering overhang structure of a surface-mounted permanent-magnet motor[J].IEEE Transactions on Magnetics,2015,51(3):1-4.

[2] 司纪凯,刘志凤,司萌,等.一种新型转子永磁同步电机磁场分析及特性[J].煤炭学报,2013,38(2):348-352.

[3] AYMAN M.EL-Refaie.Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges[J].IEEE Transactions on Industrial Electronics,2010,57(1):107-121.

[4] XU Liang,LIU Guohai,ZHAO Wenxiang,et al.Analysis of new modular linear flux reversal permanent magnet motors[J].IEEE Transactions on Magnetics,2015,51(11):1-4.

[5] ZHU Y-W,LEE S-G,CHUNG K-S,et al.Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM[J].IEEE Transactions on Magnetics,2009,45(6):2863-2866.

[6] RAHMAN M A,LITTLE T A,SLEMON G R.Analytical model for interior-type permanent magnet synchronous motors[J].IEEE Transactions on Magnetics,1985,21(5):1741-1743.

[7] TSAI Wen-Bin,CHANG Ting-Yu.Analysis of flux leakage in a brushless permanent-magnet motor with embedded magnets[J].IEEE Transactions on Magnetics,2001,35(1):543-547.

[8] QU Ronghai,LIPO T A.Analysis and modeling of air-gap and zigzag leakage fluxes in a surface-mounted permanent magnet machine[J].IEEE Transactions on Industrial Applications,2004,40(1):121-127.

[9] KANO Y,KOSAKA T,MATSUI N.Simple non-linear magnetic analysis for permanent magnet motors[J].IEEE Transactions on Industrial Applications,2005,41(5):1205-1214.

[10] KANO Y,KASAKA T,MATSUI N.A simple nonlinear magnetic analysis for axial-flux permanent-magnet machines[J].IEEE Transactions on Industrial Electronics,2010,57(6):2124-2133.

[11] 王蕾,李光友,张强.磁通反向电机的变网络等效磁路模型[J].电工技术学报,2008,23(8):18-23.

[12] ZHU Z Q,HOWE D.Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors[J].IEEE Transactions on Magnetics,1992,28(2):1371-1374.

Characteristic Analysis of Permanent Magnet Synchronous Motor Based on Equivalent Magnetic Circuit Method

LIGui-dan1，SONGShuang-li1，LIHua2，LIBin1

(1.Tianjin University，Tianjin 300072，China; 2.State Grid Liaoning Economic Research Institute,Shenyang 110000,China)

An accurate yet simple analytical model for 8-pole/9-slot permanent magnet synchronous motor (PMSM) was presented based on equivalent magnetic circuit method in order to overcome the shortcomings of time-consuming and great computation of the finite element method.The permanent magnet (PM) pole was divided into several sections and the PM model was given when considering the leakage fluxes of the PM through the end of the stator tooth in the analytical model.The magnetic circuit saturation, slot effect and armature reaction were also considered.The leakage fluxes of the PM fail to flow through the stator windings and have no influence on the flux linkage and the back electromotive.Therefore, it was considered independently.The permeance of the core was obtained through the iteration.The nodal analysis was employed to solve the magnetic circuit.Based on the analysis of magnet field, the flux linkage, the back electromotive force, and the cogging torque were obtained.The finite element model was established to analyze the characteristics of the PMSM.The results obtained by the analytical model are compared with the results obtained by 2D finite-element method to verify the validity of the analytical model.

magnetic circuit method (MEC); finite-element method (FEM); permanent magnet synchronous motor; cogging torque

2016-01-05

TM351

A

1004-7018(2016)09-0054-04

李桂丹(1975-),女,博士,副教授，研究方向为电力电子技术及应用、网络分析与综合。