用虚设零点法解函数极值问题
浙江省绍兴鲁迅中学柯桥校区 田 萌 (邮编:312030)
解决有关函数极值问题,一般都是通过求导函数的零点求出极值点来实现,然而,有些时候这一招却不灵啦,请看下例:
例1 已知函数f(x)=ax2-2x+lnx有两个极值点,证明:f(x)的极小值小于-.
分析 第一步:求定义域.函数f(x)=ax2-2x+lnx的定义域为(0,+∞).
第二 步:求 导.f′(x)= 2ax-2+
第三步:求极值点.
令g(x)=2ax2-2x+1,函数f(x)=ax2-2x+lnx有两个极值点的必要条件是g(x)=2ax2-2x+1=0当x>0时有两个不等实根.

设此时2ax2-2x+1=0的两根为x1、x2,且x1<x2.
当0<x<x1时,g(x)>0,即f′(x)>0,f(x)在(0,x1)上单调递增;
当x1<x<x2时,g(x)<0,即f′(x)<0,f(x)在(x1,x2)上单调递减;
当x>x2时,g(x)>0,即f′(x)>0,f(x)在(x2,+∞)上单调递增.

第四步:求极小值.
怎么办?
设f′(x)的零点为x2,则2ax22-2x2+1=0,
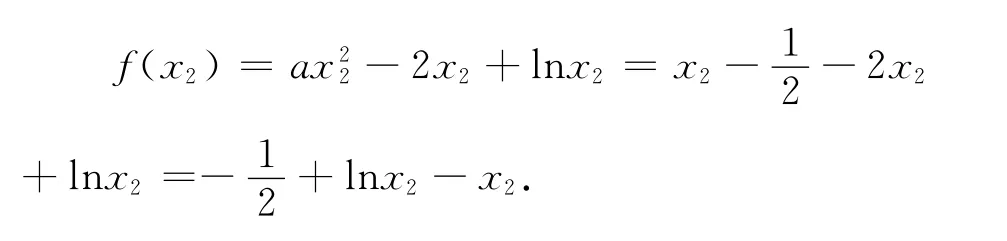
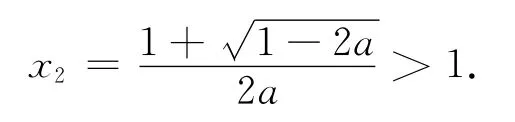
令h(x)=lnx-x,h′(x)=-1.x>1时,h′(x)<0,h(x)在(1,+∞)上是减函数,所以当x>1时,lnx-x<-1,由此.
故f(x)的极小值小于-.
下面再看两个例子.
例2 已知函数f(x)=x3-x2+axa(a∈R).若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
分析 三次函数f(x)的图象与x轴有且只有一个交点等价于:
①函数单调且函数值不同号;②函数极大值小于0或极小值大于0.
因此,求导,得f′(x)=x2-2x+a,
因 △ =4-4a=4(1-a).
① 若a≥1,则△≤0,所以f′(x)≥0在R上恒成立,所以f(x)在R上单调递增.
又因为f(0)=-a<0,f(3)=2a>0,所以f(x)在(0,3)上有零点.
所以,当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
②若a<1,则△>0,
所以f′(x)=0有两个不相等的实数根,不妨设为x1、x2,(x1<x2).
当 - ∞ <x<x1时,f′(x)>0,f(x)在(-∞,x1)上单调递增;
当x1<x<x2时,f′(x)<0,f(x)在(x1,x2)上单调递减;
当x>x2时,f′(x)>0,f(x)在(x2,+∞)上单调递增.
所以f(x)在x1处取值极大值,在x2处取得极小值.
于是应该有f(x1)<0或f(x2)>0.
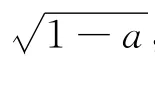
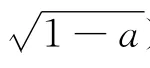
怎么办?用虚设零点法.
一方面,因为x1、x2是方程f′(x)=0的两根,所以x1+x2=2,x1x2=a.

令f(x1)·f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0,
故当0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).

例3 给定函数φ(x)=x2-2tlnx(t>0),t为何值时,方程φ(x)=2tx有唯一解.
解 记G(x)=φ(x)-2tx=x2-2tlnx-2tx,则函数G(x)的定义域为(0,+∞).若方程φ(x)=2tx有唯一解,即G(x)=0有唯一解.
G′(x)=2x--2t=(x2-tx-t),令G′(x)=0,得x2-tx-t=0.
因为t>0,x>0,
当x∈ (0,x2)时,G′(x)<0,G(x)在(0,x2)上是单调递减函数,
当x∈ (x2,+ ∞)时,G′(x)>0,G(x)在(x2,+∞)上是单调递增函数,
故x=x2时,G′(x2)=0,G(x)min=G(x2).
因为G(x)=0有唯一解,故G(x2)=0.
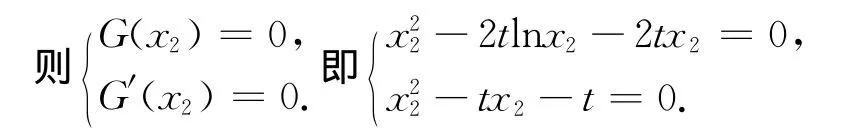
所以2tlnx2+tx2-t=0.
又t>0,故2lnx2+x2-1=0 (*)
设函数h(x)=2lnx+x-1,因在x>0时h(x)是增函数,故h(x)=0至多有一解.

故t=时,方程φ(x)=2tx有唯一解.
从上面三个例子不难看出,“虚设零点法”对于解决一些涉及极值问题的难题很有作用,希望上述例子能给大家以启发,掌握此法.

