插上数学思想的翅膀——从《反比例函数的图象、性质与应用》教学片段谈起

江苏省无锡市第一女子中学 蔡晓华 （邮编：214002）

数学教育有两大视角：教学观和数学观.一度认为，教学法是指导数学课堂教学的重要方针.然而，随着对数学课堂的观察与反思的深入，却越来越意识到教师对数学思想的认识在数学课的设计中的影响也是至关重要的.本文试着从笔者执教的一节公开课《反比例函数的图象、性质与应用》的教学片段，来阐述这一观点.

教学片断

师：我们怎样画出反比例函数y＝的图象呢？

师：我们学过一次函数，让我们用研究一次函数图象的方法来试试，那么怎样画出一次函数图象呢？

生：列表、描点、连线.

师：好的，先列表.首先取x、y的一些对应值，列入表格.可以取原点吗？为什么？

生：不能.因为分母x≠0.

师：是的.那么，图象会落在那些象限？为什么？

生：第一、三象限.因为反比例函数y＝中，x＞0时，y＞0；x＜0时，y＜0.

师：是的.也可以看到反比例函数y＝中，xy＝6＞0，也就是x、y同号.点（x，y）在第一、三象限.既然x≠0，就分别研究x＞0和x＜0.那么我们先来看第一象限.

师：比如取x＝1，x＝3，则y＝6，y＝2.描出点（1，6）、点（3，2）.然后连线.用什么线相连？

生：直线.

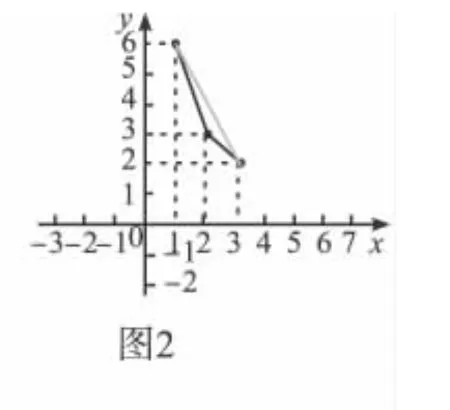
师：我们在x＝1和x＝3之间取x＝2，则y＝3.即点（2，3）.我们把它画上去，发现并不在线段上.（停顿了会）那么是否要连成折线？再取x＝1.5得点（1.5，4），发现还是不在刚才连好的折线上；随着x的无穷取值，想象一下，各点应连成怎样的线？

生：曲线.

师：是的，应以光滑曲线顺次连接.（在屏幕上逐步投影图1－4，并在曲线的曲字上加重语气）

师：这个曲线怎样向右延伸呢？继续取符合反比例函数y＝的数组（x，y）即一系列点（4，1.5）、（5，1.2）、（6，1）、（7），描出这些点，怎样连接？

生：（齐答）光滑曲线.

师：随着曲线向右延伸，曲线上的点有怎样的特点？

生：向下延伸.

师：是的，曲线上的点向右、向下延伸.那么它会与x轴相交吗？

生：会.

生：不会.因为与x轴相交的点的纵坐标为0，而y＝中y≠0.

师：是的，从y＝可知，x＞0时，y总是＞0；而且随之正数x的增大，y不断减小.也就是说，曲线不断靠近x轴，但不与x轴相交.

（投影结论，并将“靠近”、“不相交”两处重点显示）

生：向上、向左延伸

生：曲线越来越靠近y轴，但不与y轴相交.

师：是的，你能从解析式解释这一现象吗？

生：因为x≠0，所以曲线不会与y轴相交.

生：因为y＝中，随着x的减小，y增大.

师：注意这些点的横坐标的范围.（停顿一下）x＞0时，x越小，y越大.也就是说，在第一象限，曲线越来越靠近y轴，但与y轴不相交.

这样，我们可以概括为一句话：在第一象限，曲线越来越靠近坐标轴，但与坐标轴不相交.（图5）.（投影结论，并将“靠近”、“不相交”两处重点显示）

师：现在来考虑当x是负数时，它所对应的y的值也是负数，点落在第三象限，同样的方式，可以作出反比例函数在第三象限的图象.

（动画显示x＜0时相应所取的一组点）同学们用手指着屏幕一起来画一下.（全体学生一起动手.）

师：不错，同学们画得有模有样的.能不能将图象画成“弯弯的月亮，两头翘”？（边说边用手指演示，形如图6，但不投影在屏幕上）为什么？

生：不能.因为曲线是越来越靠近坐标轴.

师：能不能把第一、三象限的两支曲线连接起来，（边说边用手指演示，形如图7，但不投影在屏幕上）为什么？

生：不能.因为x≠0，y≠0，所以不能与x轴有交点.

师：是的，两支曲线是不连的，间断的.从曲线的延伸方向看，当x＞0时，曲线在x轴上方，y轴右侧，并向右、向下延伸不断靠近x轴；向左、向上延伸不断靠近y轴.当x＜0时，曲线在x轴下方，y轴左侧，并向左、向上延伸不断靠近x轴；向右、向下延伸不断靠近y轴的.两支曲线与坐标轴不断靠近而不相交.

师：反比例函数y＝图象是分布在第一、三象限的两支曲线，这样的图象叫做双曲线.（图8）

曲线越来越靠近坐标轴，与坐标轴不相交.让我们再用手指着屏幕画一次.（图8）

教后反思

1 以无限逼近的数学思想为立意，揭示数学知识发生发展的过程

反比例函数的图象与性质是继一次函数之后，学生第二次接触对函数的研究.因此，对于反比例函数图象的研究过程，应类比于一次函数图象的研究，这体现了函数学习的一般方法.从描点作图——观察图象 —— 分析图象特征 ——确定函数中变量x、y之间的“变化规律”，从而得出函数的“特性”的过程，是学习初等函数时不可或缺的，也是后续研究二次函数等其他函数所采用的研究“模式”.同时，在运用“类比”的方法研究时，还有一个“对比”的问题，也就是反比例函数与一次函数之间的“差异性”，如“直”与“曲”，“连续”与“间断”，“和坐标轴相交”与“渐近”.这些在方法上、结论上的异同就是教学设计时考虑如何实现突破的关键点.

另一方面，尽管对于用列表描点画函数图象的方法，学生已经学过，但因当时处于函数学习的初始阶段，学生只是了解了用描点法画函数图象的“三步曲（列表、描点、连线）”，学生对每步要求的理解并不深刻.画反比例函数时，常遇到如下的问题：

（1）“列表”时，选取x时数量太少，难以发现函数图象的特点，有时易忽略x≠0的条件；

（2）“连线”时，学生容易受一次函数的影响而产生负迁移，把反比例函数图象画成折线；

（3）对双曲线与x轴、y轴“越来越靠近（但不相交）”的趋势不易理解.

因此教学时，就特别注意进行有针对性的引导，注意从解析式的分析入手，让学生先进行“数”（x≠0，y≠0，k≠0）、“式”（解析式中x、y的反比例关系）的分析，进而过渡到对“形”（图像）的认识.这就是贯穿这一课时始终的“数形结合”.分析x、y的对应关系，从2个点所连线段到第3个点、第4个点的检验，即通过两点的中间点始终不在线段上的事实，促使学生的思维发生第一次跳跃 ——从“直”到“曲”.再分析x、y的对应关系，由于x≠0，因此自变量x在x＝0处会发生跳跃，那么图象也就要分别在x＜0，x＞0两个方向去逼近x＝0，由自变量的无穷取值，促使学生的思维发生第二次跳跃 ——从“连续”到“间断”，从“一条直线”到“两支曲线”.这就是贯穿上述案例的“由有限到无限”的逼近思想.即列有限个数组，描有限个点，然后分析趋势，借助对无限的合理想象，生动地展示了函数图象的“再创造”.这个过程中，学生完成对反比例函数图象的两次突破就显得顺理成章，合情合理了.

2 以丰富的表象操作经验为依托，实现数学概念从“过程”到“对象”的转化

数学概念具有二重性，即作为“过程”的概念和作为“对象”的概念.在过程阶段表现为一系列的步骤，有操作性，相对直观，容易仿效.比如反比例函数图象的作图过程.但是由于步骤的前后次序以及每一步中包含不少细节，如果停留在过程阶段，思维所考虑的因素呈序列动态，就不易全面掌握，较难抓住要害和实质.当概念进入对象状态时，便呈现一种静态结构关系，易于整体把握性质，并可转变为可被操作的“实体”.只有在此时，一个完整的理解才真正成型.数学思维、理解的认知过程都是要经由“过程”到“对象”的先后顺序，而要实现这个转变，离不开学生的数学实践与体验.

在上述教学片段中，首先是对第一象限中一个个点的具体操作，分析出函数图象的一些特征；然后在第三象限中用手指画示意图，同时完成一些典型错误的辨析，最后是概括出整体性质.这样的教学设计，让学生经历了布鲁纳所说的抽象概念依次发展的3个阶段：动作操作（列表描点）、表象操作（手指描草图）、符号操作（看到反比例函数就想到双曲线），强调了学习经验的积累，促进了学生对反比例函数图象作为一个整体对象的建构.

众所周知，正例有利于建立概念，反例有利于辨别概念.因此，当做出第一象限内的函数图象之后，学生已有了“正例”，类比地，不难在第三象限描出正确图象.继而，再构造两个“反例”，演示而不投影，既可达到辨析概念的目的又尽量不留负面印象.这样，通过丰富学生对数学概念的表象操作，可以促进学生对数学的理解.

3 以函数各种表示形式的沟通为桥梁，建构和完善良好的数学知识结构

函数的表示形式有三种：解析式、表格、图象，这三者是等价的，分别从式、数、图三个方面对函数进行描述.然而，无论教、学，往往重视解析式与图象，而轻视表格，上述教学片段也明显地重视解析式与图象的相互印证，而将表格只是作为作图的准备工具而已，这是基于执教者对函数各表示形式之间的孤立、片面的理解.现在想来，函数的表格形式也是大有教学价值的.一是描点之前的列表，正是将解析式“翻译”为表格，作图只是将表格中的数对“翻译”为坐标系中的点；二是观察分析函数性质时，除了分析函数解析式、观察函数图象外，当然也可以从表格的数据中得到呼应.

比如，针对学生对双曲线与x轴、y轴“越来越靠近（但不相交）”的趋势不易理解的这个问题，就可以充分利用函数的表格形式.让学生观察最终所得的表格（表格一），提出一组问题：

表格一

（1）x＞0时，函数值的符号怎样？x＜0呢？你能用一句话概括吗？

这个现象与图象的什么性质相一致？

（2）x＞0时，随着x的增大，函数值怎样变化？随着x的减小，函数值怎样变化？

这个现象与图象的什么性质相一致？

（3）x＜0时，上述（2）的问题怎样回答？能用一句话概括吗？

通过这组问题的回答与分析，学生得以从“数”的角度直观地体会反比例函数的增减性.

遗憾的是，由于笔者在教学设计阶段尚未认识到函数的表格形式的价值，而错失了这一对反比例函数增减性进行数值的直观的描述的机会.

从这节公开课中，笔者深深地体会到，执教者对相关数学内容的理解越深刻，他（她）的数学课堂才能更有数学味，更悠远、更简练.插上数学思想的翅膀，令数学课堂更有活力.

1 刘金英，李庆.“反比例函数的图象与性质”（第一课时）教学设计与反思［J］.中国数学教育，2011，1、2合订本

2 李士锜.熟能生巧吗？［J］数学教育学报，1996，（8）

3 黄兴丰，汤炳兴，龚玲梅等.经验教师数学课堂教学策略的个案研究.数学教育学报［J］.2012，（1）