构造中间曲线加强不等式
湖南省长沙市第十五中学 厉 倩 (邮编:410007)
2012年辽宁高考文科压轴题如下(见例1):
证明(Ⅰ)当x>1时,f(x)<(x-1);

如果令l(x)=(x-1),φ(x)=(x-1),那么在定义域内f(x)≤φ(x)≤l(x)恒成立,本文我们把这样的曲线φ(x)称为f(x)与l(x)的中间曲线.φ(x)与f(x)具有相同的凸凹性,具有相同的切线l(x).一般的,如果f(x)是复杂的(超越)函数,φ(x)可以是比较简单的(初等)函数,并且符合要求的中间曲线φ(x)的个数较多.这些特点给我们命制鲜活的题目提供了一个新的生长点,也为我们的教学研究提供了一个新的视角.对于例1的第(Ⅱ)小题有当x≥25时,f(x)>(证明略),以下只研究中间曲线.
例2一般化,有如下例3:

令t=,则变形可得h(x)=2t7-t6+(4n-2)t5-2nt4+2(mn+m-3n)t3-n2t2-2n2t=t(t-1)[2t5+t4+(4n-1)t3+(2n-1)t2+3n2t+2n2](这里利用了).
因为x>0,则t>0,又n≥,则2t5+t4+(4n-1)t3+(2n-1)t2+3n2t+2n2>0,
当x=1,则t=1,h(x)=0,有g′(x)=0,
当0<x<1,则0<t<1,h(x)<0,有g′(x)<0,g(x)单调递减,
当1<x,则1<t,h(x)>0,有g′(x)>0,g(x)单调递增.
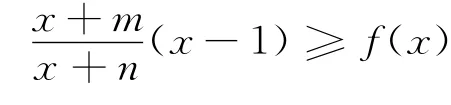
证明 只证左边不等式(右边易证),

令t=,则变形可得h(x)=t3(t4+2t2+9)-2t(t4+2t2+1)-t2(t4+2t2+1),
h(x)= (t-1)(t6-2t3+3t2+2t).
因为x>0,则t>0,
当0<t≤1时,2t-2t3≥0,t6+3t2>0,则t6-2t3+3t2+2t>0,
当t>1时,t6-2t3+1≥0,3t2+2t-1>0,则t6-2t3+3t2+2t>0.当x=1,则t=1,h(x)=0,有g′(x)=0,
当0<x<1时,则0<t<1,h(x)<0,有g′(x)<0,g(x)单调递减,
当1<x时,则1<t,h(x)>0,有g′(x)>0,g(x)单调递增.

仿上可证(略).


