浅谈一类高考解析几何试题的命题途径——由2011江苏、2012辽宁、湖北卷解几题有感
江苏省建湖高级中学 刘友明 (邮编:224700)
解析几何问题以其独特的魅力活跃在每年的各大省份及全国的高考试卷中,且常常以压轴题,拉分题自居,深得出卷人的青睐,是考查学生处理数与形问题能力的一块良土.学生常因数据处理能力不足,出错率较高,无法顺利完成解答,在“数与形的转化”,找“几何关系特征”,“化简计算”等环节有很大欠缺,进而丧失了信心.那么如何才能帮助学生建立自信,并对解析几何问题产生浓厚兴趣呢?前提就是要求老师能在此方面作一些研究,探寻一条解几问题命题的规律及途径,当然这就对教师提出了更高的要求.以下本人就近两年考题作一些研究,以期能与读者共勉.


1 课本及各大省份的考题背景是产生考题的一块热土——研究、探索、推广考题是我们的方向
1.1 学会变换图形的位置 —— 力求能对问题从一个角度出发达到多方位的效果,从而可以提高学生的变位思考能力.
按照德国大数学家克莱茵的观点,我们所研究的几何图形的种种性质,只不过是研究几何图形在各种几何变换下的不变性和不变量.通过感知和学习图形的变换,不仅有助于学生从运动变化的角度去认识事物,去了解图形之间的联系,从而发展他们的几何直觉,而且还能有利于学生感受,欣赏图形的美,增强对数学的好奇心,激发学生的内在潜能.2011江苏卷与2012湖北卷两题的最后一问实际上就是变换了图形的位置,湖北卷将江苏卷中“过P作x轴的垂线”改为“过P作y轴的垂线”,其它条件完全一样,最后问题的设置也是相同的,处理的方法就是转化为斜率之积为-1,具体处理方法可见原高考参考答案,或可利用本文的推论1.2直接解出结果.
1.2 学会能将具体问题一般化 —— 力求推出一般性的结论,从而可以拓宽学生的视野,达到会一题而知一类的良好效果.
数学概念舍弃了具体形象的支撑而升华为抽象的文字,学生不易接受,但作为教者一定要有这样的能力和敏感直觉,对于2011江苏题如果我们再任意取一椭圆是否还有此完美的性质(垂直)呢?如果有那就太完美了,如果没有又会有什么规律可循呢?当然这就要求我们教师提前作一些准备.我们可以借助几何画板很轻松地得到一些数据,从而猜想并推导出结论,将之升华为一般性结论传授给学生,当然这中间过程的艰辛,也可让学生作一些参与,从而减轻学生的负担,大大提高了课堂的效率,激发了学生的学习潜能.2011江苏卷及2012湖北卷的最后一问实际上源于同一处理方法的两个结论,其结果是一个定值.(推导过程可参考文[1])
当然读者也可仿此将椭圆焦点放在y轴上推导出一般结论.通过对问题一般性结论的研究,不言而喻会对学生有很大的冲击力,从而对这一类问题有了本质的理解,而不是就题论题,搞题海战术.
王禹偁也继承了韩愈的观点,其《答张扶书》曰:“夫文,传道明心也,古圣人不得已而为之也”[注]曾枣庄、刘琳主编:《全宋文》第4册,《王禹偁·答张扶书》,成都:巴蜀书社,1989年,第357页。 ,强调文句必须“远师六经,近师吏部。使句之易道,义之易晓,又辅之以学,助之以气”[注]曾枣庄、刘琳主编:《全宋文》第4册,《王禹偁·答张扶书》,成都:巴蜀书社,1989年,第358页。 。又《三黜赋》曰:“屈于身兮不屈其道,任百谪而何亏? 吾当守正直兮佩仁义,期终身以行文。”[注]曾枣庄、刘琳主编:《全宋文》第4册,《王禹偁·三黜赋》,成都:巴蜀书社,1989年,第210页。
1.3 学会从圆、椭圆、双曲线、甚至抛物线之间找联系——类比可以使知识得以拓展,从而可以激发学生探索未知的欲望.
类比法在高中数学的许多方面都发挥着积极作用,它是人类获得新知识和解决问题的重要途径.美国数学家波利亚对类比法推崇倍至,他在《怎样解题》的第三部分谈到:“在我们的思维、日常谈话、一般结论以及艺术表演方法和最高科学成就中无不充满了类比.类比可在不同的水平使用……”“我们希望能预测结果,或者,至少在某种似乎可信的程度上预测结果的某些特征,这种似乎可信的预测通常是以类比为基础的.”
类比推理具有如下形式:A具有性质F1,F2,…,Fn,P;B具有性质F′1,F2′,…,Fn′,推测B具有性质P′,这里P′分别与F1,F2,…,Fn,P相同或相似,A和B指不同的对象或不同的事物.对题1、2我们也可将结论类比推广到双曲线:

当然读者也可仿此将双曲线焦点放在y轴上甚至可以将它类比到圆中推导出一般结论.
2 利用多媒体是产生新颖考题的又一新的领域——会用、善用、创新利用几何画板是我们的追求
几何画板是指专门用于数学“教”与“学”的计算机软件,在数学的教与学中有着重要的作用.代数公式的推导,图形与坐标的结合,函数规律的研究,统计与概率的模拟与仿真等,借助它可以很形象直观地帮我们了解甚至理解数学的本质.
2.1 利用几何画板可以帮我们寻找题目的根源——强化我们对问题本质的认识.


图①


图②
同时我们不免有这样的冲动,如果圆为定圆,变化椭圆得到的轨迹又会如何呢?(如图③)看似一双曲线部分图象,是否是双曲线呢?经过艰难的推导我们又会得到一个意外的收获.

图③
证明 设A(x1,y1),则B(x1,-y1),直线A1A的方程为

直线A2B的方程为

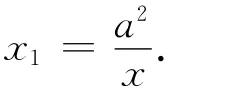

它告诉我们,几何画板虽然很形象,但也有迷惑性,结论还需我们加以验证与推导方可知其真伪.
2.2 利用几何画板可将自己的一些奇思妙想,甚至一个失误变成一个美妙的结论——培养我们的创新能力
由于本人的失误,误将圆与x轴的两个交点E、F分别当作点A1与A2,此时得到了如下图④的轨迹,其形如一双曲线的部分图象.这次又是否正确呢?经推导喜得:
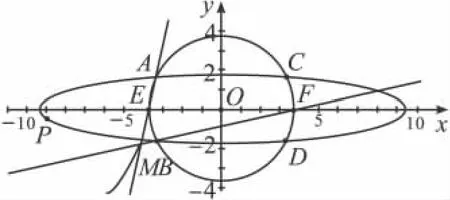
图④
以上仅为本人对近两年高考题中出现的解析几何题的一点思考,推导出来的一些结论也仅仅是茫茫解析几何中的一个小不点而已,特别是几何画板给我们带来的魅力及挑战,需要我们不断地学习.本文希望以此给读者带来教学和研究上的一点启示,仅此而已.
1 刘友明.一道试题多重价值[J].数学教学通讯,2011(7)

