平面几何定理的证明要注重培养学生的发散性思维

安徽省金寨一中 樊兴安 （邮编：237300）

发散性思维即求异思维，它具有多向性、灵活性、独特性等特点.要求在思考问题时多渠道、多角度、多方案，解题时要触类旁通、举一反三 .众所周知，古今中外，数学上很多伟大的发现来源于发散性思维，因而培养学生发散思维能力，对造就创造型人才至关重要.下面就利用平面几何中四边形内角和定理的多种证法，来培养学生的发散性思维，谈谈个人粗浅认识.

四边形内角和定理：四边形内角和为360°.

已知 ∠A、∠B、∠C、∠D是四边形ABCD的内角.

求证 ∠A＋∠B＋∠C＋∠D＝360°.

分析1 要引导学生善于运用转化的思想，用已知表示未知.由于三角形的内角和为180°，启发引导学生能否用三角形的内角和推出四边形的内角和？如何才能达到这个目的呢？为此要以三角形为依托，而图中无三角形，怎样才能达到这个目的呢？只有作辅助线.

证法1 如图1连结AC、BD并且交于O点.于是 ∠1＋∠10＋∠3＝180°，∠4＋∠5＋∠11＝180°，∠6＋∠7＋ ∠12 ＝ 180°，∠2＋∠8＋∠9＝180°.四个式子相加得 ∠BAD＋∠ABC＋∠BCD＋∠CDA＋∠9＋∠10＋∠11＋∠12＝720°.

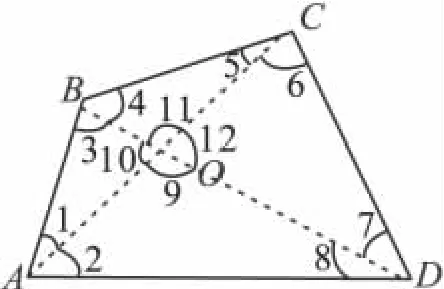
图1

∵∠9＋∠10＋∠11＋∠12＝360°，

∴∠BAD＋ ∠ABC＋ ∠BCD＋ ∠CDA＝360°.

分析2 证法1中的O为对角线的交点，O能否为四边形内除O以外的点呢？让学生们积极思考、动手作图，不难得出证法2.（如图2）

分析3 既然O在四边形内可行，

O是四边形的边上任一点是否可行？

学生们积极尝试，得到证法3.

证法3 （如图3）设O在AB边上，连结OC、OD，于 是 ∠A＋∠1＋∠7＝180°，

∠2＋∠3＋∠6＝180°，∠4＋ ∠5＋ ∠B＝180°三式相加得：

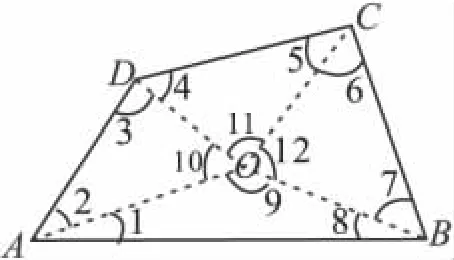
图2

∠A＋（∠1＋∠2）＋（∠3＋∠4）＋∠B＋∠5 ＋ ∠6 ＋ ∠7＝540°，

∵∠5＋∠6＋∠7＝180°，

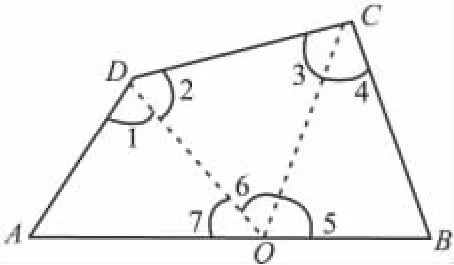
图3

∴∠A＋∠B＋∠BCD＋∠CDA＝360°.

分析4 既然O为四边形边上的任一点都能证明，那么O为AB边上的一个特殊点，比如DO／／BC（如图4）是否可行？是否还得像证法3那样连线呢？

证法4 设O在AB上且OD／／BC，则 ∠1＋∠3＋∠A＝180°，∠2＋∠C＝180°，两式相加得∠A＋∠3＋∠CDA＋∠C＝ 360°， 而 ∠3＝∠B，

图4

∴∠A＋∠B＋∠C＋∠CDA＝360°.

分析5O为证法4中的特殊点是否可行，比如说O为四边形的顶点是否可行？如何证明？

设O与B重合，连结OD（如图5）便得证法5，这即是教材中的证法.

分析6O可在四边形内部已得到证明，O也四边形的边上也已证明，

那么O在四边形外是否可以证明？如何证？

图5

图6

证法6 设O在四边形外，连结OA、OB、OC、OD则∠2＋∠1＋∠11＋ ∠10＝180°，∠3＋∠4＋∠9＝180°，∠5＋∠6＋∠7＋∠8＝180°.三式相加得（∠2＋∠3）＋（∠4＋∠5）＋∠6＋∠1＋∠7＋∠8＋∠9＋∠10＋∠11＝540°，而∠7＋∠8＋∠9＋∠10＋∠11＝180°，

∴∠DAB＋ ∠ABC＋ ∠BCD＋ ∠CDA＝360°.

以上分析，以O点的位置关系为主线，运用转化和分类讨论的数学思想，启发学生对O的位置展开讨论，充分发散了学生的思维，广泛开辟了解题途径，拓宽了解题思路，开阔了学生的知识视野，培养了学生的创新能力.