高中数学概念对解题思维形成的影响

安徽省铜陵市第一中学 李 晟 （邮编：233000）

什么是概念？概念是对客观事物的本质属性的概括和反映.只有当人们认识了事物的本质属性，才能给该事物一个恰当的名称，这个名称就是反映该事物本质属性的概念.因此，在解题过程中，数学概念的理解和运用往往对整个解题思维的形成有着支点的作用.下面就高中数学概念对解题思维形成的影响做一点浅显的探索.

1 概念的理解不透彻对解题思维的形成造成障碍

数学概念的理解对学生而言是难点.尤其是高中数学教学中的一些概念难点，往往在整个高中阶段的学习全部结束后有部分学生仍然是云里雾里，不知所云的.我们认为，概念的理解难点在于部分概念是全新的，是学生没有接触过的，因此在这部分概念的教学中就需要我们教师去着重的、详细的讲解.尤其是对每一个可能出现的理解歧义的地方作准确的、明确的解释.例如，在对函数y＝f（x）这个符号的理解上，很多学生到了高三都不清楚这个符号的具体含义，导致了在涉及到这个符号的解题过程中一错再错.在现行课本中明确的给出了y＝f（x）的解释：设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y＝f（x），x∈A.也就是说，y＝f（x）即“y是x的函数”的数学表示.然而对这个概念，很多学生在解决如下习题的时候还是产生了困惑.

例1 已知函数y＝f（2x＋1）的定义域是（1，5），求函数y＝f（x－3）的定义域.

常见的错误有：①因为1＜2x＋1＜5，所以0＜x＜2，所以－3＜x－3＜－1.

因此，函数y＝f（x－3）的定义域是（－3，－1）.

②因为1＜x＜5，所以3＜2x＋1＜11，所以0＜x－3＜8.

因此，函数y＝f（x－3）的定义域是（0，8）.等等.

其实，这些错误形成的本质原因是当y＝f（x）这个符号改变为y＝f（2x＋1）时，括号里面的式子的意义没有理解清楚.概念教学中我们经常对学生解释y＝f（x）中的x是函数的自变量，但并没有对x的另一身份给出明确的说法.如果我们做了如下解释：y＝f（2x＋1）是一个函数，这个函数的自变量是x，而2x＋1是法则f作用的对象.这样，对于符号y＝f（x）中的x的两重身份（x既是自变量，又是法则f作用的对象）学生就很清楚了.而这道例题就不至于产生解题思维上的混乱了.例题中法则f是同一个法则，所以f作用的对象的范围是一定的，即2x＋1和x－3的范围是一样的.解题过程如下：

因为1＜x＜5，所以3＜2x＋1＜11，所以3＜x－3＜11，所以6＜x＜14.

因此函数y＝f（x－3）的定义域是：（6，14）.

而形成这样清晰的认识后，对这一类y＝f（x）符号的理解问题在解题思维上就不会再产生理解错误了.例如若y＝f（x＋2）是奇函数，则我们得到的关系式是：f（－x＋2）＝－f（x＋2），而不是f（－x－2）＝－f（x＋2）.因为函数y＝f（x＋2）的自变量是x，而x＋2是法则f作用的对象.奇函数的定义式是f（－x）＝－f（x），这里x指的是自变量，也即函数的奇偶性是针对自变量而言的.

而有些概念在教学中应重点解释定义中的具体词句的意义.否则容易造成学生狭隘地理解概念，进而影响解题思维的形成.例如在概率中几何概型的定义是这样的：如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称几何概型.

而在这个定义中，对事件发生的概率计算何时使用面积比并没有很清晰的说明.大多数学生会对面积比形成一种很狭隘的理解，认为只有在已经形成的二维图形中才能使用面积比.实际上，几何概型中的事件发生的概率计算何时用长度比，何时用面积比应该是依据对事件发生时需要知道的变量个数来确定究竟是何种比值（即事件发生若只需要一个变量即可确定，则用长度比，若事件发生需要两个变量才可确定，则用面积比）.以下面这个习题为例，我们应该引导学生对定义中的词句做准确理解，进而应用到解题过程中去.

例2 如图，在已知四分之一圆AOB中，随机作两条射线OC和OD，与AOB交于C、D两点.则∠AOC＋∠BOD＜30°的概率是多少？

设 ∠AOC＝x，∠BOD＝y，则0＜x＜，0＜y＜，而事件∠AOC＋∠BOD＜30°则要求x＋y＜.

作出如右图形：

图中阴影部分面积占正方形面积的百分比即是事件∠AOC＋∠BOD＜30°的概率.

2 概念的灵活运用可以拓展思路，有助于解题思维的形成

对概念完全理解了，并不意味着学生就可以很好地运用概念来形成解题思路，进而拓展解题思维.高中阶段的很多比较巧妙的方法实际上是和定义戚戚相关的.数学家华罗庚说：“数学是一个原则，无数内容；一个方法，到处有用.”“善于退，足够地退，退到最原始而不失去重要性的地方，是学好数学的一个诀窍.”这段话我们把它用在定义概念的灵活使用上是再合适不过了.定义是数学的一个原则，也是数学解题的一种方法！退，退到定义和概念上来，解题往往有着意想不到的绝妙效果.

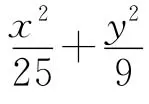
本题若是用方程来计算曲线间的相互关系将是非常复杂的.这里∠F1PF2的外角平分线的方程PN并不好计算，运算量会非常的大.而如果我们考虑使用椭圆的第一定义来解决这个求轨迹的问题，就非常简单了.

如图，将F2M延长交F1P的延长线于N点.

因为PM是∠F1PF2的外角平分线，而F2M⊥PM，

所以PF2＝PN，MN＝MF2.

由椭圆的第一定义可知：PF1＋PF2＝2a＝10，因此，有NF1＝PF1＋PN＝PF1＋PF2＝10.而OF＝OF，MN＝MF，故OM＝NF＝5，即1221点M的轨迹是以原点为圆心，半径为5的圆.

这种解法对学生的思维要求比较高，但平时如果训练得当的话，对学生的解题思维的拓展是非常有帮助的，既开阔了学生的解题视野，又培养了学生“巧解”难题的能力.

在高中圆锥曲线内容中，圆锥曲线的统一定义是解决一类过焦点的弦的相关问题的不二法门.通过统一定义的转化，往往可以把有关弦的计算问题转化为有关焦点和准线的平面几何问题，进而为求解寻求一种极为简单有效的方法.

我们再来看下面这个例子的几种解法.

解法1 设A（x1，y1），B（x2，y2）.

AB的方程为：y＝（x－c）.

联立双曲线方程得：

又b2＝c2－a2，代入 ④，得：e＝.

解法2 设A（x1，y1），B（x2，y2），AF＝ex1－a，BF＝ex2－a.

因为＝4，故ex1－a＝4（ex2－a），故3a＝4ex2－ex1①

因为kAB＝，故x1－x2＝｜AB｜，

故2（x1－x2）＝ex1＋ex2－2a②

①代入②，得：

6（x1－x2）＝3（ex1＋ex2）－2（4ex2－ex1）.

化简，得e＝.

解法3 如图，设直线AB交双曲线的右准线l于E，过A、B分别作AC⊥l于C，BD⊥l于D.

因为kAB＝，故 ∠E＝30°，AC＝AE，

第一种解法是最常见的，在解析几何中我们常常会把直线和圆锥曲线的很多位置关系转化为联立方程组以后的代数计算问题.几何上的相等关系（＝4）会转化为坐标的等量关系（y1＝－4y2），进而计算出需要的结果.但这种解法一般来说运算量比较大，稍不注意就会出错.第二种解法利用了双曲线的焦半径公式，计算量有所减小，但本质上和第一种解法是一样的，仍然属于用坐标代数运算去代替了几何中的图形之间的变换关系.而第三种解法是比较简便的一种算法.这里利用了双曲线的第二定义（即圆锥曲线的统一定义），把题目中所给的几何关系转化到了一组平行线中，利用比例线段很快地就得出了结果.比较上面的三种解法，我们发现第三种解法明显要简单一些，利用定义可以大大的简化运算.这就是定义的妙用了！

数学概念是严谨的，也是抽象的.它是数学这门学科的基石，正确地理解和形成一个数学概念，必须明确这个数学概念的内涵 —— 对象的“质”的特征，及其外延——对象的“量”的范围.一般来说，数学概念是运用定义的形式来揭露其本质特征的.所以我们在解题的过程中如果对概念的理解更加深刻一些，把握更加准确一些，运用更加灵活一些，那么就会把解题思维拓展得更宽，就会寻找到更好的简单有效的解题方法，就会让我们发现更多的数学乐趣！

1 邢素芳.数学概念浅谈［J］.内蒙古教育综合教育基础版，2010年（4）

2 张静.关于对高中数学解题思路的探索［J］.现代阅读（教育版），2012年（4）

3 童守军.应重视圆锥曲线定义的灵活应用［J］.中学数学，1994年（5）

4 范妍.重视数学概念建构，优化数学概念教学［J］.数学学习与研究 -教研版，2009年（7）

5 林承初.定积分概念的推广及其几何物理意义［J］.河南教育学院学报（自然科学版），2006年（2）