半群中的特殊模糊双理想的若干性质

张 磊，李世群

（湖南科技大学 数学与计算科学学院，湘潭411201）

0 引言及定义

1965年，美国控制论专家L.Zadeh教授引入了模糊子集的概念，随后Rosenfeld又引入了模糊子群和模糊子半群的概念，自此之后，其他学者在有关模糊代数方面的研究取得了相当丰硕的成果.模糊数学理论一个较大的发展是在1980年之后，这主要得益于模糊数学在应用领域的作为，特别是在日本的成功，日本学者Kuroki.N给出了半群的模糊理想、双理想等的概念［2］，并进行了研究，得到了关于半群模糊双理想的一些重要性质［1－4］.基于前人已有的成果，我们在本文中对这些结果进行了一定的推广，得到了关于半群的模糊双理想的若干性质.文献［2］给出了如下定义：

非空集合X到［0，1］的映射f称为X 的Fuzzy子集，且记X的全部Fuzzy子集所作成的集合为F（X），设f为给定集合的Fuzzy子集，对λ∈［0，1］，称fλ＝｛x｜f（x）≥λ｝为f的λ－截集.对于非空集合的X的任意子集A，定义集合A的特征函数为：fA：X→｛0，1｝，即

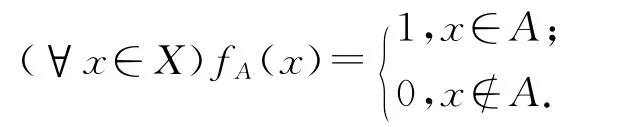
半群S的一个子半群B称为S的一个双理想，如果满足BSB⊆B，我们用B（S）表示半群S的所有双理想的集合，FB（S）表示半群S的所有Fuzzy双理想的集合.

半群S的一个双理想B称为半素的如果B满足条件

半群的所有半素双理想构成的集合记为SePB（S）；

LI－HE在文献［3］中给出了素双理想的定义：双理想B称为素的，如果B满足下列条件

∀C，D∈B（S） CD⊆B⇒（C⊆B）∨（D⊆B）.

文献［3］给出了刻画所有双理想为素的半群的结构的结论.

半群S的双理想B称为强素的，若B满足以下条件

半群S的双理想B称为强不可约的，若B满足以下条件

半群S称为正则的，如果对于任意的a∈S，存在x∈S，使得a＝axa［1］.

半群S称为内禀正则的，如果对于任意的a∈S，存在x，y∈S，使得a＝xa2y［1］.

半群S称为群半格若S是一族互不相交的子群Gi（i∈M，M 为脚标集）的并，满足对任意的i，j∈M，子群的乘积GiGj和GjGi包含于同一个Gk（k∈M）［1］.

Kuroki.N在文献［1，4－6］中给出了以下定义：

半群S的一个Fuzzy子集f称为S的一个Fuzzy子半群，若f满足条件

∀x，y∈S f（xy）≥min｛f（x），f（y）｝.

半群S的一个Fuzzy子半群f称为S的一个Fuzzy双理想，若f满足条件

∀x，y，z∈S f（xyz）≥min｛f（x），f（z）｝.下面的有关定义来自文献［2、7、9］.

对于半群S的Fuzzy子集f，g，f⊆g表示对任意的x∈S有f（x）≤g（x）.

半群的Fuzzy子集的乘积定义为

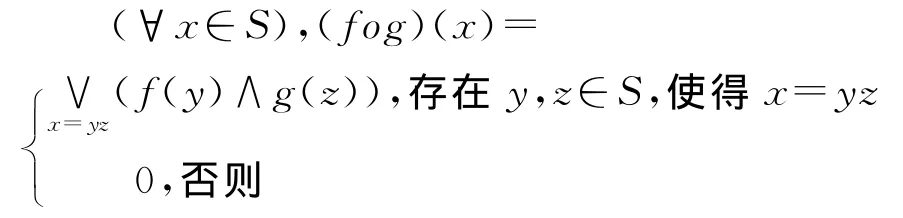
半群S的Fuzzy双理想P称为弱素的，若对A，B∈B（S），λ∈（0，1］，由λfAoλfB⊆P 推出λfA⊆P或λfB⊆P.

半群S的Fuzzy双理想f称为强不可约的，如果对S的任意Fuzzy双理想f1，f2若f1∩f2⊆f⇒f1⊆f或f2⊆f.

半群S的Fuzzy双理想f称为素的，如果对S的任意两个Fuzzy理想f1，f2若f1of2⊆f⇒f1⊆f或f2⊆f.

半群S的Fuzzy双理想f称为半素的，如果对S的任意Fuzzy双理想g，g2⊆f⇒g⊆f.

半群S的Fuzzy双理想f称为强素双理想，如果对S的任意Fuzzy双理想f1，f2.f1of2∩f2of1⊆f⇒f1⊆f或f2⊆f.

1 预备结论

Kuroki.N在文献［1］中给出了下列基本结论：

引理1设λ∈（0，1］，A，B为S 的任意子集，则

（1）A⊆B⇔λfA⊆λfB；

（2）λfAoλfB⊆λfAB；

（3）fA∩B＝fA∩fB.

引理2设S是半群，则下列各款等价：

（1）S 是群半格；

（2）对S的任意Fuzzy双理想g，h，goh＝g∩h.

引理3设f1，f2是S的任意两个Fuzzy双理想，则f1∩f2也是S的Fuzzy双理想.

引理4半群S正则且内禀正则当且仅当对于S的任意双理想f，有f2＝f.

而下面的引理5－8来自于文献［2］.

引理5设S为半群，P为S的Fuzzy双理想，则Pt（t＞0）是S的双理想，只要Pt≠Φ.

引理6设A为半群S的非空子集，fA为其特征函数，则A为S的双理想（理想，子半群）当且仅当fA为S的Fuzzy双理想（理想，子半群）.

引理7设f是S的任意Fuzzy双理想，g为S的任意Fuzzy子集，则fog和gof都是S的Fuzzy双理想.

引理8［3］设S 为任意半群，则SePB（S）＝B（S）当且仅当S为正则且内禀正则的.

2 主要结论

定理1半群S的双理想B是素的当且仅当其特征函数fB是Fuzzy弱素的.

证明：设B为S的素双理想，fB为其特征函数，B1，B2为S 的任意双理想，∀λ∈（0，1］，由于λfB1oλfB2⊆fB，λfB1oλfB2＝λfB1B2⊆fB，所以，∀x∈B1B2，

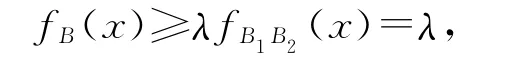
所以fB（x）＝1，推出x∈B，因此B1B2⊆B，由B为素双理想知B1⊆B 或B2⊆B，所以λfB1⊆fB1⊆fB或λfB2⊆fB2⊆fB，这说明fB为Fuzzy弱素的.

反之，设B为S的任意双理想，fB为其特征函数，且fB弱素，∀B1，B2∈B（S），若B1B2⊆B，由引理2.1，得fB1B2⊆fB，即fB1ofB1＝fB1B2⊆fB，由fB弱素知fB1⊆fB或fB2⊆fB，从而B1⊆B或B2⊆B，所以B为素的.

定理2半群S的所有双理想素当且仅当S的所有Fuzzy双理想都弱素.

证明：设P为S的任意Fuzzy双理想，∀λ∈（0，1］，λfB1oλfB2＝λfB1B2⊆P，我们有B1B2⊆Pλ，而Pλ为S的双理想，从而Pλ为S的素双理想，推出B1⊆Pλ或B2⊆Pλ，即λfB1⊆P，或λfB2⊆P，因此P为S的Fuzzy弱素双理想.

反之，设B为S 的任意双理想，且B1，B2∈B（S），B1B2⊆B，则fB1B2＝fB1ofB2⊆fB，由假设知fB弱素，所以fB1⊆fB或fB2⊆fB，所以B1⊆B或B2⊆B，所以B为素的，定理得证.

定理3在群半格中，Fuzzy双理想f为Fuzzy素双理想当且仅当f为强不可约的.

证明：设S为群半格，f为其Fuzzy双理想，若f为素双理想，∀g，h∈FB（S），若g∩h⊆f，由引理2有goh＝g∩h⊆f，所以有g⊆f或h⊆f，从而f是强不可约的.

反之，设f为强不可约的，∀g，h∈FB（S），若goh⊆f，

由引理2有g∩h＝goh⊆f，从而得g⊆f或h⊆f，所以f为素的.

定理4设A是S非空子集，fA为其特征函数，则若fA是S的强不可约Fuzzy双理想，那么A是S的强不可约双理想.

证明：设fA是S的强不可约Fuzzy双理想，由引理6知A是S的双理想，设B、C是S的双理想，且B∩C⊆A，则由引理1（3）有fB∩C＝fB∩fc⊆fA，从而由fA是S的强不可约Fuzzy双理想，所以fB⊆fA或fC⊆fA，由引理1（1）知B⊆A或C⊆A，从而A是S的强不可约双理想.

定理5半群S的每个强不可约半素Fuzzy双理想都是S的一个强素Fuzzy双理想.

证明：令f是半群S的一个强不可约半素Fuzzy双理想f1，f2∈FB（S），且f1of2∩f2of1⊆f，因为f1∩f2⊆f1，f1∩f2⊆f2，所以

（f1∩f2）2⊆f1of2∩f2of1⊆f，因为由引理3知f1∩f2是S的Fuzzy双理想，且f为Fuzzy半素的，推出f1∩f2⊆f，又f强不可约，所以f1⊆f或f2⊆f，所以f是强素的.

定理6在任意半群S中，下列各款等价：

（1）每个Fuzzy双理想幂等；

（2）f1of2∩f2of1＝f1∩f2，对任意f1，f2∈FB（S）；

（3）S的每个Fuzzy双理想f是半素的；

（4）S正则且内禀正则.

证明：（1）和（4）的等价性可直接由引理4推得.

（1）⇒（2）令f1，f2∈FB（S），则由引理3知f1∩f2∈FB（S），由假设知f1∩f2＝（f1∩f2）o（f1∩f2）⊆f1of2，同理可得f1∩f2⊆f2of1，所以f1∩f2⊆f1of2∩f2of1，由引理7知，f1of2和f2of1都是S的Fuzzy双理想，由引理3，f1of2∩f2of1也是S的Fuzzy双理想.由假设，有

f1of2∩f2of1＝（f1of2∩f2of1）2⊆（f1of2）o（f2of1）⊆f1oSoSof1⊆f1，

同理可得f1of2∩f2of1⊆f2，所以f1of2∩f2of1⊆f1∩f2.

综上所述，可得f1of2∩f2of1＝f1∩f2.

（2）⇒（1）令f是S的任意Fuzzy双理想，由假设我们有下式成立：

f＝f∩f＝fof∩fof＝fof，

所以S的任意双理想幂等.

（1）⇒（3）：令f 为S 的任意 Fuzzy双理想，∀f1∈FB（S），若f21⊆f，由（1）知f1＝f21⊆f，因此f为半素的.

（3）⇒（1）：对S的任意Fuzzy双理想f，由于f2是Fuzzy双理想，必有f2⊆f，又f2⊆f2且f2为Fuzzy半素双理想，推出f⊆f2，因此f＝f2.

（3）⇒（4）设B，C∈B（S）且C2⊆B，则由引理1（1）、（2）有fc2＝fcofc⊆fB，

由引理6知fB，fC均为S的Fuzzy双理想，由题设知fB是Fuzzy半素的，所以有

fC⊆fB，

由引理1（1）知有C⊆B，从而由定义知B是半素的，由B的任意性知S的任意双理想都是半素的，而半素双理想显然是双理想，所以有SePB（S）＝B（S），由引理8知S正则且内禀正则.

（4）⇒（3）设S为半群，满足正则且内禀正则的条件，f，g∈FB（S），且满足g2⊆f，对∀α∈S ，由S正则知∃x∈S，使得a＝axa，进一步有a＝axa＝ax（axa）＝axaxa，由S内禀正则知∃u，v∈S，使得a＝ua2v，所以有

所以对任意的a∈S，由已知条件及以上结果，有

g（a）≤g2（a）≤f（a），

所以有g⊆f，这就说明f是半素的.

由f选取的任意性知S的所有Fuzzy双理想都是Fuzzy素的.

定理7若半S的每个Fuzzy双理想幂等，则对S的任意Fuzzy双理想f，f强不可约当且仅当它强素.

证明：令f是S的强不可约Fuzzy双理想f1，f2∈FB（S），且f1of2∧f2of1⊆f，由定理6的（1）⇒（2）知，f1of2∧f2of1＝f1∧f2⊆f，但f是强不可约的，所以f1⊆f或f2⊆f，于是f为S 的强素的Fuzzy双理想.

反之，假设f是S的任意Fuzzy双理想，且∀f1，f2∈FB（S），f1∧f2⊆f，由定理6，我们有f1of2∧f2of1＝f1∧f2⊆f，但f强素，所以f1⊆f或f2⊆f，所以f是S的强不可约Fuzzy双理想.

［1］ Kuroki N .On Fuzzy Semigoups［J］.Inform .Sci，1991，53：203～236.

［2］ 谢祥云，吴明芬.半群的模糊理论［M］.北京：科学出版社，2005.

［3］ Shiqun Li，Yong He，On Semigroups Whose Bi－ideals Are Strongly Prime［J］.International Journal of Algebra，2007，1（6）：263－268.

［4］ Kuroki N.Fuzzy Generated Bi－ideals in Semigoups［J］.Inform .Sci，1992，66：235－243.

［5］ Kuroki N .On Fuzzy ideals and Fuzzy Bi－ideals in Semigoups［J］.FSS，1981，5：203－215.

［6］ Kuroki N .Fuzzy Bi－ideals in Semigoups［J］.Comment.Math.Univ.St.PAUL，1980，80：17－21.

［7］ 李世群，何 勇.所有双理想都是素双理想的半群［J］.数学学报（中文版），2006，49（5）：1189－1194.

［8］ Kehayopulu.N，Xie Xiang－yun，Tsingles.M.A Characterization of Prime and Semiprime Ideals of Semigroups in Terms of Fuzzy Subsets［J］.Soochow J.Math.，2001，27（2）：139－144.

［9］ A.Muhammad Rezvi，J.Mehmood.On Prime Fuzzy Bi－ideals in Ternary Semigroups［J］. МАТЕМАТИЧКИ ВЕСТНИК，2012，64（2）：79－96.