用于伺服驱动系统的无刷旋转变压器仿真设计

张晓宇

（江门职业技术学院 ，江门529090）

0 引 言

旋转变压器是一种把轴角信号转换成模拟信号的电磁感应式传感器，其以可靠性高、精度高、抗冲击、振动、以及能够提供高精度的位置信息等突出优点，广泛应用于要求可靠性高的各种伺服驱动控制系统中，但旋转变压器有电刷和滑环等接触结构，运转时有可能产生火花带来电磁干扰，而无刷旋转变压器没有电刷滑环的接触，具有无刷化、高可靠性、高精度、成本低廉和易于安装等优点，可以提高系统的可靠性和抗 冲击能力 ，适应条件恶劣的工作环境，并能连续高速，长寿命的运行.已被广泛应用于如航空、航天、雷达、坦克等军事装备，也用于数控机床和机器人等伺服驱动系统.

无刷旋转变压器是在接触式旋转变压器的基础上发展起来的，其结构形式很多，如环形变压器结构、电机铁心兼做环形变压器结构、转子杯结构等等.目前国内外采用比较多的是如图1所示的环形变压器结构，即用环形变压器来代替传统的电刷和滑环，以实现无接触.这种结构精度高，零位电压低，功率消耗小［1－4］.

本文详细地介绍了无刷旋转变压器的结构和工作原理，采用电磁场仿真软件Ansoft／Maxwell 2D设计，并进行瞬态磁场的仿真分析.通过仿真分析，得出了无刷旋变的两相输出电压和磁场分布图.分析了电机内磁场分布的规律，通过对参数进行优化设计，得到了符合要求的样机.

图1 无刷旋转变压器结构图

1 无刷旋转变压器工作原理

无接触旋转变压器具有一个或两个环形变压器，如图1所示，环形变压器的转子绕组与旋转变压器的转子绕组直接相连.当环形变压器的定子绕组施加励磁信号ER1R2＝Esinωt时，在环形变压器的转子绕组中就产生相应的感应电势，其大小与转子转角无关，此电势施加在旋转变压器的转子绕组上，即为旋转变压器的激磁电压，从而形成无刷结构，如图2所示［1］.

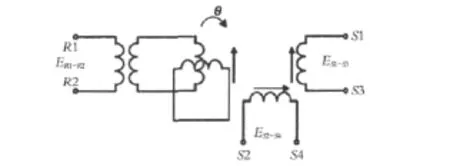
图2 无刷旋转变压器原理图

假定定、转子绕组匝数变比为k∶1，则两相正交绕组中将感应如下信号：

ES1S3＝UCOS＝kEsinωtcospθ

ES2S4＝USIN＝kEsinωtsinpθ

E——正弦波励磁电压幅值；

ω——正弦波励磁电压角频率；

k——电压比；

θ——转子角度；

p——极对数.

无接触旋转变压器励磁信号和两相输出信号波形如图3所示［2］.

图3 无刷旋转变压器励磁及输出波形

2 无刷旋变模型建立和磁场分析

2.1 模型建立

无刷旋转变压器由环形变压器及旋转变压器两部分组成，相关参数如表1所示.环形变压器结构相对简单，本文主要分析旋转变压器部分，采用电磁场仿真软件Ansoft／Maxwell 2D设计分析.

首先应用Maxwell 2D，建立二维有限元模型，然后再进行磁场分析 ，并计算气隙磁密 ，在此基础上求解输出波形.Maxwell是Ansoft公司的电磁场有限元分析软件 ，它的高性能矩阵求解器、多CPU处理能力、自适应的网格剖分技术和用户定义材料库等特点 ，使其可以快速完成磁场分析.

表1 样机设计参数

旋转变压器二维有限元模型如图4所示.

图4 旋转变压器二维有限元模型

2.2 材料特性及激励源设置

在指定材料属性时，定、转子冲片所采用的硅钢片材料的型号是DW310，导线材料设置为铜（copper），气隙和转动带都设置为真空（vacuum）.在Ansoft／maxwell 2D的材料数据库中并没有该种材料，所以要将B－H曲线离散化再将其中的值输人到材料赋值器中自定义该种材料拟合出材料的B－H曲线.

二维瞬态分析中可以设置的激励源有：实体电流、实体电压、表面电流以及外部电路，本文分析的无接触旋转变压器为单相励磁，两相输出，因此选用单相交流电压激励，u＝ 7sin2000πt.

2.3 有限元网格剖分

有限元法是以变分原理和近似插值离散为基础的一种数值计算方法，它的计算精度取决于剖分单元的大小与单元的分布 一般来说，单元数越多，则近似解的精度就越高，为了得到较精确的计算结果，单元的大小与单元的疏密分布要合理，合理的网格需要在网格自动剖分程序所生成的初步网格基础上，由网格细分环节来得到，气隙是最重要的部分，对其进行手动剖分.有限元剖分图如图5所示.

图5 旋转变压器网格剖分图

2.4 后处理

对模型分别用magnetostatic及transient模块设置并求解，通过Ansoft／maxwell 2D软件强大的后处理功能，可得到相应参数的仿真结果，用以分析判断无刷旋变性能是否达到所需的要求，若不满足，可以调整相应的参数，重新建模仿真.

2.5 有限元分析结果

通过对模型的有限元仿真分析，可以得到无刷旋变空载磁密及磁力线分布，如图6、图7所示.对其两相输出绕组分别按正弦绕组设置，仿真分析可得到两相正余弦输出绕组玻形，如图8所示.

图8 旋转变压器正余弦输出波形图

3 结 语

本文简要分析了无刷旋转变压器中关键的旋转变压器部分的仿真设计，利用电磁场仿真软件Ansoft／Maxwell 2D的 magnetostatic及transient模块建立有限元仿真模型并求解得到旋转变压器的磁场分布及输出电压波形，通过对其气隙大小及绕组匝数的优化设计，得到了满足要求的优化方案，为以后快速、准确设计无接触旋转变压器打下基础.

［1］ J o a～o Figueiredo.Resolver Models for Manu Facturing［J］.IEEE Transactions on Magnetics，2011，58 （8）：3693－3670.

［2］ Ruijie Zhao，Xuejun Tao，etal.Research on The Decoding Method of Resolver［J］.IEEE Transactions on Magnetics，2011，11（1）：329－333.

［3］ Lazhar Ben－Brahim，Mohieddine Benammar，etal.A New Angle Determination Method For Resolvers［J］.IEEE Transactions on Magnetics，2008，08（2）：126－131.

［4］ H.S.Mok，S.H.KimandY.H.Cho.Reduction of PMSM Torque Ripple Caused by Resolver Position Error［J］.IEEE Transactions on Magnetics，2007，42（11）：121－125.