m-半格矩阵的M-P广义逆

赵 娜

(长治医学院 数学教研室,山西 长治 046000)

广义逆矩阵是矩阵论的重要分支,在数理统计、优化计算、图像处理、控制论等众多领域有广泛应用[1]．m-半格把∨-半格的结构与半群的乘法运算结合起来,从而剩余格,Frame,Quantale,格序半群等都是特殊的m-半格[2]．关于一些非交换代数如体、环、坡、Quantale等代数结构上矩阵的广义逆已有一些研究[3-10],本文受此启发,给出了m-半格矩阵M-P广义逆的定义,得到了m-半格矩阵存在M-P广义逆的一些等价刻画和显示表达式．

1 预备知识

定义1 设(Q,∨)是一个半格,*是Q上的二元运算．若Q满足:

(i)∀a,b,c∈Q,有(a*b)*c=a*(b*c);

(ii)∀a∈Q,a*_和_*a都保有限并;

则称(Q，∨)是m-半格,简称Q是m-半格．用0,1分别表示Q中的最小元、最大元．这里的定义比文献[2]定义的m-半格更一般化．

定义2 设Q是m-半格,如果∀a,b∈Q,有a*b=b*a,则称Q是交换m-半格．

定义3 设Q是m-半格,e∈Q,泉若∀x∈Q,e*x=x*e=x,则称e是Q的单位元;若Q有单位元1,则称Q为单位m-半格．

如果不加特殊说明,以下文中给出的m-半格都是单位交换m-半格．为了方便,∀a,b∈Q,记ab=a*b,a+b=a∨b．

Mm×n(Q)(m,n∈N+)表示m-半格Q上所有m×n矩阵构成的集合,aij表示m-半格矩阵A的第i行第j列元素．如果m=n,则将Mm×n(Q)记为Mn(Q)．

对于任意A=(aij),B=(bij),C=(cij)∈Mm×n(Q),D=(dij)∈Mn×m(Q),定义:

A≤B⟺aij≤bij;C=A+B⟺cij=aij+bij;C=aB⟺cij=abij;A=B⟺aij=bij;D=AT⟺dij=aji;

对于任意A=(aij)∈Mm×k(Q),B=(bij)∈Mk×n(Q),C=(cij)∈Mn×m(Q),E∈Mn(Q),

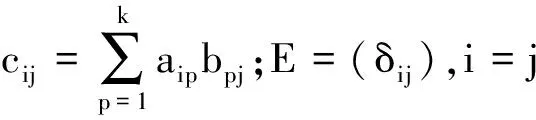
性质1m-半格矩阵满足以下运算律:

(i)A+A=A;(ii)AE=EA=A;(iii)(AB)C=A(BC);(iv)A(B+C)=AB+AC;(A+B)C=AC+BC;(v)(AB)T=BTAT;

推论1Mm×n(Q)是一个单位非交换m-半格．

定义4 设Q是m-半格,A,E∈Mn(Q),如果存在m-半格矩阵B∈Mn(Q),使得AB=BA=E,则称A为可逆的,B为A的逆,记为A-1．若A可逆,A-1=AT唯一,(A-1)-1=A．

定义5 设Q是m-半格,A∈Mm×n(Q),如果AGA=A,则称G∈Mn×m(Q)为A的广义逆,记为A-．若A可逆,A-=A-1．一般地,A-不唯一,(A-)-≠A．

引理设Q是m-半格,A,B∈Mm×n(Q),若∀b∈Mn×1(Q),Ab=Bb,则A=B．

定理1 设Q是m-半格,A∈Mm×n(Q),则G∈Mn×m(Q)是A的广义逆的充分必要条件是对于∀b∈Mm×1(Q),若方程AX=b有解,则Gb必是其解．

引理、定理1是文献[4]中引理2.1、定理2.1的推广,证明过程类似．

2 m-半格矩阵的M-P逆

定义6 设Q是m-半格,A∈Mm×n(Q),如果存在G∈Mn×m(Q),满足AGA=A,GAG=G,(AG)T=AG,(GA)T=GA,则称A是M-P可逆的,G为A的M-P广义逆或伪逆,记为A+．

显然,A的M-P广义逆A+是A的广义逆．当A可逆时,A+=A-1．

性质2 设Q是m-半格,A∈Mm×n(Q)存在M-P广义逆A+,则

(i)(A+)+=A;

(ii)(AT)+=(A+)T;

(iii)A+唯一.

证明 (i)(ii)由定义中条件的对称性直接可得．

(iii)设X,Y均为A的M-P广义逆,

AXA=A⟹AXAY=AY,AY=(AY)T=(AXAY)T=(AY)T(AX)T=AYAX=AX,

同理YA=XA．

AY=AX⟹YAY=YAX=XAX⟹Y=X．

定理2 设Q是m-半格,A∈Mm×n(Q?,则A是M-P可逆的充分必要条件是AAT,ATA可逆．

证明 必要性 设G是A的M-P广义逆,∀b∈Mn×1(Q),AATGTGb=A(GA)TGb=AGAGb=AGb,由定理1知,AATGTGb=b,由引理得,AATGTG=E,同理GTGAAT=E,即AAT可逆,(AAT)-1=GTG．

同理可证ATA可逆,(ATA)-1=GGT．

充分性设AAT,ATA可逆,令G=ATAAT=AT(AAT)-1=(ATA)-1AT,满足M-P广义逆的定义．

此定理一定程度上表明了M-P可逆与可逆之间的关系,m-半格矩阵的M-P广义逆是m-半格方阵的逆的一般化．

推论2 (i)若A是M-P可逆的,则A+=ATAAT;

(ii)AA+=Em,A+A=En;

(iii)(AB)+=B+A+,特别地,(ATA)+=A+(AT)+.

定理3是文献[9]定理3.3的推广,证明过程类似．特别地,(A+B)+=A++B+．由性质2(i),推论2(iii)知,M-P广义逆在定理3条件下是Mm×n(Q)上的对合运算,Mm×n(Q)是对合m-半格．

定理4 设Q是m-半格,A∈Mm×n(Q),则A是M-P可逆的充分必要条件是存在G∈Mn×m(Q)使得GAAT=AT,AGGT=GT．

证明 充分性GAAT=AT⟹GAATGT=ATGT⟹GA(GA)T=(GA)T⟹GA(GA)T=GA⟹GAATGT=GA⟹ATGT=GA⟹(GA)T=GA,代回GAAT=AT得(GA)TAT=AT⟹AGA=A．由对称性可证AGGT=GT⟹(AG)T=AG,GAG=G．

必要性AGA=A,(GA)T=GA⟹A(GA)T=A⟹GAAT=AT．由对称性可证GAG=G,(AG)T=AG⟹AGGT=GT．

定理5 设Q是m-半格,A∈Mm×n(Q),则G∈Mn×m(Q)是A的M-P广义逆的充分必要条件是∀b∈Mm×1(Q),若方程AX=b有解,则Gb是唯一解．

证明 必要性 设G是A的M-P广义逆,则G是A的广义逆,由定理1知,若方程AX=b有解,则Gb是解．设Z也是AX=b的解,则Gb=ATAATb=(ATA)-1ATAZ=Z．

充分性 假设G不是A的M-P广义逆,∀b∈Mm×1(Q),AA+b=AAT(AAT)-1b=b,A+b是AX=b的解,与Gb是唯一解矛盾,故G是A的M-P广义逆．

定义7 设Q是m-半格,A∈Mn(Q),如果存在m-半格矩阵X∈Mn(Q),满足AkXA=Ak,XAX=X,AX=XA,则称X为A的Drazin逆,记为AD．若A是Drazin可逆的,AD唯一．若A可逆,AD=A-1．特别地,当k=1时,称X为A的群逆,记为A#．

定理6 设Q是m-半格,A∈Mm×n(Q),则A是M-P可逆的充分必要条件是AAT群逆存在且方程A=AATX有解．

证明 充分性 若AAT的群逆(AAT)#存在且方程A=AATX有解,令B=(AAT)#A,则

BATA=(AAT)#AATA=AAT(AAT)#A=AAT(AAT)#AATX=AATX=A;(ABT)T=(BATABT)T=BATABT=ABT;(XTA)T=(XTAATX)T=XTAATX=XTA;令G=XTABT,则AGA=AXTABTA=AATXBTA=ABTA=BATA=A;GAG=XTABTAXTABT=XTBATAATXBT=XTAATXBT=XTABT=G;AG=AXTABT=AATXBT=ABT⟹(AG)T=AG;GA=XTABTA=XTBATA=XTA⟹(GA)T=GA,即G是A的M-P广义逆矩阵．

必要性 若G是A的M-P广义逆,则AG=Em,GA=En．令Y=GTG,则AATYAAT=AATGTGAAT=AAT;YAATY=GTGAATGTG=GTG=Y;AATY=AATGTG=E=GTGAAT=YAAT,即Y是AAT的群逆．

AATGT=A(GA)T=A,即GT是方程A=AATX的解．

定理6′ 设Q是m-半格,A∈Mm×n(Q),则A是M-P可逆的充分必要条件是ATA群逆存在且方程A=XATA有解．

定理7 设Q是m-半格,A∈Mm×n(Q),则A是M-P可逆的充分必要条件是方程组AATX=A,XATA=A有解．

证明 必要性 由定理6,6′知(A+)T是方程组的解．

充分性 设方程组AATX=A,XATA=A的解为G,AGTA=AGT(AATG)=A(GTAAT)G=AATG=A,下证GTAGT是A的M-P广义逆．

A(GTAGT)A=(AGTA)GTA=AGTA=A;(GTAGT)A(GTAGT)=GT(AGTA)GTAGT=GTAGTAGT=GT(AGTA)GT=GTAGT;

[A(GTAGT)]T=(GTAGT)TAT=GATGAT=GAT=GATAGT=AGT=(GAT)T=(GATGAT)T=A(GTAGT);

[(GTAGT)A]T=AT(GTAGT)T=ATGATG=ATG=GTAATG=GTA=(ATG)T=(ATGATG)T=(GTAGT)A．

定理8 设Q是m-半格,A∈Mm×n(Q),则下列条件等价:

(i)A是M-P可逆的;

(ii)AT是M-P可逆的;

(iii)AAT,ATA可逆;

(iv)存在G∈Mn×m(Q),使得AG=Em,GA=En;

(v)存在G∈Mn×m(Q),使得GAAT=AT,AGGT=GT;

(vi)(AAT)#存在,且方程A=AATX有解;

(vii)(ATA)#存在,且方程A=XATA有解;

(viii)方程组AATX=A,XATA=A有解;

(ix)∀b∈Mm×1(Q),若方程AX=b有解,则A+b是唯一解.

定义8 设Q是m-半格,A∈Mm×n(Q),A的第i行(列)与第j行(列)是正交的,如果对∀l,k∈N+,当k≠l,总有aikajl=0(akialj=0)．特别地,当i=j时,则称第i行(列)是正交的．

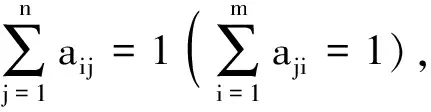
定理9 设Q是m-半格,A∈Mm×n(Q),AT是A的M-P广义逆矩阵的充分必要条件是A每行每列都是1的分解且都是正交的．

证明 设A=(aij)∈Mm×n(Q),则

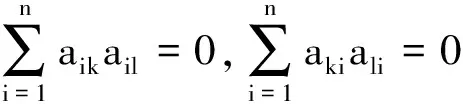
即A每行每列都是1的分解且都是正交的⟺AAT=Em,ATA=En⟺A+=AT．

推论3A∈Mn(Q),A-1=AT⟺A每行每列都是1的分解且都是正交的．