m-半格的粗糙模糊理想
周 欣,赵 彬
(陕西师范大学 数学与信息科学学院,西安 710062)
m-半格的粗糙模糊理想
周 欣,赵 彬
(陕西师范大学 数学与信息科学学院,西安 710062)
应用粗糙集理论给出m-半格上由模糊(素)理想诱导的同余及关于这种同余上(下)粗糙模糊近似算子的性质.通过引入m-半格粗糙模糊(素)理想的概念,讨论了m-半格上粗糙模糊(素)理想与模糊(素)理想的关系及粗糙模糊(素)理想与(素)理想的关系.
m-半格;上(下)粗糙模糊近似算子;(模糊)理想;粗糙模糊(素)理想
粗糙集理论[1]在人工智能、数据分析和认知科学中应用广泛.文献[2-3]给出了粗糙集的代数性质.自Biswas等[4]引入粗子群的概念以来,许多学者将粗糙集理论的研究方法应用到多种代数结构[5-7]和格结构[8-11]中.Estaji等[12]在格上研究了模糊子集上、下近似集的性质;文献[13-14]分别研究了可换环与半群上的粗糙素理想及粗糙模糊素理想的结构.上述研究方法也可用于m-半格的研究中.m-半格将∨-半格结构与半群的乘法运算相结合,是剩余格、Frame、Quantale和格序半群的推广.含最大元的m-半格上所有∨-半格理想组成的集合是一个Quantale,并且每个凝聚式Quantale都同构于某个含最大元的m-半格上所有∨-半格理想组成的集合[15].理想是刻画代数结构的重要工具.本文通过引入m-半格的粗糙模糊理想的概念,讨论m-半格的粗糙模糊(素)理想与模糊(素)理想的关系,给出了上(下)粗糙模糊理想和理想的等价刻画,并探讨了m-半格的上、下粗糙模糊理想之集的序性质.
1 预备知识
定义1设(S,∨)是∨-半格,·是S上的乘法运算,且满足:
1)∀a,b,c∈S,(a·b)·c=a·(b·c);
2)∀a∈S,a·_和_·a都保有限并.
则称(S,∨,·)是m-半格,简称S是m-半格.
由m-半格的定义知(S,·)是半群.定义1是文献[15]中m-半格定义的推广.
设S是m-半格.若∀a,b∈S,a·b≤a且a·b≤b,则称S是负序m-半格.对偶地,可以给出正序m-半格的定义.显然,若将格中∨视为乘法运算,则格是正序m-半格.本文若无特别说明,S均指m-半格.为简便,用ab标记a·b(a,b∈S).
设S和T是两个m-半格,且φ:S→T是一个映射.若∀a,b∈S,φ(a∨b)=φ(a)∨φ(b),且φ(ab)=φ(a)φ(b),则称φ是m-半格同态.若φ是满射,则称φ是满的m-半格同态.若φ是单射,则称φ是单的m-半格同态.若φ是双射,则称φ是m-半格同构.
设θ是S上的等价关系.如果θ与S的∨和·相容,即∀(a,b),(c,d)∈θ⟹(a∨c,b∨d),(ac,bd)∈θ,则称θ是S上的m-半格同余,简称θ是S的同余.用[a]θ表示a的θ-同余类,用Con(S)表示S上的同余之集,则(Con(S),⊆)是一个完备格.
定义2设θ是S上的同余,若∀a,b∈S,[a∨b]θ={x∨y:x∈[a]θ,y∈[b]θ},则称θ是∨-完备的.类似地,如果∀a,b∈S,[ab]θ={xy:x∈[a]θ,y∈[b]θ},则称θ是·-完备的.若同余θ既是∨-完备的又是·-完备的,则称θ是完备同余.
定义3设S是m-半格且I⊆S,若I满足下列条件1)和2),则称I是S的∨-半格理想;若I满足下列条件1)~3),则称I是S的m-半格理想,简称I是S的理想:
1)∀a,b∈S,a,b∈I⟹a∨b∈I;
2)∀a,b∈S,b≤a∈I⟹b∈I;
3)∀a,b∈S,b∈I⟹ab∈I且ba∈I.


设S是m-半格且f,g∈F(S).定义f∘g为:

运算“∘”满足结合律[17],由文献[18]引理2.1知,若f,g,h∈F(S)且f⊆g,则f∘h⊆g∘h且h∘f⊆h∘g.
设A⊆S,χA是A的特征函数且λ∈[0,1].定义S的模糊子集λχA为:∀x∈X,




命题1设θ是m-半格S上的等价关系,f∈F(S),则∀t∈[0,1],有:

命题2设θ是m-半格S上的等价关系,则∀f,g∈F(S)及∀{fi}i∈I⊆F(S),有:





2 上(下)粗糙模糊近似算子
定义5设S是m-半格,f∈F(S),若f满足下列条件:
1)∀x,y∈S,f(x)∧f(y)≤f(x∨y);
2)∀x,y∈S,x≤y⟹f(y)≤f(x);
3)∀x,y∈S,f(x)≤f(xy)∧f(yx).
则称f为S的模糊m-半格理想,简称f为S的模糊理想.
设f是S的非常值模糊理想.若∀x,y∈S,f(xy)=f(x)∨f(y),则称f是S的模糊素理想.
注11)定义5中的条件1)和2)可用条件∀x,y∈S,f(x∨y)=f(x)∧f(y)等价替换,并且3)可用∀x,y∈S,f(x)∨f(y)≤f(xy)等价替换;
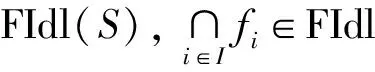


图1 S上的乘法运算Fig.1 Multiplication of S


设S是m-半格,f∈F(S)且1∈Imf,定义

其中Imf表示f的像集.
引理1设S是m-半格,f,g∈F(S),1∈Imf∩Img,则:






且

设θ1和θ2是m-半格S上的两个二元关系,则θ1和θ2的复合θ1∘θ2定义为
θ1∘θ2={(x,y)∈S×S:∃z∈S,使得(x,z)∈θ1且(z,y)∈θ2}.
命题4若S是正序m-半格,且f∈FIdl(S),则f是常值映射.
证明:设x,y∈S.因为S是正序的,所以x∨y≤xy.由f∈FIdl(S)知
f(x∨y)=f(x)∧f(y)≤f(x)≤f(xy)≤f(x∨y),
故f(x∨y)=f(x).同理可证f(x∨y)=f(y).因此,f(x)=f(y).
命题5[19]设S是m-半格.若f,g∈FIdl(S),则f∘g∈FIdl(S).特别地,若f,g∈FIdl(S)*,则f∘g∈FIdl(S)*.
定理1设S是m-半格,f,g∈F(S),1∈Imf∩Img,则下列结论成立:





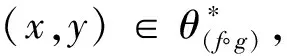


2)显然成立.
a∨m′∨n′=m∨m′∨n′=x∨m′∨n′,


从而

故

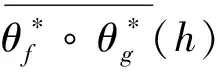

(x∧bc)∨(x∧b′c)=x∧(bc∨b′c)=x∧(yc∨b′c)=(x∧yc)∨(x∧b′c),
且


因此,



即

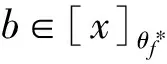

因此,
所以


证明:设S为一个格,θ为S上的格同余,且x,y,z∈S.若x≤yz,b∈[y]θ且c∈[z]θ,则(bc,yz)∈θ,从而(x∧bc,x)=(x∧bc,x∧yz)∈θ,即x∧bc∈[x]θ.由x∧bc≤bc知,

3 粗糙模糊(素)理想

本文给出的m-半格理想和模糊理想分别与文献[20]和文献[21]给出的Quantale理想和模糊理想的定义形式相同,所以类似地有下列结论.
引理2设θ是m-半格S上的同余,I是S的理想,则下列结论成立:





引理3[19]设S是m-半格,f是S的模糊子集,则下列结论成立:
1)f是S的模糊理想当且仅当∀t∈[0,1]∩,ft是S的理想;
2)f是S的模糊理想当且仅当∀t∈[0,1]∩,是S的理想;
3)若f是S非常值的模糊子集,则f是S的模糊素理想当且仅当∀t∈[0,1]∩,若ft≠S,ft是S的素理想;
4)若f是S非常值的模糊子集,则f是S的模糊素理想当且仅当∀t∈[0,1]∩,若
命题7设θ是m-半格S上的等价关系,f是S的模糊子集,则下列结论成立:
1)f是S关于θ的上粗糙模糊理想当且仅当∀t∈[0,1]∩,是S的理想;
2)f是S关于θ的下粗糙模糊理想当且仅当∀t∈[0,1]∩,是S的理想;
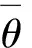

命题8设θ是m-半格S上的∨-完备同余,f是S的模糊理想,则下列结论成立:
1)f是S关于θ的上粗糙模糊理想;
2)若S是负序的,则f是S关于θ的下粗糙模糊理想;
3)若θ是完备同余,则f是S关于θ的下粗糙模糊理想.
证明:1)设t∈[0,1]∩,则由引理3知是S的理想,从而由命题1和引理2可得是S的理想.故由引理3知是S的模糊理想.
同理可证2)和3).
命题9设θ是m-半格S上的完备同余,f是S的模糊素理想,则下列结论成立:


推论1设θ是m-半格S上的∨-完备同余,f是S的模糊理想.若S是负序的或θ是完备同余,则f是S关于θ的粗糙模糊理想.

命题8和命题9表明,在某些条件下,上、下粗糙模糊(素)理想是m-半格的模糊(素)理想的推广.下面举例说明命题8中2),3)的逆命题一般不成立.


2)设S是如图2(A)所示的∨-半格,令S上的乘法运算·=∨,则(S,·,∨)是m-半格.设θ是1)中给出的等价关系,则θ是S上的完备同余.若取f为1)中给出的模糊子集,则易见f是关于θ的下粗糙模糊理想,但不是S的模糊理想.
下面举例说明若没有条件“θ是完备同余”,则命题9的结论可能不成立.
例3设S是如图2(B)所示的格,令S上的乘法运算·=∧,则易验证(S,·,∨)是m-半格.
设θ是S上的等价关系,并且θ的等价类为:

显然θ是S上的同余.因为

(1)
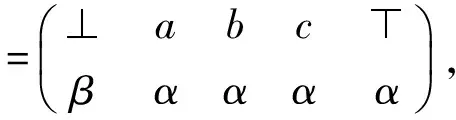


例4设S是如图2(C)所示的格,令S上的乘法运算·=∧,则易验证(S,·,∨)是m-半格.
设θ是S上的等价关系,并且θ的等价类为:

易见θ是S上的同余.因为式(1)成立,且

所以θ既不是∨-完备的也不是·-完备的.因此,θ不是完备同余.定义模糊子集f为

则

易证f是S的模糊素理想.因为



图2 S的Hasse图Fig.2 Hasse graph of S
引理4设S是负序m-半格且满足∀a∈S,a2=a,f是S的模糊素理想.定义S上的关系θf为
(x,y)∈θf⟺f(x)=f(y)=0或f(x)和f(y)都不为0,
则θf是S上的完备同余.
定理2设S是负序m-半格且满足∀a∈S,a2=a,f是S的模糊素理想.若g是S的模糊理想,则g是S的关于θf的粗糙模糊素理想.
证明:由引理4知θf是S的完备同余.设x,y∈S.因为
且


由
知,

类似地,也可证若f(xy)=f(y),则


引理5设A是m-半格S的子集,且θ是S上的等价关系,则∀x∈S,有:



命题10设A是m-半格S的子集,θ是S上的等价关系,则:



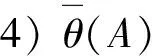
推论3设A是m-半格S的子集,θ是S上的等价关系,则:


引理6设S和S′是两个m-半格,φ:S→S′是一个满的m-半格同态,θ′是S′上的同余.令θ={(x,y)∈S×S:(φ(x),φ(y))∈θ′},则∀A⊆S,有:
1)θ是S上的同余;





证明:可参考文献[20]中命题6.3、引理6.5和定理6.6的证明.
设S和S′是两个m-半格,φ:S→S′是一个映射,且f∈F(S).定义模糊子集φ(f)为:∀y∈S′,φ(f)(y)=∨{f(x):φ(x)=y,x∈S}.φ(f)称为模糊子集f在映射φ下的标准Zadeh像[22].易见若φ是双射,则φ(f)(x′)=f(x),其中φ-1(x′)=x.
命题11设S和S′是两个m-半格,φ:S→S′是一个满的m-半格同态,θ′是S′上的同余.若θ是引理6给出的S上的同余,则∀f∈F(S),有:


证明:易验证∀t∈[0,1]∩及∀f∈F(S)都成立:① (φ(f)且Ø⟺Ø;② 若φ是m-半格同构,则(φ(f))t=φ(ft),且Ø⟺Ø.

2)证明过程与1)类似.
推论4设S和S′是两个m-半格,φ:S→S′是m-半格同构,θ′是S′上的同余.若θ是引理6中S上的同余,则∀f∈F(S),f是S关于θ的粗糙模糊(素)理想当且仅当φ(f)是S′关于θ′的粗糙模糊(素)理想.


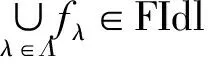
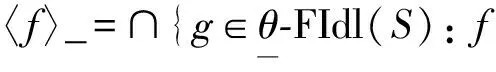




所以∪{〈fA〉_:A是S有限子集}⊆f.设x∈S,取B={x},则
f(x)=fB(x)≤〈fB〉_(x)≤(∪{〈fA〉_:A是S有限子集})(x).
从而f⊆∪{〈fA〉_:A是S有限子集}.因此,
f=∪{〈fA〉_:A是S有限子集}.
[1] Pawlak Z.Rough Sets [J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[2] Järvinen J.Lattice Theory for Rough Sets [C]//Transactions on Rough Sets Ⅳ.Berlin:Springer,2007:400-498.
[3] LIU Guilong,ZHU William.The Algebraic Structures of Generalized Rough Set Theory [J].Information Sciences,2008,178(21):4105-4113.
[4] Biswas R,Nanda S.Rough Groups and Rough Subgroups [J].Bulletin of the Polish Academy of Sciences Mathematics,1994,42(3):251-254.
[5] Dawaz B.Roughness in Rings [J].Information Sciences,2004,164(1/2/3/4):147-163.
[6] Kuroki N.Rough Ideals in Semigroups [J].Information Sciences,1997,100(1/2/3/4):139-163.
[7] Dubois D,Prade H.Editorial [J].Fuzzy Sets and Systems,1987,24(3):259-262.
[8] CHEN Degang,ZHANG Wenxiu,Yeung D,et al.Rough Approximations on a Complete Completely Distributive Lattice with Applications to Generalized Rough Sets [J].Information Sciences,2006,176(13):1829-1848.
[9] Estaji A A,Hooshmandasl M R,Davvaz B.Rough Set Theory Applied to Lattice Theory [J].Information Sciences,2012,200:108-122.
[10] LIU Guilong.Generalized Rough Sets over Fuzzy Lattices [J].Information Sciences,2008,178(6):1651-1662.
[11] QI Guilin,LIU Weiru.Rough Operations on Boolean Algebras [J].Information Sciences,2005,173(1/2/3):49-63.
[12] Estaji A A,Khodaii S,Bahrami S.On Rough Set and Fuzzy Sublattice [J].Information Sciences,2011,181(18):3981-3994.
[13] Kazanci O,Dawaz B.On the Structure of Rough Prime (Primary)Ideals and Rough Fuzzy Prime (Primary)Ideals in Commutative Rings [J].Information Sciences,2008,178(5):1343-1354.
[14] XIAO Qimei,ZHANG Zhenliang.Rough Prime Ideals and Rough Fuzzy Prime Ideals in Semigroups [J].Information Sciences,2006,176(6):725-733.
[15] Rosenthal K I.Quantales and Their Applications [M].New York:Longman Scientific and Technical,1990.
[16] Zadeh L A.Fuzzy Sets [J].Information and Control,1965,8:338-353.
[17] Kehayopulu N,Tsingelis M.The Embedding of an Ordered Groupoid into a Poe-Groupoid in Terms of Fuzzy Sets [J].Information Sciences,2003,152:231-236.
[18] XIE Xiangyun,TANG Jian.Fuzzy Radicals and Prime Fuzzy Ideals of Ordered Semigroups [J].Information Sciences,2008,178(22):4357-4374.
[19] 周欣,赵彬.m-半格的模糊理想 [J].西北大学学报,2015,45(2):202-206.(ZHOU Xin,ZHAO Bin.Fuzzy Ideals ofm-Semilattices [J].Journal of Northwest University,2015,45(2):202-206.)
[20] YANG Lingyun,XU Luoshan.Roughness in Quantales [J].Information Sciences,2013,220:568-579.
[21] LUO Qingjun,WANG Guojun.Roughness and Fuzziness in Quantales [J].Information Sciences,2014,271:14-30.
[22] Rodabaugh S E.Relationship of Algebraic Theories to Powersets over Objects in Set and Set×C [J].Fuzzy Sets and Systems,2010,161(3):453-470.
(责任编辑:赵立芹)
RoughFuzzyIdealsofm-Semilattices
ZHOU Xin,ZHAO Bin
(CollegeofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710062,China)
Using rough set theory,we proposed the congruences induced by fuzzy (prime)ideals of anm-semilattice and studied the properties of the upper (lower)rough fuzzy approximation operators with respect to these congruences.Then we introduced the notions of rough fuzzy (prime)ideals ofm-semilattices,and established the relationships between rough fuzzy (prime)ideals and fuzzy (prime)ideals and the relationships between rough fuzzy (prime)ideals and (prime)ideals ofm-semilattices.
m-semilattice;upper (lower)rough fuzzy approximation operator;(fuzzy)ideal;rough fuzzy (prime)ideal
10.13413/j.cnki.jdxblxb.2015.03.15
2014-10-09.
周 欣(1986—),女,汉族,博士研究生,从事格上拓扑与模糊推理的研究,E-mail:sxxzx1986@163.com.通信作者:赵 彬(1965—),男,汉族,博士,教授,博士生导师,从事格上拓扑与模糊推理的研究,E-mail:zhaobin@snnu.edu.cn.
国家自然科学基金(批准号:11171196;11301316)和中央高校基本科研业务费专项基金(批准号:GK201302003;GK201501001).
O153.1
:A
:1671-5489(2015)03-0429-10

