具有临界非线性项的p-双调和方程无穷多小解的存在性

苗凤华,宋玥蔷，周晨星

(1.长春师范大学 数学学院,长春 130032;2.长春师范大学 科研处,长春 130032)



具有临界非线性项的p-双调和方程无穷多小解的存在性

苗凤华1,宋玥蔷2，周晨星1

(1.长春师范大学 数学学院,长春 130032;2.长春师范大学 科研处,长春 130032)

利用一个新的对称山路引理研究一类具有临界非线性项的p-双调和方程,得到了该问题无穷多个非平凡解的存在性,并证明了这些解序列趋近于零.

p-双调和方程;对称山路引理;无穷多解

0 引 言

考虑如下p-双调和方程:

(1)

其中:Ω⊂N是一个有界光滑区域称为p-双调和算子,当p=2时为通常的双调和算子;p*=Np/(N-2p)为如下Sobolev嵌入的临界指标:

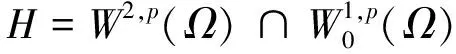
(2)

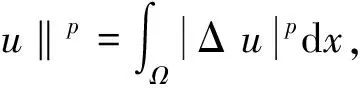
目前,关于临界指数增长问题解的研究已取得了许多结果[1-7].但对含有p-双调和算子问题的研究报道较少[8-10],特别是对带有临界非线性项的p-双调和算子无穷多个小解存在性的研究目前尚未见报道.本文利用一个新的对称山路引理[11]研究问题(1),获得了问题(1)无穷多个小解的存在性,并且这些解趋近于零.利用集中紧性原理[12]克服嵌入失去紧性条件所带来的困难,利用文献[13]中截断方法克服本文中非线性项是强不定的导致对称山路引理不能直接应用的困难.

假设f(x,u)满足下列条件:

(H1)f(x,u)∈C(Ω×,),对任意的u∈,f(x,-u)=-f(x,u);

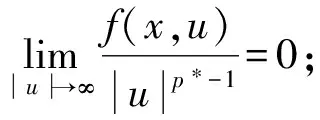
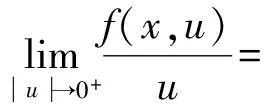
成立,则称u∈H是问题(1)的一个弱解.

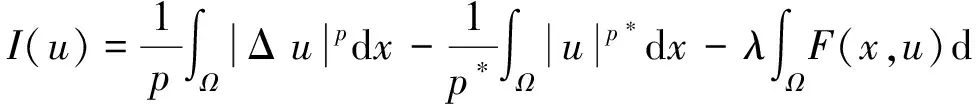
利用标准证明方法,可以证明泛函I∈C1(H,),并且泛函I对应的临界点正好对应问题(1)的解.

1 紧性条件

(3)

进而存在某个依赖于ε的正常数c(ε)>0,使得下列不等式成立:

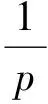
(4)

引理1假设条件(H1)～(H3)成立,则对任意的λ>0,泛函I满足(PS)c条件,这里

证明:令{un}为函数空间H中的(PS)序列,则由式(4)可得

于是,取定ε=(p*-p)/(2pp*λ)可知

(5)

其中o(1)→0,且M是某个正常数.另一方面,由式(3)可得

(6)

不等式(5),(6)表明,(PS)序列{un}在空间H中有界.从而可抽取子列,不妨仍记为{un},使得un⇀u弱收敛于H,un→u几乎处处收敛于Ω,

(7)

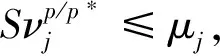
(8)

另一方面,由Hölder不等式和序列{un}的有界性可知

(9)

类似地,下列极限成立:

(10)

因此,由估计式(8)～(10)可得

(11)

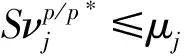
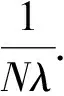
这里用到I′(u)=0,从而可知序列{un}在空间H中强收敛到u.

2 主要结果

设X是一个Banach空间,记

Σ∶={A⊂X{0}:A是闭的并且在X中关于原点对称}.

若A∈Σ,定义亏格γ(A)为

γ(A)∶=inf{m∈:∃φ∈C(A,Rm{0}),-φ(x)=φ(-x)}.

如果对任意的m∈,不存在如上定义的φ,则约定γ(A)=+∞.令Σk为X中所有闭对称子集A的全体,使得0∉A且γ(A)≥k.

引理2(对称山路引理)[11]设E是一个无限维空间,I∈C1(E,),如果下列条件成立:

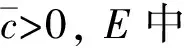
2)对每个k∈,存在Ak∈Σk,使得

则下列结论成立:

(i)存在序列{uk},使得I′(uk)=0,I(uk)<0,并且{uk}趋于零;

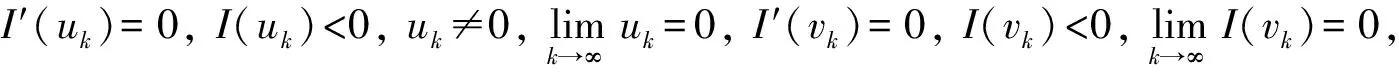
其中A,B,C是某些正的常数.

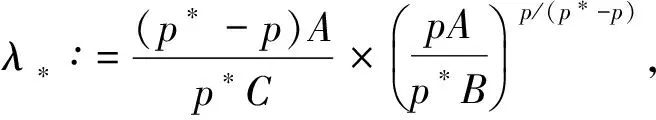
则易知χ(t)∈[0,1],并且χ(t)是C∞.令φ(u)=χ(‖u‖),考虑I(u)的扰动:

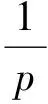
(12)

因此,可得:

引理3设G(u)由式(12)定义,则下列结论成立:

1)G∈C1(H,),G是偶的并且有下界;

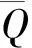
引理4假设条件(H3)成立,则对任意的k∈,存在δ=δ(k)>0,使得γ({u∈H:G(u)≤-δ(k)}{0})≥k成立.

证明:证明方法类似于文献[4],故略.

定理1假设条件(H1)～(H3)成立,则存在λ*>0,使得对任意的λ∈(0,λ*),问题(1)有一列非平凡解{un},且当n→∞时,un→0.

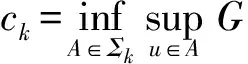
注1如果定理1中没有对称性条件(即f(x,-u)=-f(x,u)),则可利用本文方法得到至少一个非平凡解的存在性.

[1] Brezis H,Nirenberg L.Positive Solutions of Nonlinear Elliptic Equations Involving Critical Exponents [J].Commun Pure Appl Math,1983,36(4):437-477.

[2] LI Shujie,ZOU Wenming.Remarks on a Class of Elliptic Problems with Critical Exponents [J].Nonlinear Anal,1998,32(6):769-774.

[3] CHEN Jianqing,LI Shujie.On Multiple Solutions of a Singular Quasilinear Equation on Unbounded Domain [J].J Math Anal Appl,2002,275(2):733-746.

[4] HE Xiaoming,ZOU Wenming.Infinitely Many Arbitrarily Small Solutions for Sigular Elliptic Problems with Critical Sobolev-Hardy Exponents [J].Proc Edinb Math Soc,2009,52(1):97-108.

[5] Silva E A B,Xavier M S.Multiplicity of Solutions for Quasilinear Elliptic Problems Involving Critical Sobolev Exponents [J].Ann Inst H Poincaré Anal Non Linéaire,2003,20(2):341-358.

[6] Ghoussoub N,Yuan C.Multiple Solutions for Quasi-linear PDEs Involving the Critical Sobolev and Hardy Exponents [J].Trans Amer Math Soc,2000,352:5703-5743.

[7] Chabrowski J.On Multiple Solutions for the Nonhomogeneousp-Laplacian with a Critical Sobolev Exponent [J].Differ Integ Equ,1995,8(4):705-716.

[8] Candito P,Li L,Livrea R.Infinitely Many Solutions for a Perturbed Nonlinear Navier Boundary Value Problem Involving thep-Biharmonic [J].Nonlinear Anal,2012,75(17):6360-6369.

[9] LI Chun,TANG Chunlei.Three Solutions for a Navier Boundary Value Problem Involving thep-Biharmonic [J].Nonlinear Anal,2010,72(3/4):1339-1347.

[10] WANG Weihua,ZHAO Peihao.Nonuniformly Nonlinear Elliptic Equations ofp-Biharmonic Type [J].J Math Anal Appl,2008,348(2):730-738.

[11] Kajikiya R.A Critical Point Theorem Related to the Symmetric Mountain Pass Lemma and Its Applications to Elliptic Equations [J].J Funct Analysis,2005,225(2):352-370.

[12] Lions P L.The Concentration Compactness Principle in the Calculus of Variations.The Locally Compact Case Ⅰ [J].Ann Inst H Poincaré Anal Non Linéaire,1984,1(2):109-145.

[13] Garcia A J,Peral A I.Multiplicity of Solutions for Elliptic Problems with Critical Exponent or with a Nonsymmetric Term [J].Trans Amer Math Soc,1991,323(2):877-895.

[14] Willem M.Minimax Theorems [M].Boston:Birkhäluser Boston,Inc,1996.

(责任编辑：赵立芹)

ExistenceofInfinitelyManySmallSolutionsforp-BiharmonicEquationwithCriticalNonlinearity

MIAO Fenghua1,SONG Yueqiang2，ZHOU Chenxing1

(1.CollegeofMathematics,ChangchunNormalUniversity,Changchun130032,China;2.DepartmentofScientificResearch,ChangchunNormalUniversity,Changchun130032,China)

A class ofp-biharmonic equations with critical nonlinearity to obtain infinitely many solutions by means of a version of the symmetric mountain pass theorem.Finally,we showed that this sequence of solutions converge to zero.

p-biharmonic equation;symmetric mountain pass theorem;infinitely many solutions

10.13413/j.cnki.jdxblxb.2015.03.04

2014-08-04.

苗凤华(1968—),女,汉族,硕士,副教授,从事微分方程的研究,E-mail:mathfhmiao@163.com.通信作者:宋玥蔷(1980—),女,汉族,硕士,从事微分方程的研究,E-mail:songyueqiang@sohu.com.

国家自然科学基金(批准号:11301038)、吉林省科技厅青年基金(批准号:20130522100JH)、吉林省教育厅“十二五”科学技术研究项目(批准号:吉教科合字[2013]第252号)和吉林大学符号计算与知识工程教育部重点实验室开放课题基金(批准号:93K172013K03).

O175.2

：A

：1671-5489(2015)03-0367-05