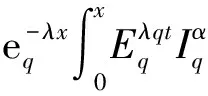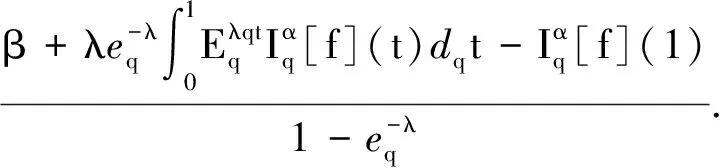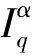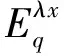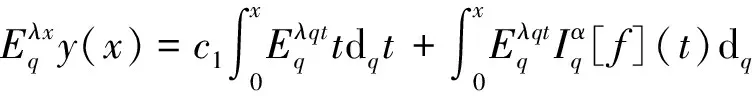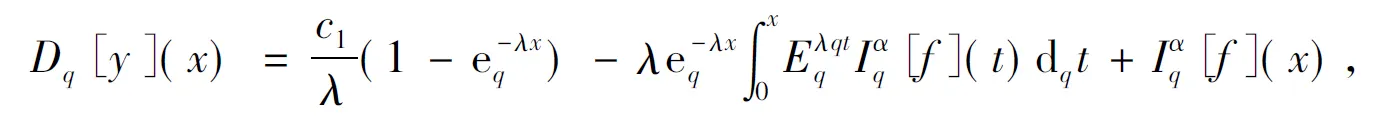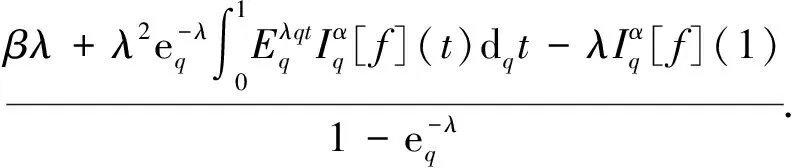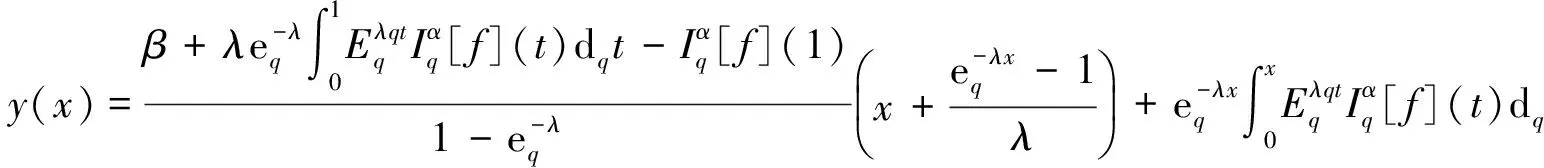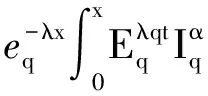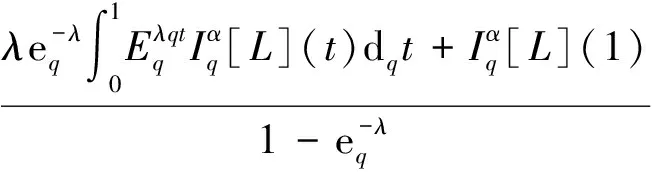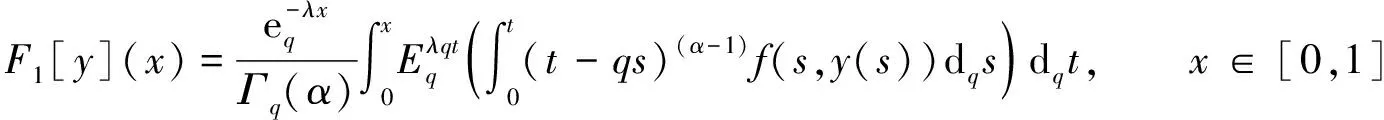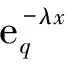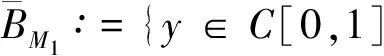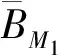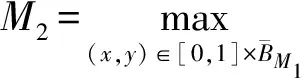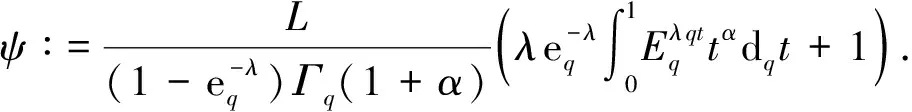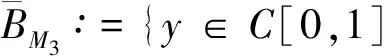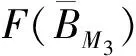一类有序分数阶q-差分方程解的存在性
葛 琦,侯成敏
(延边大学 理学院,吉林 延吉 133002)
一类有序分数阶q-差分方程解的存在性
葛 琦,侯成敏
(延边大学 理学院,吉林 延吉 133002)
考虑一类有序分数阶q-差分方程解的存在性和唯一性.先利用q-指数给出该方程解的表达式,再分别利用Banach压缩映像原理、Krasnoselskii不动点定理、Leray-Schauder选择定理证明该方程解的存在性和唯一性.
有序分数阶q-差分;不动点定理;解的存在性
0 引 言
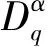
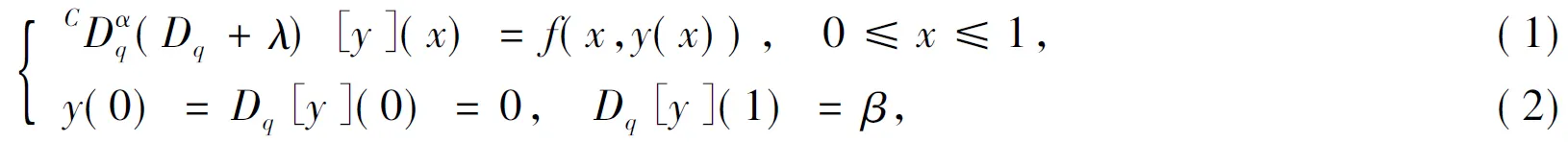
其中:1<α<2;0<λ<1;β>0;f∈C([0,1]×,)表示Caputo型分数阶q-导数(0 定义2[9]函数f(x)在区间[0,b]上的q-积分定义为 定义3[9]Riemann-Liouville型分数阶q-积分定义为 Caputo型分数阶q-导数定义为 引理1[9]设α≥0,I是包含原点的实区间,且a,b∈I,f(x),g(x)是定义在I到上的函数,则: 2)[a(x-t)](α)=aα(x-t)(α),xDq(x-t)(α)=[α]q(x-t)(α-1); 3)Dq[fg](x)=Dq[f](x)g(x)+f(qx)Dq[g](x); 这里iDq表示与变量i有关的q-导数. 定义4[10]定义标准q-指数函数如下: 其中:q>0;z是复数; [n]!=[1][2]…[n]; [k]=1+q+q2+…+qk-1; 引理2[9]如果f:[0,1]→是连续函数,则Iq[f]是连续函数. 引理3(Banach压缩映像原理)[11]设X是实Banach空间E上的非空闭子集,T:X→X是压缩算子,则T在X内存在唯一的不动点. 引理4(Krasnoselskii不动点定理)[11]设K是Banach空间E的有界凸闭子集,而T,S:K→E满足: 1)对任意x,y∈K有Tx,Tx+Sy∈K; 2)T是压缩映像; 3)S在K上是全连续的. 则T+S在K内至少存在一个不动点. 2)存在一个x∈∂U,对于λ∈(0,1)有x=λTx. 引理6(Arzela-Ascoli定理)[9]设D⊆n是一个有界域,如果K⊆)有界,且对于任意的ε>0,存在δ>0,使得‖x-y‖<δ⟹|u(x)-u(y)|<ε,∀∀u∈K,则是紧的. 引理7方程(1)-(2)与如下积分方程等价: 其中 (3) 由y(0)=Dq[y](0)=0,得c0=0.由于 所以 又由于 因此 于是 从而有 进而由Dq[y](1)=β得 因此 为了证明方程(1)-(2)解的存在性和唯一性,对Banach空间C([0,1],)赋范数‖y‖|y(x)|,对于y∈C([0,1],),定义C([0,1],)上的算子F: (4) 其中Ky定义见式(3). 定理1假设存在一个q-可积的函数L:[0,1]→,使得对于∀x∈[0,1]及∀y1,y2∈,有 |f(x,y1)-f(x,y2)|≤L(x)|y1-y2|, 设 如果Ω<1,则方程(1)-(2)有唯一解. 证明:先证明由式(4)定义的算子F是一个压缩映射.事实上,对于∀y1,y2∈C([0,1],),有 因此,当Ω<1时,算子F是一个压缩映射.由引理3知方程(1)-(2)有唯一解. 特别地,当定理1中的函数L是常数时,即对∀x∈[0,1],L(x)=L,有 又由于 所以,可取 定理2假设: 1)存在一个q-可积的函数L:[0,1]→,使得对于∀x∈[0,1]及∀y1,y2∈,有|f(x,y1)-f(x,y2)|≤L(x)|y1-y2|; 2)存在一个连续函数G:[0,1]→,使得对于∀x∈[0,1]及∀y∈,有|f(x,y)|≤G(x); 则方程(1)-(2)至少有一个解. 证明:为应用引理4,定义函数 取正实数M1,满足 其次,类似定理1的证明,易证F2是压缩映射,即‖F2[y1]+F2[y2]‖≤ψ‖y1-y2‖. 定理3假设: 1)存在连续函数G1,G2:[0,1]→和单调递增的函数使得对于∀x∈[0,1]及∀y∈,有|f(x,y)|≤G1(x)φ(|y|)+G2(x); 2)存在一个正常数N满足 (5) 其中 则方程(1)-(2)至少有一个解. [1] Page D N.Information in Black Hole Radiation [J].Phys Rev Lett,1993,71(23):3743-3746. [2] Youm D.q-Deformed Conformal Quantum Mechanics [J].Phys Rev D,2000,62(9):095009. [3] Jackson F H.q-Difference Equations [J].Amer J Math,1910,32(4):305-314. [4] Ferreira R A C.Nontrivial Solutions for Fractionalq-Difference Boundary Value Problems [J].Electron J Qual Theory Differ Equ,2010(70):1-10. [5] Ferreira R A C.Positive Solutions for a Class of Boundary Value Problems with Fractionalq-Differences [J].Comput Math Appl,2011,61(2):367-373. [6] ZHAO Yulin,CHEN Haibo,ZHANG Qiming.Existence Results for Fractionalq-Difference Equations with Nonlocalq-Integral Boundary Conditions [J/OL].Advances in Difference Equations,2013,doi:10.1186/1687-1847-2013-48. [7] ZHAO Yulin,YE Guobing,CHEN Haibo.Multiple Positive Solutions of a Singular Semipositione Integral Boundary Value Problem for Fractionalq-Derivatives Equation [J/OL].Abstract and Applied Analysis,2013.http://dx.doi.org/10.1155/2013/643571. [8] 孙明哲,韩筱爽.一类分数阶q-差分边值问题的正解 [J].延边大学学报:自然科学版,2013,39(4):252-255.(SUN Mingzhe,HAN Xiaoshuang.Positive Solutions for a Class of Boundary Value Problems with Fractionalq-Differences [J].Journal of Yanbian University:Natural Science,2013,39(4):252-255.) [9] Almeida R,Martins N.Existence Results for Fractionalq-Difference Equations of Orderα∈[2,3] with Three-Point Boundary Conditions [J].Commun Nonlinear Sci Numer Simul,2014,19(6):1675-1685. [11] 时宝,张德存,盖明久.微分方程理论及其应用 [M].北京:国防工业出版社,2005:4;14.(SHI Bao,ZHANG Decun,GAI Mingjiu.The Theory and Application of Differential Equations [M].Beijing:National Defense Industry Press,2005:4;14.) [12] WANG Jinhua,XIANG Hongjun,LIU Zhigang.Positive Solution to Nonzero Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations [J/OL].Int J Differ Equ,2010.http://dx.doi.org/10.1155/2010/186928. (责任编辑:赵立芹) ExistenceofSolutionsforaClassofSequentialFractionalq-DifferencesEquation GE Qi,HOU Chengmin (CollegeofScience,YanbianUniversity,Yanji133002,JilinProvince,China) We studied the existence and uniqueness of solutions for a class of the sequential fractionalq-differences equation.Firstly,a representation for the solution to this equation was given viaq-exponential.Then the existence and uniqueness of solutions were proven by means of Banach fixed point theorem,Krasnoselskii fixed point theorem and Leray-Schauder alternative theorem. sequential fractionalq-difference;fixed point theorem;existence of solutions 10.13413/j.cnki.jdxblxb.2015.03.06 2014-07-03. 葛 琦(1975—),女,汉族,硕士,副教授,从事微分方程理论及应用的研究,E-mail:geqi9688@163.com. 国家自然科学基金(批准号:11161049)和吉林省教育厅“十二五”科学技术研究项目. O175.6 :A :1671-5489(2015)03-0377-061 预备知识
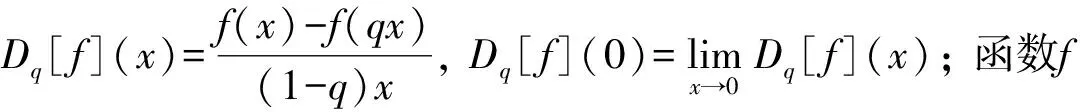
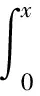
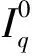

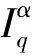
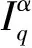
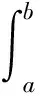

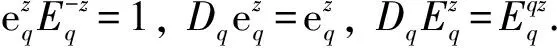

2 主要结果