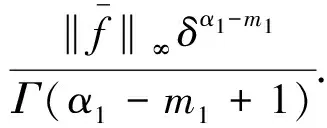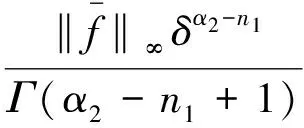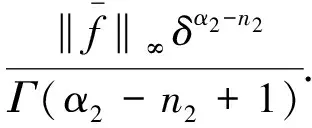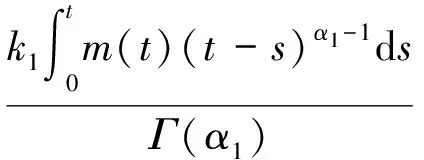一类具有初边值条件的非线性分数阶微分方程组解的存在性与唯一性
李雪梅,代 群,李辉来
(1.吉林大学 数学学院,长春 130012;2.长春理工大学 理学院,长春 130022)
一类具有初边值条件的非线性分数阶微分方程组解的存在性与唯一性
李雪梅1,代 群2,李辉来1
(1.吉林大学 数学学院,长春 130012;2.长春理工大学 理学院,长春 130022)
考虑一类具有初边值条件的耦合非线性分数阶微分方程组解的存在性与唯一性问题,应用Schauder和Banach不动点定理得到了此类方程组解的存在性与唯一性条件.
耦合方程组;分数阶微分方程;存在性;唯一性;Schauder不动点定理;Banach不动点定理
分数阶微分方程在工程技术以及各种材料和工艺的遗传特性描述中应用广泛[1-6].文献[7]讨论了一个具有边值条件的耦合分数阶微分方程;文献[8]分析了一种分数阶微分方程系统.本文考虑具有两点边值条件的分数阶微分方程组:
(1)
其中:0<αi≤1;0

定义2[10]令n-1<α≤n,n∈,则称为α阶Riemann-Liouville微分.
由分数阶积分和微分的定义可知IαIβf(t)=Iα+βf(t),DαIαf(t)=f(t).
引理1初边值问题(1)等价于如下方程组:
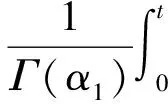
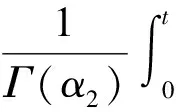
证明:对式(1)两边分别进行α1和α2次积分,得
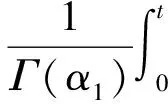
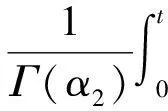
由于u(0)=0,v(0)=0,从而C1=C2=0,证毕.
定理1(存在性) 若fi:Wi→(i=1,2)连续,则初边值条件(1)有解(u(t),v(t)):[0,a*]→2.其中:
Wi=[0,a]×[Dmiu(0)-l1i,Dmiu(0)+l1i]×[Dniv(0)-l2i,Dniv(0)+l2i];
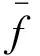
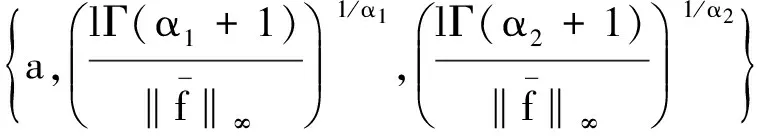
证明:令F(u(t),v(t))=(F1(u(t),v(t)),F2(u(t),v(t))),其中
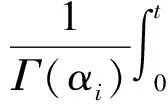
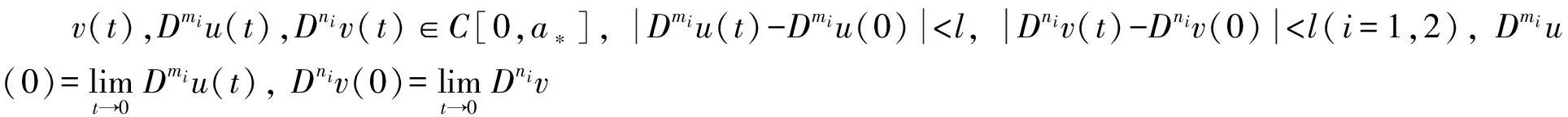
由于函数Dm1u(s),Dn1v(s),(t-s)αi-m1-1在[0,a*]上连续,则DmiF1(t)在[0,a*]连续.同理DniF2(t)在[0,a*]上连续.于是,有
同理|DniF2(t)-DniF2(0)| 从而F(u(t),v(t))是有界且逐点定义的. 且 因此,如果|t2-t1|<δ,则 同理,有 从而得F(U)是一个等度连续集,于是F是一个全连续算子,再由Schauder不动点定理知,F有一个不动点(u(t),v(t)):[0,a*]→为方程(1)的解. 定理2(唯一性)w=[0,a*]×[Dmiu(0)-l,Dmiu(0)+l]×[Dniu(0)-l,Dniu(0)+l],若fi(s,Dmiu(s),Dniv(s))(i=1,2)在w上连续,并存在两个正函数m(t),n(t)满足: 且如果 成立,则方程(1)有唯一正解.其中: 证明:由定理1可知F(U)⊆U, 而 类似地,有 则 ‖(Dm1u1(t),Dn1v1(t))-(Dm1u2(t),Dn1v2(t))‖∞≤k1‖(u1(t),v1(t))-(u2(t),v2(t))‖∞, 从而 同理有 |F2(u1(t),v1(t))-F2(u2(t),v2(t))|≤θ‖(u1(t),v1(t))-(u2(t),v2(t))‖∞, 则 |F(u1(t),v1(t))-F(u2(t),v2(t))|≤max{ρ,θ}‖(u1(t),v1(t))-(u2(t),v2(t))‖∞, 由定理1知F是全连续算子,又由Banach不动点定理可知,算子F在U中有唯一不动点,其即为方程组(1)的唯一正解. [1] BAI Zhanbing,LÜ Haishen.Positive Solutions for Boundary Value Problems of Nonlinear Fractional Differential Equations [J].Math Anal Appl,2005,311(2):495-505. [2] CHANG Yongkai,Nieto J J.Some New Existence Results for Fractional Differential Inclusions with Boundary Conditions [J].Math Comput Modelling,2009,49(3/4):605-609. [3] DENG Weihua.Numerical Algorithm for the Time Fractional Fokker-Planck Equation [J].J Comput Phys,2007,227(2):1510-1522. [4] BAI Chuanzhi,FANG Jinxuan.The Existence of a Positive Solution for a Singular Coupled System of Nonlinear Fractional Differential Equations [J].Appl Math Comput,2004,150(3):611-621. [5] CHEN Yong,AN Hongli.Numerical Solutions of Coupled Burgers Equations with Time- and Space-Fractional Derivatives [J].Appl Math Comput,2008,200(1):87-95. [6] Daftardar-Gejji V.Positive Solutions of a System of Non-autonomous Fractional Differential Equations [J].J Math Anal Appl,2005,302(1):56-64. [7] SU Xinwei.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations [J].Appl Math Lett,2009,22(1):64-69. [8] Daftardar-Gejji V,Babakhani A.Analysis of a System of Fractional Differential Equations [J].Math Anal Appl,2004,293(2):511-522. [9] Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations [M].Amsterdam:Elsevier,2006. [10] Podlubny I.Fractional Differential Equations [M].San Diego:Academic Press,1999. (责任编辑:赵立芹) ExistenceandUniquenessforaCoupledSystemofNonlinearFractionalDifferentialEquationswithInitialValueConditions LI Xuemei1,DAI Qun2,LI Huilai1 (1.CollegeofMathematics,JilinUniversity,Changchun130012,China;2.CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China) We studied a coupled system of nonlinear fractional equations with initial value condition and got the existence and uniqueness of it by means of the Schauder fixed point theorem and Banach fixed point theorem. coupled system;fractional differential equations;existence;uniqueness;Schauder fixed point theorem;Banach fixed point theorem 10.13413/j.cnki.jdxblxb.2015.03.03 2014-10-24. 李雪梅(1989—),女,汉族,硕士,从事偏微分方程的研究,E-mail:1304833191@qq.com.通信作者:李辉来(1962—),男,汉族,博士,教授,博士生导师,从事偏微分方程的研究,E-mail:lihuilai@mail.jlu.edu.cn. 国家自然科学基金(批准号:11271154). O175.08 :A :1671-5489(2015)03-0363-04