多车场公交乘务排班问题优化

陈明明,牛惠民

(兰州交通大学交通运输学院,兰州730070)

多车场公交乘务排班问题优化

陈明明,牛惠民*

(兰州交通大学交通运输学院,兰州730070)

公交乘务排班是公交智能化调度的重要研究内容.目前我国大多数城市排班主要采用人工经验,具有很大盲目性和繁琐性,且排班结果多为单车场的乘务组排班方案.本文以班次时间接续、乘务组劳动强度、车场能力等为约束条件,以最小化乘务组的车场驶入/驶出成本、停留等待成本和空驶成本为目标函数,建立了多车场公交乘务排班问题的数学模型.采用禁忌搜索算法求解模型,设计了初始生成解的启发式方法,提出了基于有序序列的班次交换和插入策略进行邻域搜索.选取两个车场范围内的四条公交线路为实例,进行仿真测算和数据分析.结果表明,利用本文模型得到的乘务排班结果能有效地处理多车场公交乘务组跨线排班问题.

城市交通;乘务排班;禁忌搜索算法;班次;多车场

1 引 言

乘务排班问题作为城市公交调度问题中的重要内容,主要是对乘务组一天内公交运营工作的安排.合理安排乘务排班计划,不仅能够有效利用人力资源,提高乘务工作效率,而且可以降低公交运营成本,提高公交管理水平,从而为公交管理部门决策提供科学依据.

公交乘务排班问题有较为广泛的研究,出现了许多模型和求解方法.Simth等提出了基于集覆盖问题的乘务排班模型,并用整数线性规划进行求解[1].Ceder将乘务排班方法归结为集分割问题,使用最短路径及匹配算法进行求解[2].Lourenco等提出了一种多目标的乘务排班模型,分别利用禁忌搜索和遗传算法进行求解[3].沈吟东等以乘务组数量最少和成本最低为目标建立了优化模型,设计了带时间窗的多邻域结构及禁忌搜索算法[4].陈明明等以乘务组总空闲时间最小为目标,建立了多班型的乘务排班模型[5].上述研究大多考虑单车场的公交乘务排班问题,较少对多车场公交乘务排班问题进行研究.

Boschetti等将多车场的车辆调度问题和单车场的乘务排班问题相结合,建立了基于集分割问题的数学模型,但目标函数中未考虑乘务组的空闲时间成本[6];Huisman等研究了多车场的车辆和人员统一调度模型,其中假定乘务组在执行连续班次间,若有充足时间将返回车场[7],这一假设有悖于我国目前公交调度实际情况;Kliewer等人建立了带有时间窗的多车场乘务调度模型[8],但模型未充分考虑公交车场的能力约束;钟石泉等分析了多车场车辆调度中能力、时间窗、多车型等约束的处理方法[9],但没有研究乘务组排班问题对多车场公交调度的影响.

基于以上考虑,本文将车场、乘务组和班次相结合,对多车场下的公交乘务排班过程进行阐述,提出相应的乘务排班优化模型和算法,求得最优排班方案,从而为多车场公交乘务跨线排班问题提供理论依据.

2 问题分析

本文以多条城市公交线路为研究对象,在公交运营时间内,每条线路一天所发班次的数量及每个班次在起始点的开始时刻和终点站的结束时刻均已确定.所有班次的时间安排构成了一天的公交运行时刻表.乘务组人员和车辆固定,中途不更换车辆.乘务组可选择从多个车场中的某一车场签到出发,执行一系列班次任务,最后返回同一车场进行签退,从而完成一天的运营工作任务,如图1所示.

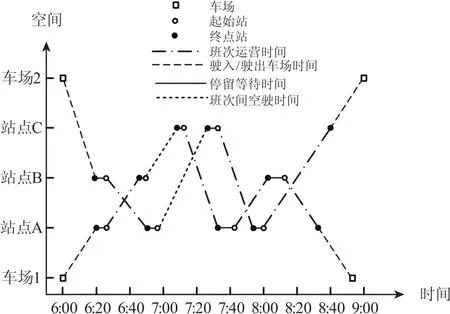
图1 乘务组运营工作示意图Fig.1 The operation diagram of crew

多车场乘务组排班问题就是根据一天给定的公交运行时刻表和乘务规则等,考虑一定的优化目标和约束条件,对乘务组的驶入驶出车场和执行班次链等做出具体的安排,以确保有效地完成所有的班次任务.

3 数学模型

3.1 符号及参数

定义建模所需的符号及参数如下:M为公交车场总数量;m为车场标记;N为公交时刻表规定的一天班次数量;i为班次标记;di为班次i在起始站的开始时刻;ai为班次i在终点站的结束时刻;k为乘务组标记;xim,k为0-1决策变量,若班次i由车场为m的乘务组k执行,取值为1,否则为0;为0-1变量,若车场为m的乘务组k执行班次任务i后,下一个执行任务为班次j,取值为1,否则为0.

为研究方便,本文采用将车场序号与班次序号相对应的方法,例如车场m的序号用N+m来表示。定义ti,j为乘务组从节点i到节点j的空驶时间,这里的节点可表示车场或班次的起讫点,例如tN+2,3表示乘务组从车场2到班次3起始站A的空驶时间;t3,5为乘务组在执行班次3和班次5之间的空驶时间;t5,N+2表示乘务组执行完班次5后返回车场2的空驶时间,如图2所示.

图2 乘务组空驶时间的表示Fig.2 The expression of deadheading

3.2 约束条件

(1)班次唯一性约束.

对于任意一个班次,仅能由唯一车场的乘务组执行且只执行一次.

对于两个接续班次,必须保证由同一乘务组执行,故有

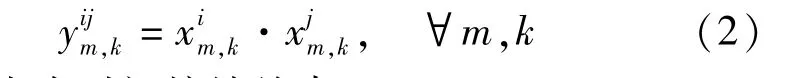
(2)班次时间接续约束.

在乘务组执行的连续班次中,当前班次的终点站与后一班次的起始站处于相同站点时,该班次间不存在空驶;否则产生空驶.定义δi,j为0-1辅助变量,当班次i与j之间有空驶,其值为1;否则其值为0.

式中 Start(i)表示班次i的起始站;End(i)表示班次i的终点站.

班次时间接续约束,即乘务组执行的相邻两个班次中,后一班次的开始时刻和前一班次的结束时刻相差应不小于最小停留时间T0.对于有空驶现象的连续班次,还应考虑空驶时间约束,则有

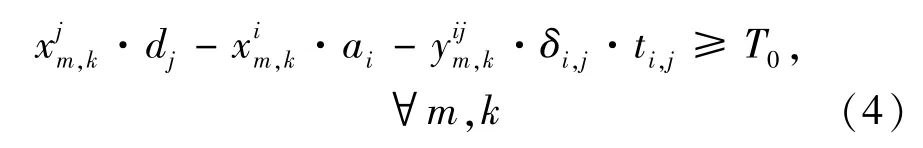
(3)乘务组劳动强度约束.

乘务组劳动强度约束,即每个乘务组一天的累计工作时间不应超过规定的最长工作时间T1,故有

(4)车场能力约束.

对于车场m,一天实际的乘务组数量取决于从该车场驶出的乘务组数量,计算如下

由于假设每个乘务组与车辆相对应,中途不更换车辆,因此,车场对公交车辆的能力约束也就转换为对乘务组的能力约束,即

式中 ψm为车场m一天能安排的最大乘务组数量.

3.3 目标函数

乘务组的成本包括班次运营成本、驶入/驶出车场成本、班次间空驶成本和停留等待成本.乘务排班的优化目标是使乘务组的总成本最小.由于每个班次的运营时间固定,不同乘务排班方案中班次运营成本均相同,在优化目标中可忽略该成本因素.驶入/驶出车场成本取决于乘务组从车场驶出到第一个班次起始站的空驶时间,以及从最后一个班次的终点站至驶入车场的空驶时间.则对于车场m的第k个乘务组,其驶入/驶出车场的空驶成本为

式中 ωd为乘务组的单位空驶成本;

对于车场m的第k个乘务组,班次间的总空驶成本为

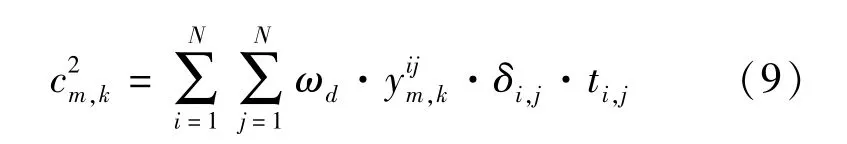
停留等待时间是指乘务组执行下一班次的开始时刻与上一班次结束时刻的时间差。当班次间存在空驶,应减去空驶时间.则对于车场m的第k个乘务组,停留等待总成本为

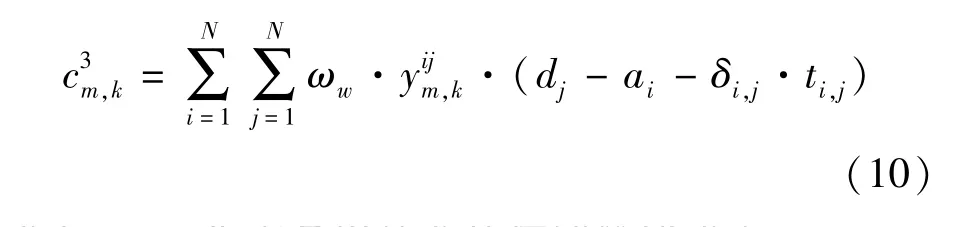
式中 ωw为乘务组的单位停留等待成本.

基于以上分析,该数学模型的目标函数为

4 算法设计

禁忌搜索算法是一种基于邻域搜索的算法,通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索,并通过藐视准则来赦免一些被禁忌的优良状态,进而保证多样化的有效搜索以最终实现全局优化.本文所构建的多车场乘务排班模型是一个复杂的0-1规划问题,可用禁忌搜索算法进行求解.算法的主要参数设计如下.

4.1 解的表示形式

乘务排班问题的解,可采用二维整数型数组进行编码,其中行表示乘务组,第一列元素的值表示乘务组所属车场编号,其余列元素的值为乘务组的执行班次,班次按自然数列升序排列.假定5个乘务组执行18个班次,问题解的表示形式如图3所示.

图3 解的表示形式Fig.3 The expression of solution

解码是根据二维数组中数值对问题的解进行操作.以图3中数据为例,由于所有乘务组共从两个车场驶入/驶出,第一个车场的乘务组数量为2,由序号为1和2的乘务组执行,执行班次分别为1-1-4-8-12和1-2-5-9,则变量.第二个车场乘务组的解码方法同理可得,如图4所示.

图4 解码示意图Fig.4 The decoding of solution

4.2 初始解的生成

初始解决定算法搜索的起始点,质量优的初始解能使算法快速收敛到最优解.在初始解生成过程中,考虑班次时间接续和乘务组劳动强度约束,设计如下贪婪启发式算法。

Step 1 初始化,令车场m的第k个乘务组所完成的班次集合

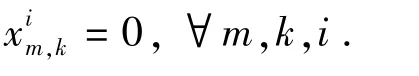
Step 2 确定执行班次i的乘务组所对应的车场序号

Step 3 确定执行班次i的乘务组编号k和最大班次序号.若sm＞ 0,则,转Step 4;否则转Step 6.

Step 4 班次时间接续检验,若di-ai′-δi′,i·,则转Step 5;否则转Step 6.

Step 5 乘务组劳动强度检验,令车场m的第k个乘务组的总工作时间+ai-di,若Zm,k≤T1,则转Step 7;否则转Step 6.

Step 6 令sm←sm+1,k←sm,转Step 7.

Step 8 若i＞N,算法终止,输出结果;否则转Step 2.

4.3 邻域结构

采用乘务组间班次的交换与插入策略.班次交换策略,即从乘务组1和乘务组2中各选一个班次进行交换.例如将乘务组1:1-1-4-8-12的班次4和乘务组2:1-2-5-9的班次5进行交换,可得到新解:乘务组1:1-1-5-8-12和乘务组2:1-2-4-9,如图5所示.

班次插入策略,即将乘务组1的一个班次插入到乘务组2,插入位置依据乘务组2中班次序号升序排列.例如将乘务组1:1-1-4-8-12中的班次4插入到乘务组2:1-2-5-9中,可得新解:乘务组1:1-1-8-12和乘务组2:1-2-4-5-9,如图6所示.交换或插入后的乘务排班结果若不满足时间接续和劳动强度约束,则不进行该操作.

4.4 禁忌表、禁忌长度、藐视准则及终止条件

禁忌表中记录的是变换(交换和插入)的节点,禁忌长度采用固定长度.选取基于评价值的规则作为藐视准则,即若出现一个解的目标值好于前面任何一个最佳候选解,可特赦.终止准则采用目标控制原则,如果在一个给定步数内,当前最优值

没有变换,终止计算.

图5 班次交换策略Fig.5 Trips exchange strategy

图6 班次插入策略Fig.6 Trips insert strategy

4.5 解的评价

为使算法在迭代过程中不断搜索到更优解,需进行解的评价.在评价中既要计算目标函数值,又要考虑约束条件.由于初始解已满足时间接续、劳动强度约束,且在邻域搜索过程中生成的新解也都满足该约束,故在解的评价中仅需考虑车场能力约束.在计算适应值时,需对不满足车场能力约束的解进行惩罚,采用的适应值函数为

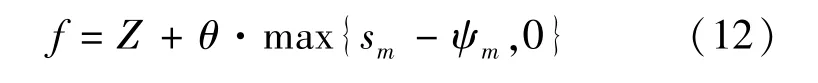
5 算例研究

为研究方便,本文将一条公交线路按上下行方向划分为两条不同的公交线路,则起讫点A、B和B、C之间共有四条公交线路(L1、L2、L3、L4),如图7所示.乘务组可从两个车场中任一车场驶出至首发班次的起始站,从结束班次的终点站返回至出发车场.四条公交线路一天共337个班次,每个班次所属线路及开始时刻已知,如表1所示.L1、L2线路的运行时间均为25 min,L3、L4线路间的运行时间均为30 min.站点A与站点B、站点C、车场1、车场2之间的空驶时间分别为10 min、16 min、 8 min、15 min;站点B与站点C、车场1、车场2之间的空驶时间分别为20 min、15 min、10 min;站点C与车场1、车场2之间的空驶时间分别为18 min、12 min.

图7 多车场公交线路运行示意图Fig.7 Bus lines with multiple depots

从表1可以看出,不同线路一天所发班次总数差异较大,线路L1全天共有107个班次,且在早高峰(7:00-9:00)平均发车间隔为5 min;线路L2共有108个班次,在晚高峰(18:00-20:00)平均发车间隔为5 min;线路L3和L4全天分别有59和63个班次,平均发车间隔分别为15 min和14 min.

车场1和车场2一天能安排的最大乘务组数量分别为10和25,乘务组的单位空驶成本和单位停留等待成本分别为2元/min和0.4元/min.乘务组班次间的最小停留时间为3 min,累计工作时间不超过480 min.禁忌搜索算法的参数设置为:禁忌长度为6,最大迭代次数为800,惩罚因子取值为10 000.应用VC++编程得到最优解如表2所示.

表1 班次开始时刻表及所属线路Table 1 Departure time and line number of trips

表2 乘务排班优化方案Table 2 The optimal result of crew scheduling

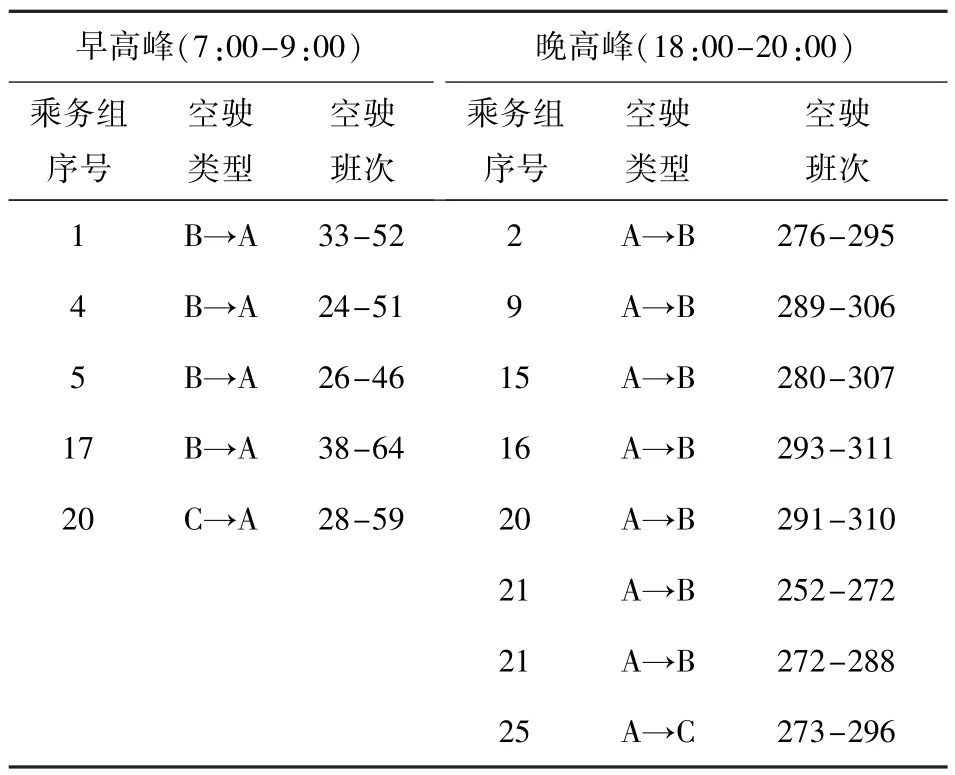
表3 高峰时段乘务组空驶结果Table 3 The deadheading trips during peak hours

根据表2中的乘务排班优化方案,可推算出早晚高峰时段乘务组空驶班次结果,如表3所示.在早高峰时段,L1线路(A→B)发车间隔较小,在乘务组数量有限的情况下,势必需要其余线路乘务组空驶到L1线路的起始站A,本例中共有5个空驶班次分别从站点B和站点C到达站点A,从而在不需增加乘务组总数的前提下,解决了L1线路早高峰的运力紧张问题;在晚高峰时段,L2线路(B→A)发车频率较大,则需其余线路乘务组空驶到L2线路的起始站B,而此时L1线路(A→B)发车间隔较大,通过7个空驶班次从L1线路的始发站A到达站点B,有效地解决了L2线路晚高峰的供需不平衡问题.

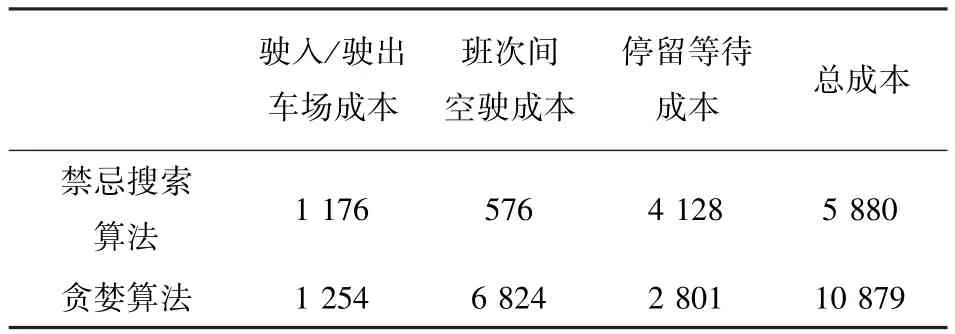
表4 禁忌搜索算法与贪婪算法计算结果对比Table 4 Comparison of computing results using tabu

表4对比了运用禁忌搜索算法和贪婪算法计算得到的乘务排班方案成本,显然禁忌搜索算法得到的总成本要远低于贪婪算法的总成本.贪婪算法结果中班次间空驶成本占总成本的62.7%,这是由于排班方案仅考虑了班次接续约束和乘务组劳动强度约束,未考虑不同成本类型对目标值的影响.禁忌搜索算法得到的排班优化方案,停留等待成本占乘务组总成本的70.2%,空驶成本仅占9.8%.该算法通过班次交换策略改变了乘务组所执行班次链的结构,使乘务组班次间的空驶数量减少,从而有效降低了班次间的总空驶成本;班次插入策略改变了乘务组所执行班次数量,优化了乘务组驶入/驶出车场成本和停留等待成本,避免算法陷入局部最优.因此通过禁忌搜索算法可以进一步优化排班方案,提高解的质量,验证了该算法的有效性.

6 研究结论

本文以公交区域调度中的车场、乘务组和班次为研究对象,考虑了车场能力、乘务组劳动强度、班次时间接续等约束,以最小化乘务组的驶入/驶出成本、空驶成本、停留等待成本为目标函数,建立了多车场下公交乘务排班模型及相应的禁忌搜索算法,并运用实例进行仿真计算.结果表明,该模型适用于客流具有明显潮汐特性的公交线路,可以有效地解决多车场约束下乘务组跨线排班问题.此外,模型通过整合不同车场的车辆和乘务组资源,在一定区域范围内将多个车场的车辆和乘务组人员相协调,高效地完成多条公交线路的所有班次任务,实现资源的有效配置和充分利用.考虑带有时间窗和不同班型条件下的多车场公交乘务组排班问题,将是下一步研究的方向.

[1] Smith B M,Wren A.A bus crew scheduling system using a set covering formulation[J].Transportation Research,1988(22A):97-108.

[2] Avishai Ceder.Public transit planning and operation——Theory,modelingandpractice[M].London: Butterworth-Heinemann,2007.

[3] Lourenco H R,Paixao J P,Portugall R.Multiobjective metaheuristics for the bus-driver scheduling problem [J].Transportation Science,2001,35(3):331-343.

[4] 沈吟东,倪郁东.含时间窗的司售员调度模型及多邻域结构设计[J].华中科技大学学报,2008(12): 31-34.[SHEN Y D,NI Y D.Model for crew scheduling with time windows and multi-neighborhood structures[J].Journal of Huazhong Univ.of Sci.& Tech.,2008(12):31-34.]

[5] Mingming Chen,Huimin Niu.A model for bus crew scheduling problem with multiple duty types[J]. Discrete Dynamics in Nature and Society,2012:1-12.

[6] Boschetti M A,Mingozzi A.An exact algorithm for the simplified multiple depot crew scheduling problem[J]. Annals of Operations Research,2004(127):177-201.

[7] Dennis Huisman,Richard Freling,P M Wagelmans. Multiple-depot integrated vehicle and crew scheduling [J].Transportation Science,2005(39):491-502.

[8] Natalia Kliewer,Bastian Amberg,Boris Amberg. Multiple depot vehicle and crew scheduling with time windows for scheduled trips[J].Public Transport, 2012,3(3):213-244.

[9] 钟石泉,贺国光.多车场有时间窗的多车型车辆调度及其禁忌算法研究[J].运筹学学报,2005(4): 67-73.[ZHONG S Q,HE G G.Study on multi-depot vehicle scheduling problem with time windows and multi-type vehicle limits and its tabu search algorithm [J].OR Transactions,2005(4):67-73.]

An Optimization Model for Bus Crew Scheduling with Multiple Depots

CHEN Ming-ming,NIU Hui-min
(School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China)

Crew scheduling is an important element of intelligent transit dispatching.The scheduling methods of many cities in China are mainly based on artificial experience with great blindness and tediousness.Moreover,the scheduling results are mostly focused on the field of crew scheduling with a single depot.A mathematical model of multiple depots crew scheduling is formulated with the time shift of trips, work intensity for crew,capacity of depots as constrains,and with the minimum cost of pull-in/pull-out time,waiting time and deadheading as the objective function.The tabu search algorithm is used to solve the proposed model,and a heuristic algorithm is designed to generate the initial solution.A neighborhood search method with trip exchange and insert strategy is also presented based on the ordered sequence.Taking four bus lines with two depots as examples,the proposed model can effectively solve the crew scheduling problem with multiple depots which allows vehicles and crew running at the cross-lines.

urban traffic;crew scheduling;tabu search algorithm;trips;multiple depots

U491

: A

U491

A

1009-6744(2013)05-0159-08

2013-04-10

2013-05-09录用日期:2013-05-20

国家自然科学基金项目(71261014).

陈明明(1982-),男,山西霍州人,博士生.

*通讯作者:hmniu@mail.lzjtu.cn