城市轨道交通侧式换乘站台最高聚集人数计算

王永亮,张星臣,蒋 洋,朱宇婷

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)

城市轨道交通侧式换乘站台最高聚集人数计算

王永亮,张星臣*,蒋 洋,朱宇婷

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)

运用趋势分析法计算某一时段内城市轨道交通线路衔接交路下侧式换乘站台最高聚集人数.界定相关研究条件,运用趋势分析法分析时间单元内乘客与列车、站台之间的交互过程,探讨换乘站台非换乘和换乘客流聚集人数变化过程;进而将两类客流聚集人数变化过程同步叠加,得出换乘站台最高聚集人数的计算公式.简单算例应用表明,本文提出的衔接交路下换乘站台最高聚集人数计算公式是可行的;与地铁设计规范计算方法相比,本文提出的计算方法所得结果相对准确.

城市交通;最高聚集人数;趋势分析法;侧式换乘站台;衔接交路

1 引 言

衔接交路,是若干长短交路的组合衔接[1](或交错),列车只在线路的某一区段内运行、在指定的中间站折返.采用衔接交路可以灵活制定各交路的列车运行图,从而提高各交路的列车满载率,并加快列车的周转.然而,上(下)行列车共用的换乘站台容易形成大客流聚集,较大的换乘比例将进一步加剧换乘站台的客流压力,降低城市轨道交通的服务水平.因此,如何准确计算衔接交路下换乘站台的最高聚集人数将直接影响换乘站台服务水平评价的可信度.

另外,站台聚集人数的计算,多在规划设计阶段进行,较少考虑后期运营组织的具体影响,本文将采用运行图作为输入条件,符合运营提前介入规划设计阶段的机制.

目前,有关城市轨道交通衔接交路下换乘站台最高聚集人数的研究[2-4]还处于起步阶段.文献[2]分析了不同能力与需求关系下,站台候车人数变化情况.文献[3]以单一交路下中间站站台为研究对象,提出列车到达间隔时间恒定条件下计算站台最高聚集人数的方法.文献[4]在不同交路列车开行比例均衡的基础上,对长短交路、支线运行和不同换乘方式下的站台聚集人数变化情况进行分析.文献[5]在所有列车运载属性相同的条件下,给出了换乘站台最高聚集人数的计算方法.

基于上述分析,针对车站上(下)行列车共用同一站台、不存在支线的城市轨道交通线路,本文以其衔接交路下侧式换乘站台为研究对象,基于已知的运行图,运用趋势分析法计算侧式换乘站台最高聚集人数.算例应用表明:本文得出的计算方法是可行的,而且比文献[5]计算方法所得结果相对准确.

2 研究条件界定

2.1 假设条件界定

已知运行图条件下,本文研究基于如下假设:

(1)乘客严格遵循先下后上原则;

(2)进入站台乘车的乘客按均匀分布到达;

(3)列车停站时间内,站台上等候该列车的乘客没有滞留;

(4)前一列车运达的以换乘站为目的地的下车乘客全部离开站台时刻,早于当前列车的到站时刻;

(5)乘客上车速率大于进入站台乘车的乘客到达速率;

(6)换乘客流全部在换乘站台(目标换乘列车的始发站站台)换乘;

(7)同一车站上(下)行列车停站时间和乘客下车时间相同;

(8)同一区间上(下)行列车运行时间相同.

2.2 研究对象界定

衔接交路分交错衔接交路和同站衔接交路两类[1].本文以较为复杂的交错衔接交路(如图1所示)为例计算侧式换乘站台最高聚集人数,同站衔接交路的情况可类似确定.由于上、下行换乘站台聚集人数变化规律相同,因此,本文仅以上行侧式换乘站台为例计算站台最高聚集人数.

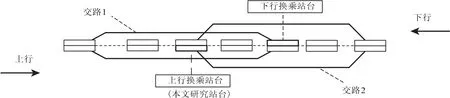
图1 交错衔接交路侧式换乘站台分布Fig.1 Transfer side-platform of crisscross joint routing

3 相关参数定义

T——换乘站台最高聚集人数研究时段(s);

t0——换乘站研究时段T的开始时刻(s);

tT——换乘站研究时段T的结束时刻(s);

N——研究时段内换乘站上行发车列数(列/T),i∈{1,2,…,N}为发车顺序;

h——研究时段内换乘站上行当前列车与前一列车之间的发车间隔(s);

j+1——交路1上行部分;

j+2——交路2上行部分;

xi——换乘站第i∈{1,2,…,N}列上行列车运行交路xi∈{j+1,j+2},当xi为j+1时,=1且=0,当xi为j+2时,=0且=1;

yi——换乘站第i∈{1,2,…,N}列上行列车发车时刻yi∈[t0,tT];

Ixi——换乘站第i∈{1,2,…,N}列上行列车前一交路xi列车的发车顺序,该前一列车不存在时,令Ixi=0且y0=t0;

I′xi——换乘站第i∈{1,2,…,N}列上行列车前一非交路xi列车的发车顺序,该前一列车不存在时,令I′xi=0且y0=t0,当I′xi为i-1时,=1;

qj+2,d——研究时段内仅j+2列车从上行换乘站台运走的客流量(人);

qt——研究时段内j+1列车运达上行换乘站台的换乘客流量(人);

ts——上行列车在换乘站的停站时间(s);

ta——上行列车在换乘站的乘客下车时间(s);

vo——以上行换乘站台为目的地的乘客的平均离开该站台速率(人/s);

to——从列车停站开始到以上行换乘站台为目的地的乘客全部离开该站台的时间(s);

vj+1,+2,i——研究时段内可乘坐j+1或j+2列车离开站台的乘客平均进入站台速率(人/s);

vj+2,i——研究时段内仅能乘坐j+2列车离开站台的乘客的平均进入站台速率(人/s);

vj+1,d——研究时段内乘坐j+1列车离开站台的乘客的平均上车速率(人/s);

vj+2,d——研究时段内乘坐j+2列车离开站台的乘客的平均上车速率(人/s);

vj+1,a——研究时段内乘坐j+1列车到达站台的乘客的平均下车速率(人/s);

qnt,i——上行换乘站台第i∈{1,2,…,N, N+1}个时间单元内站台非换乘客流最高聚集人数(人);

qt,i——上行换乘站台第i∈{1,2,…,N,N+ 1}个时间单元内站台换乘客流最高聚集人数(人);

qi——上行换乘站台第i∈{1,2,…,N,N+ 1}个时间单元内站台最高聚集人数(人);

qMAX——上行换乘站台最高聚集人数(人);

4 换乘站台最高聚集人数计算

为了更好地探讨侧式换乘站台聚集人数的变化过程,将研究时段T按发车列数N细分为N+1个时间单元,如图2所示.其中,第1个时间单元范围为:研究时段开始时刻t0开始,第1列车离站时刻y1结束;第2至N个时间单元范围为:前一列车离站时刻开始,当前列车离站时刻结束;第N+1个时间单元范围为:第N列车离站时刻yN开始,研究时段结束时刻tT结束.可以看出,当第N列车离站时刻与研究时段结束时刻tT重合时,第N+1个时间单元将不存在.

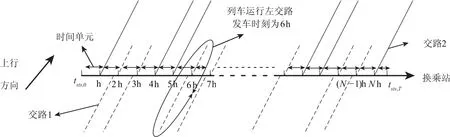
图2 换乘站上行列车运行交路及其发车时刻Fig.2 Up train routing and departing time of transfer

研究时段开始时刻t0的换乘站台聚集人数为0时,依据假设(3),第1个时间单元可合并到之后的2至N个时间单元进行处理.为简化计算,本文假设t0时刻换乘站台聚集人数为0.

采用趋势分析法计算侧式换乘站台最高聚集人数,研究思路如下:

通过分析任一时间单元内站台上车非换乘乘客、站台下车非换乘乘客、进入站台乘客、离开站台乘客、站台下车换乘客流、站台上车换乘客流的活动时间及其人数变化趋势,理解乘客与列车、站台之间的交互过程,把握换乘站台非换乘和换乘客流聚集人数变化过程;进而将两类客流聚集人数变化过程进行同步叠加,得出换乘站台最高聚集人数的计算公式.

4.1 非换乘客流聚集人数变化过程

站台非换乘客流聚集人数变化过程包含前N个、第N+1个时间单元两部分,其中,前N个时间单元内任一时间单元对应的当前列车为j+1列车或j+2列车.

4.1.1 前N个时间单元

依据参考文献[3]及假设(5),存在以下大小关系:

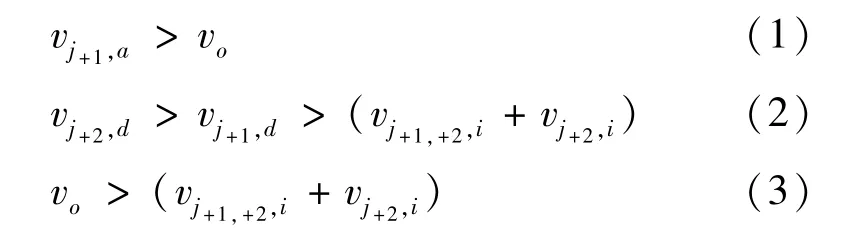
任一时间单元内站台非换乘客流聚集人数变化过程如图3所示,图中t1为前一j+1列车运达的以上行换乘站台为目的地的乘客全部离开该站台的时刻to-ts;t2为列车到站时刻h-ts;t3为停站时间内乘客开始上车时刻h-ts+ta.

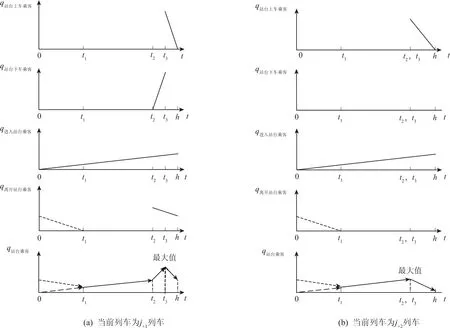
图3 任一时间单元内站台非换乘客流聚集人数变化过程Fig.3 Noninterchange passenger flow assembling change process for time element

(1)当前列车为j+1列车.

从图3(a)可以看出,当前列车为j+1列车时站台聚集人数变化趋势如表1所示.任一时间单元内站台非换乘客流最高聚集人数qnt,i出现在t3时刻,为该时刻已进入站台的等待出发客流量与站台下车客流量中未离开站台部分之和.

表1 当前列车为j+1列车时站台聚集人数变化趋势Table 1 Assembling change trend for j+1train

等待出发客流量包含等待j+1或j+2列车客流、等待j+2列车客流两部分,其中,等待j+1或j+2列车客流的聚集时间段为:当前时间单元0-t3时间段;等待j+2列车客流的聚集时间段为:前一j+2列车离站时刻开始,当前时间单元t3时刻结束.

站台下车客流量为j+1列车已停站站台上乘坐当前列车的以上行换乘站台为目的地的出发客流量之和,而这些出发客流量的聚集时间段为:停站站台当前j+1列车与前一j+1列车之间的发车间隔;依据假设(2)、(7)、(8),对于上行换乘站台和已停站站台来说,当前j+1列车与前一j+1列车之间的发车间隔是相同的;因此,乘坐当前j+1列车下车客流量的聚集时间段为:上行换乘站台前一j+1列车离站时刻开始,当前j+1列车离站时刻结束.

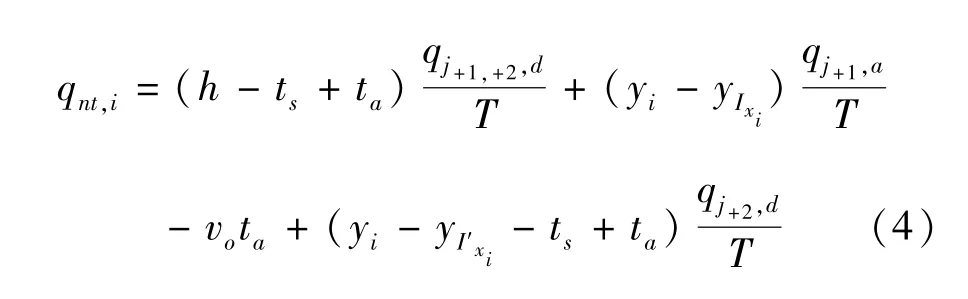
(2)当前列车为j+2列车.

从图3(b)可以看出,任一时间单元内,列车到站时刻t2与停站时间内乘客开始上车时刻t3重合,当前列车为j+2列车时站台聚集人数变化趋势如表2所示.任一时间单元内站台非换乘客流最高聚集人数qnt,i出现在t2/t3时刻,为该时刻已进入站台的等待出发客流量.

表2 当前列车为j+2列车时站台聚集人数变化趋势Table 2 Assembling change trend for j+2train

等待出发客流量包含等待j+1或j+2列车客流、等待j+2列车客流两部分,其中,等待j+1或j+2列车客流的聚集时间段为:当前时间单元0-t2/t3时间段;等待j+2列车客流的聚集时间段为:前一j+2列车离站时刻开始,当前时间单元t /t时刻结束.

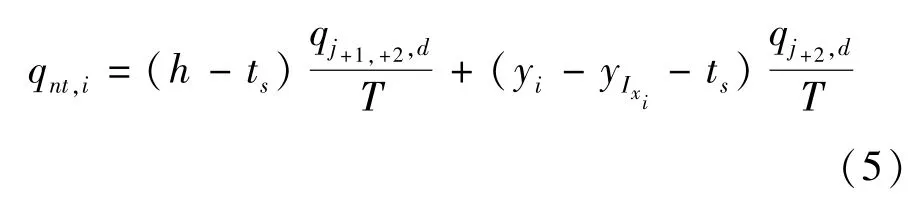
4.1.2 第N+1个时间单元

(1)最后出发列车为j+2列车.

依据假设(3),从图3(b)和表2可以看出,该时间单元开始时刻站台上无乘客滞留,聚集人数为0.随着时间推移,站台非换乘客流聚集人数逐渐增加,最高聚集人数qnt,N+1出现在研究时段结束时刻tT,为该时刻已进入站台的等待出发客流量,聚集时间段为当前时间单元.

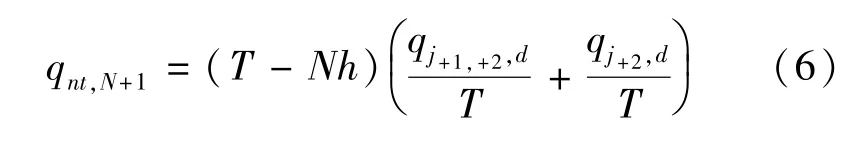
(2)最后出发列车为j+1列车.

从图3(a)和表1可以看出,研究时段结束时刻tT出现在t1时刻之后时,站台非换乘客流聚集人数逐渐增加,最高聚集人数qnt,N+1出现在tT时刻,为该时刻已进入站台的等待出发客流量,包含等待j+1或j+2列车客流、等待j+2列车客流两部分.其中,等待j+1或j+2列车客流的聚集时间段为:当前时间单元;等待j+2列车客流的聚集时间段为:最后j+2列车离站时刻开始,当前时间单元结束时刻tT结束.

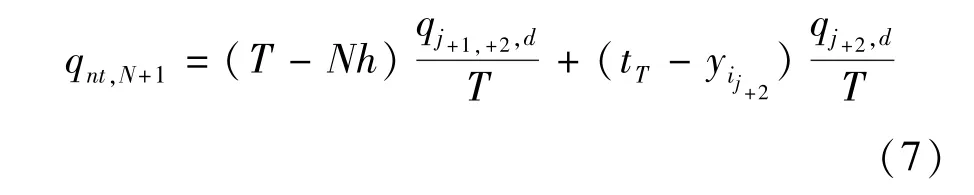
研究时段结束时刻tT出现在t1时刻之前时,tT时刻站台聚集人数小于第N个时间单元内t3时刻站台最高聚集人数,同时tT时刻仍有部分到达目的地的乘客未离开站台,而式(7)并未考虑这部分没有离开站台的客流,导致式(7)计算结果小于tT时刻站台非换乘客流的实际聚集人数.因此,与其他时间单元内最高聚集人数比较时,式(7)计算结果完全可以代替tT时刻站台聚集人数,并不影响研究时段内站台非换乘客流最高聚集人数最终结果.为了避免判断tT时刻与t1时刻之间的先后关系,计算式(7)即可.

4.2 换乘客流聚集人数变化过程

站台换乘客流聚集人数变化过程同样包含前N个、第N+1个时间单元两部分.

4.2.1 前N个时间单元

站台换乘客流的聚集、消散伴随着列车停站时间内乘客的下车、上车发生.依据假设(3)、(6)和图3,任一时间单元内,当前列车分别为运到换乘客流的j+1列车、运走换乘客流的j+2列车时站台换乘客流聚集人数变化过程如图4所示.

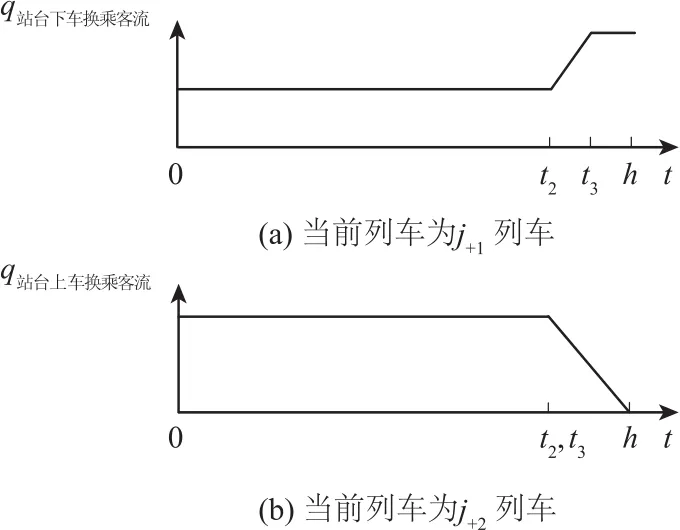
图4 任一时间单元内站台换乘客流聚集人数变化过程Fig.4 Interchange passenger flow assembling change process for time element

(1)当前列车为j+1列车.

从图4(a)可以看出,每一列车到达都有换乘客流下车,增加站台换乘客流聚集人数.站台换乘客流最高聚集人数qt,i持续时间段为:当前时间单元t3时刻开始,当前时间单元结束时刻结束.如图5所示,当前j+1列车为a时,其对应时间单元内站台换乘客流最高聚集人数的聚集时间段ta为:前面j+2列车b的前一j+1列车c对应时间单元的t3时刻(j+1列车c不存在时取换乘站研究时段开始时刻t0)开始,j+1列车a对应时间单元的t3时刻结束.

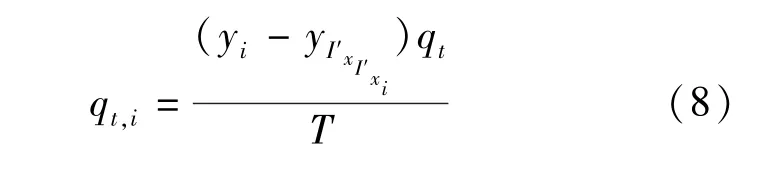
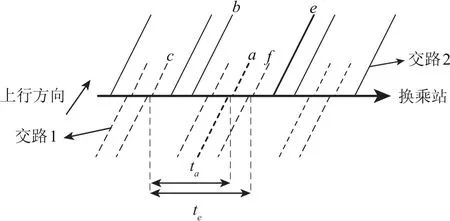
图5 站台换乘客流最高聚集人数聚集时间段分析Fig.5 Maximum interchange passenger flow assembling time

(2)当前列车为j+2列车.

分析假设(3)可知:如图5所示,只有j+1列车f的后续j+2列车e运走换乘客流,j+2列车的后续j+2列车b并不运走换乘客流.从图4(b)可以看出,站台换乘客流最高聚集人数qt,i时刻出现在t2/t3时刻.当前j+2列车为e时,其对应时间单元内站台换乘客流最高聚集人数的聚集时间段te为:前面j+2列车b的前一j+1列车c对应时间单元的t3时刻(j+1列车c不存在时取换乘站研究时段开始时刻t0)开始,前一j+1列车f对应时间单元的t3时刻结束.可以看出,j+2列车e对应时间单元内站台换乘客流最高聚集人数与其前一j+1列车f对应时间单元内站台换乘客流最高聚集人数是相同的.

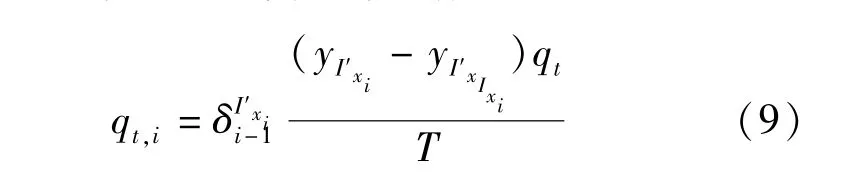
4.2.2 第N+1个时间单元

从图4(b)可以看出,当换乘站最后出发的上行列车是j+2列车时,该列车或其前面的j+2列车运走站台上已聚集换乘客流,站台上不存在换乘客流;从图4(a)可以看出,当最后出发的上行列车是j+1列车时,站台上存在j+1列车运到的换乘客流,站台换乘客流最高聚集人数qt,N+1持续时间为第N +1个时间单元,为第N+1个时间单元开始时刻Nh站台等待出发的换乘客流量.

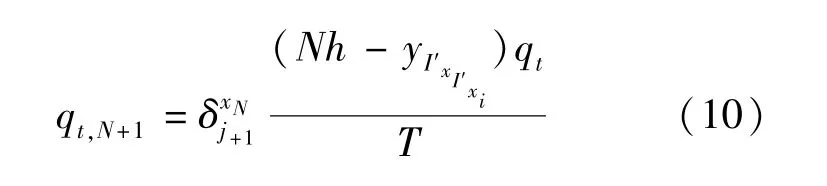
4.3 换乘站台最高聚集人数计算

基于上述分析,上行换乘站台非换乘和换乘客流最高聚集人数的出现时刻如表3所示,可以发现:任一时间单元内站台非换乘和换乘客流的最高聚集人数出现时刻存在交集,交集时刻即是站台最高聚集人数的出现时刻,在交集时刻同步叠加上述两类客流即可得出站台的最高聚集人数.

利用式(4)-式(10),在表3所示的交集时刻同步叠加两类客流,研究时段N+1个时间单元内,上行侧式换乘站台最高聚集人数的计算公式(式11).只要找出这N+1个站台最高聚集人数,最大值即是上行侧式换乘站台最高聚集人数qMAX.

表3 站台非换乘和换乘客流最高聚集人数的出现时刻Table 3 Time of maximum assembling passenger

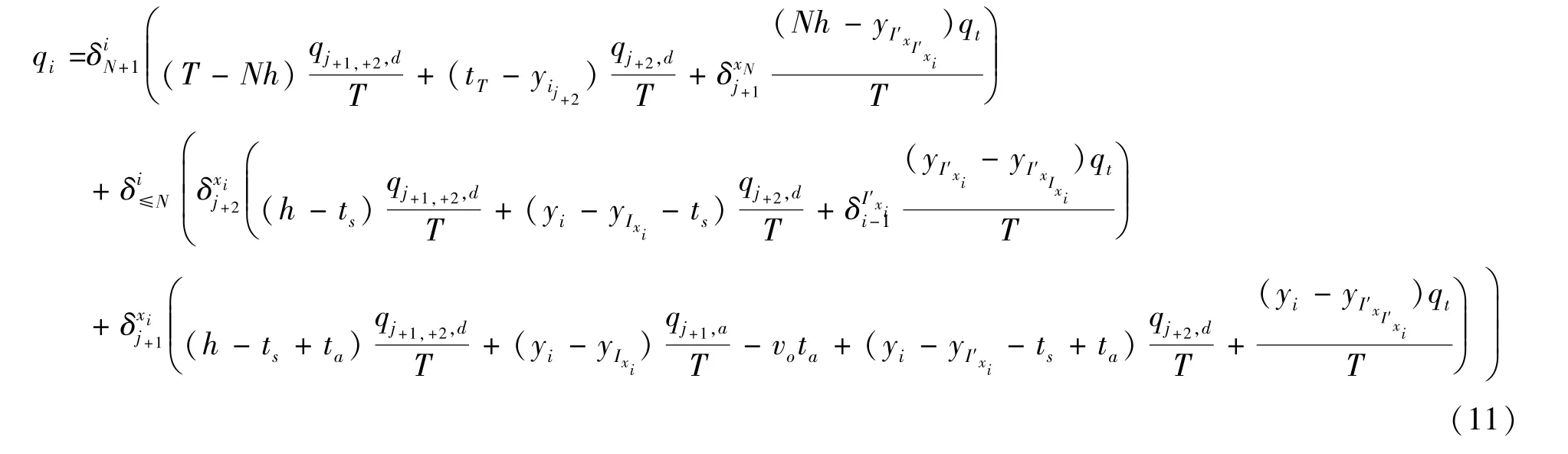
5 算例应用

车站上(下)行列车共用同一站台、不存在支线的某城市轨道交通线路,其衔接交路下上行侧式换乘站台相关参数如表4所示.换乘站出发列车的发车间隔均为2分钟,发车顺序为:j+1、j+2列车交替发车28列,j+1列车发车2列.

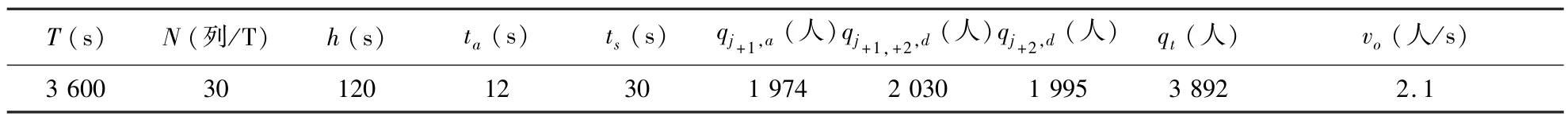
表4 某线路衔接交路下上行侧式换乘站台相关参数Table 4 Parameters of joint routing transfer side-platform

依据式(11),算例换乘站台的最高聚集人数qMAX为610人,出现在研究时段结束时刻tT=3 600 s,各时间单元上行换乘站台最高聚集人数如图6所示.

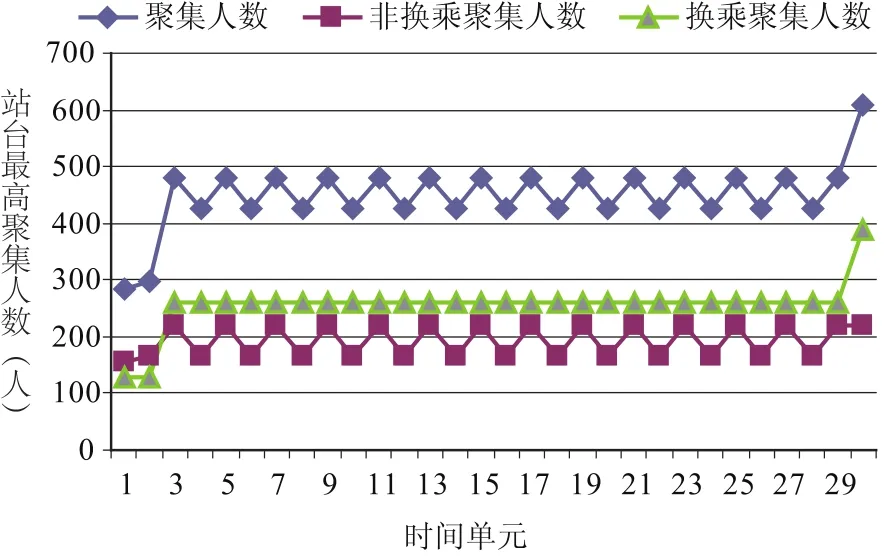
图6 各时间单元上行换乘站台最高聚集人数Fig.6 Maximum interchange passenger for time element

由地铁设计规范的计算方法[5],算例换乘站台的最高聚集人数为330人.

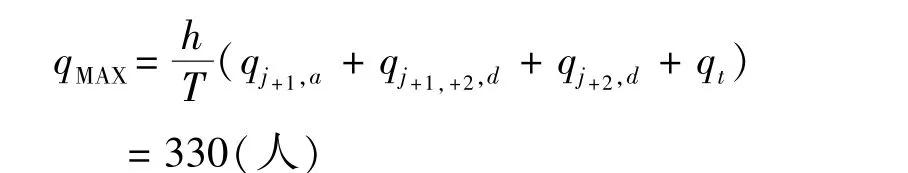
与地铁设计规范相比,本文计算方法所得结果明显偏大,但更符合衔接交路下换乘站台聚集人数的实际变化过程,相对准确.主要原因在于,地铁设计规范的计算方法没有区分换乘站台上j+1列车、j+2列车的运载属性,总体上认为所有列车的发车间隔都是相同的,但该发车间隔一般都小于j+1列车、j+2列车的实际发车间隔,导致其计算结果偏小.

换乘客流占换乘站客流比例对站台最高聚集人数计算结果影响如图7所示,可以看出:换乘客流所占比例越大引起两种计算方法所得结果的差别越大,较大的换乘比例进一步加剧了换乘站台的客流压力,降低了城市轨道交通的服务水平,表明本文研究换乘站台的最高聚集人数十分必要.

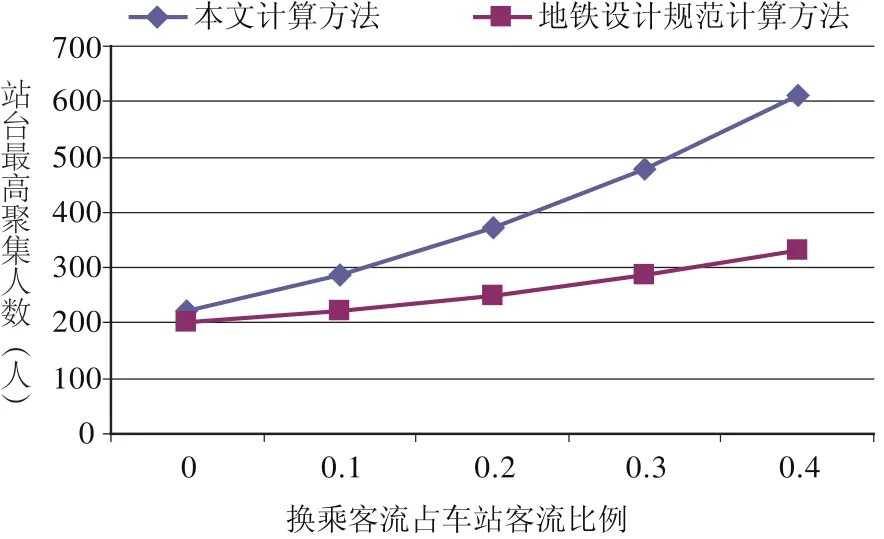
图7 换乘客流占车站客流比例对计算结果影响Fig.7 Results of different interchange passenger ratios

6 研究结论

针对车站上(下)行列车共用同一站台、不存在支线的城市轨道交通线路衔接交路下侧式换乘站台,基于已知的运行图,运用趋势分析法计算某一时段内侧式换乘站台的最高聚集人数.算例应用表明,本文提出的衔接交路下侧式换乘站台最高聚集人数计算公式是可行的;与地铁设计规范相比,本文提出的计算方法所得结果相对准确.

本文基于若干假设条件下,得出衔接交路下侧式换乘站台最高聚集人数计算公式.因此,充分考虑假设条件的合理修正,衔接交路下岛式换乘站台和复合式换乘站台最高聚集人数的计算将是下一步的研究工作.

[1] 毛保华,刘明君,黄荣,等.轨道交通网络化运营组织理论与关键技术[M].北京:科学出版社,2011. [MAO B H,LIU M J,HUANG R,et al.Operational theories and key technologies of rail transit networks [M].Beijing:Science Press,2011.]

[2] Kepaptsoglou K,Karlaftis M G.A model for analyzing metro station platform conditions following a service disruption[C]//201013thInternationalIEEE ConferenceonIntelligentTransportationSystems. Funchal,Maderia Island,Portugal,2010:1789-1794.

[3] 赵宇刚,毛保华,杨远舟,等.城市轨道交通站台最高聚集人数计算方法研究[J].交通运输系统工程与信息,2011,11(2):149-154.[ZHAO Y G,MAO B H, YANG Y Z,et al.Methods of calculating on urban rail the maximum assembling transit platforms[J].Journal of Transportation SystemsEngineeringandInformation Technology,2011,11(2):149-154.]

[4] 赵宇刚.考虑服务水平的城市轨道交通换乘问题研究[D].北京:北京交通大学,2011.[ZHAO Y G.On interchange of urban rail transit considering level of service[D].Beijing:Beijing Jiaotong University,2011.]

[5] GB 50157-2003地铁设计规范[S].北京:中国计划出版社,2003.[GB 50157-2003 Code for design of metro [S].Beijing:China Planning Press,2003.]

Calculating the Maximum Assembling on Transfer Side-platform of Urban Rail Transit

WANG Yong-liang,ZHANG Xing-chen,JIANG Yang,ZHU Yu-ting
(MOE Key Laboratory for Urban Transportation Complex Systems Theory&Technology, Beijing Jiaotong University,Beijing 100044,China)

The maximum assembling of some period on joint routing transfer side-platform of urban rail transit line is calculated by trend analysis.Based on relative hypotheses,interaction of passenger,train and platform in time element is analyzed by trend analysis,in order to understand non-interchange and interchange passenger flow assembling change process;calculation equation of maximum assembling on transfer platform is concluded by synchronous superimposition.The numerical example indicated that calculation equation is feasible of maximum assembling on transfer platform;the final result by the calculation method of this paper is more accurate than by the one of code for design of metro.

urban traffic;maximum assembling;trend analysis;transfer side-platform;joint routing

U231

: A

U231

A

1009-6744(2013)05-0167-08

2013-04-09

2013-06-07录用日期:2013-06-26

国家基础研究计划项目(2012CB725406);国家自然科学基金重点项目(71131001,71201008).

王永亮(1983-),男,山西晋城人,博士生.

*通讯作者:xczhang@bjtu.edu.cn