基于时刻表的地铁时空扩展网络构建方法研究

刘新华,四兵锋,刘剑锋,杜 凯

(1长安大学电子与控制工程学院,西安710064;2北京交通大学,北京100044; 3北京交通发展研究中心,北京100055)

基于时刻表的地铁时空扩展网络构建方法研究

刘新华*,四兵锋2,刘剑锋3,杜 凯1

(1长安大学电子与控制工程学院,西安710064;2北京交通大学,北京100044; 3北京交通发展研究中心,北京100055)

针对城市地铁网络动态客流分配模型构建问题,提出了基于时刻表的地铁时空扩展网络构建方法.首先对地铁网络客流动态特征进行分析,在此基础上构建了基于物理站点和区间的地铁空间网络.结合列车运行时刻表,对物理站点进行时间扩展,定义了基于时刻表的地铁空间扩展网络.最后对物理节点以及物理弧进行扩展,构建了基于时刻表的地铁时空扩展网络,并对网络中的基本元素进行了定义.基于时刻表的地铁时空扩展网络的构建方法,将复杂的地铁客流动态分配问题采用经典的静态用户平衡模型来进行描述,可为城市地铁网络动态客流分配研究提供参考.

城市交通;客流分配;动态;地铁网络;时刻表

1 引 言

地铁网络客流分配问题是把握地铁网络客流时空分布特征的基础,对提高城市地铁运营精细化管理水平具有重要意义.由于地铁车辆运行须严格按照预先设定的时刻表进行,因此基于时刻表的动态配流更适合于城市地铁网络.本文在地铁客流动态特征分析的基础上,基于城市地铁网络的物理拓扑属性,结合地铁列车运行时刻表,采用图论的相关理论及方法,构建了地铁时空扩展网络,并对网络中的基本元素进行了定义和描述,可为城市地铁网络动态客流分配提供参考.

交通流量分配问题最早起源于城市道路网. Wardrop[1]首先提出了道路网络平衡的概念和定义,为道路路网流量分配奠定了基础;随着研究的深入,流量分配问题被引入更加复杂的城市地面公交网,如Chriqui和Robillard[2]基于乘客期望选择总出行时间最短的行为,引入“公交线共线”的概念,共线思想贯穿于后来的公交线网配流研究中; Spiess利用策略的概念来说明公交共线问题,策略由乘客的个人偏好及在出行过程中所获得的信息决定,可以表示为一系列的规则,乘客按照这些规则前往出行终点[3];Nguyen和Pallottino引入了超级路径(hyperpath)的概念[4],利用图论理论来描述乘客的路径选择行为,同时提出了基于用户平衡的公交网络配流模型.

国内学者试着将城市道路交通网络和城市地面公交网络中的一些理论方法应用到城市地铁网络的配流中.例如,Tong[5]研究了随机动态客流分配算法并建立了相应模型;四兵锋等基于随机用户的平衡原则构建了随机均衡配流模型[6].

相对于静态交通分配,动态交通分配的主要特征是把路段阻抗与其流量的二维问题变成了路段阻抗、交通流量以及时间的三维问题.动态的公交网络配流研究需建立一个与时间相关的公交网络,根据Poon等的分析,可以将与时间相关的公交网络分成四类[7]:历时图(Nuzzolo et al)[8],对偶图(Moller-Pedersen)[9],前向的星型网络图(Tong and Wong)[10],时空扩展图(Nguyen等;Hamdouch和Lawphongpanich)[11].其中Hamdouch等[5]提出了时空扩展图的概念,为动态公交网络配流研究提供了基础.

国内外学者提出了很多动态公交配流的模型,鲜有对地铁动态配流的研究,尚未见地铁时空扩展网络构建方面的论述.

2 地铁网络客流动态特征分析

地铁客流的动态特征主要体现在地铁网络结构的动态变化和地铁网络客流需求的动态变化两方面.

2.1 城市地铁网络结构的时变特征

地铁网络拓扑结构是客流分配的基础,地铁网络拓扑结构发生变化的情形主要有:

(1)地铁新线建成通车及旧线改扩建(中间增加站点或两端延伸);

(2)已营运线路设备升级改造或配合新建线路施工造成部分站点短期关闭;

(3)网络中各条地铁线路首末车时间不同及部分线路开行区间车等情况;

(4)重要节假日及大型活动期间,部分站点采取“列车通过不停车”的临时封站措施.

2.2 地铁网络客流需求的时变特征

与城市道路交通网络的O-D需求类似,城市地铁网络的O-D需求具有明显的时效性,即在不同的时间段内,O-D需求的波动较大.例如,在不同的年份、或同一年中的不同月份、同一月份的不同工作日或周末及同一天中的不同时段,城市地铁网络的O-D需求具有明显的波动.图1为北京地铁全网客流在平日和周末随进站时间分布情况.

图1 北京地铁网络客流随进站时间分布图Fig.1 Flow arrival time distribution for Beijing urban subway network

3 地铁线网空间网络构建

3.1 地铁空间网络构成要素

空间网络描述的是地铁线路、站点及换乘的关系,空间网络给出了地铁站点之间及线路之间的空间关系.空间网络可表示为G(N,A,L),其中N表示网络中的地铁站点集合,A表示网络中的地铁运行区间集合,L表示运行线路集合.通常,城市地铁网络的基本构成元素包括:

(1)站点:可分为起始站、中间站、终点站和换乘站,可表示为i,i∈N.

(2)区间:是地铁网络上相邻两个站点(即车站)之间的交通线路,包含所属线路、运输能力、运行时间等特性.区间可表示为站点对,即a=(i,j)∈A,i,j∈N,其中i表示区间的上游站点,j表示区间的下游站点.

(3)运营线路:可表示为站点的序列,即l= (i1,i2,…,in)∈L,i1,i2,…,in∈N,其中i1为始发站,in为终点站.

(4)路径:地铁网络上任意一对O-D站点(即车站)之间的一串连通区间的有序排列叫做这对站点之间的路径.在地铁成网的情况下,一对O-D之间可以有多条路径.路径也可表示为站点的序列,即p=(i1,i2,…,in)∈L,i1,i2,…,in∈N,其中i1为始发站,即O点,in为终点站,即D点.

3.2 网络构成要素关联关系

本文采用关联矩阵来表示地铁网络中不同元素之间的关联关系.

用关联矩阵A表示站点与站点之间的连接关系,矩阵中的元素为

一个站点数为n的地铁网络,站点之间的关联矩阵可表示为

假定网络中各区间均为双向连接,则上述关联矩阵为对称矩阵.

类似地,同样可以用关联矩阵来分别表示站点与区间、站点与线路、区间与线路及O-D对与路径之间的关联关系,本文不再赘述.

4 基于时刻表的地铁空间拓展网络

基于时刻表的空间拓展网络是根据地铁列车时刻表,在原有空间网络的基础上,对物理站点进行时间扩展而形成的一个复杂网络,下面将以北京地铁网络中的一个简单实例来说明这一过程.

假设乘客出行的O点和D点分别为M4线的国图站和M2线的和平门站,换乘站可以为西直门站或宣武门站,得到如图2所示的网络图.

图2 基于时刻表的地铁网络图Fig.2 Urban subway network based on train schedule

在图2中,站点下方标记的时间为首班车到站时间,即M4线首班车5:19到达国图站,M2线首班车5:09到达西直门站.

根据地铁运营部门提供的地铁列车运行图数据,M4线和M2线在首班车发车1 h内的发车间隔为6 min,可得到如表1所示的列车时刻表.

表1 国图站到至平门站的列车时刻表Table 1 Train schedule of Guotu station to Hepingmen station

结合实际调查数据,假设在西直门站换乘M2线的时间为10 min,在宣武门站换乘M2线的时间为5 min.根据图2和表1,可以得出此次乘客出行可以选择的路径如图3所示.

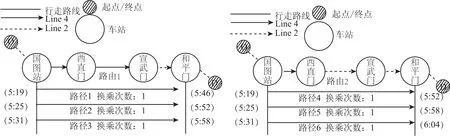
图3 宣武门换乘(左)和西直门站换乘(右)包含的时空路径信息Fig.3 Space-time path information of Xuanwumen(left)and Xizhimen(right)transfer station

在图3中,路径1表示,5:37到达宣武门站,经过5 min的换乘时间于5:42到达M2线站台,等侯2 min后乘坐M2线5:44到达的列车,最后于5:46到达和平门站.路径4中表示乘客5:19同样在国图站乘坐M4线首班车,在西直门站经过10 min的换乘于5:35到达M2线站台,等候4 min后乘坐M2线5:39到达的列车,于5:52到达和平门站.

从上述实例中可以看出,乘客在同样的时间从起点出发,由于选择不同的换乘站,到达终点的时间也不同.在空间拓展网络中,空间网络中所包括的站点、区间、运营线路等要素并未重新定义,只是因为加载了时间轴,路径的定义就会有所改变.

5 地铁时空扩展网络的构建

地铁时空扩展网络是在地铁空间拓展网络的基础上,结合列车运行时刻表信息,对物理节点以及物理弧进行扩展而构建起来的.时空扩展网络构建步骤如下:

(1)将物理节点在时间轴上进行扩展,即对经过该节点的所有线路的所有车次的离站时点分别用扩展节点表示(将列车停站时间包含在运行时间内,因此无需用扩展节点来表示到站时点);

(2)将同一线路的同次列车在相邻物理节点上的离站时点通过列车运行弧连接起来;

(3)将同一物理节点上的不同线路列车的到站时点和离站时点通过换乘弧连接起来.

具体过程如图4所示.

地铁时空扩展网络可表示为G(N,A,L,T),其中N表示网络中的地铁站点集合,A表示网络中的地铁运行区间集合,L表示运行线路集合,T表示所有列车离站时点集合.在地铁时空扩展网络中,包括以下基本构成元素:

(1)时空节点.

时空扩展网络中的每个节点有两个标签.一个标签表示在物理网络中的节点,包括站点名和线路归属两个属性;另一个是时间元素,显示其时间状态.可以用表示物理站点i的时空扩展节点,其中i∈N,l∈L,t∈T,即通过站点i的线路l在t时点的时空节点.

(2)时空弧.

时空扩展网络中包含两种类型的时空弧,即列车运行弧和换乘弧.

(3)时空路径.

在时空扩展网络中,时空路径一般是由运行弧和换乘弧组成的有序排列.一条时空路径不仅满足空间上的连通性,即乘客只有在换乘站点才能实现不同线路之间的换乘;同时也满足时间上的可行性,即乘客在站点i实现从线路l1到线路l2的换乘,那么乘坐线路l1的乘客到达换乘站点i的时点t1加上其换乘时间须小于线路l2的列车到达站点i的时点t2.即

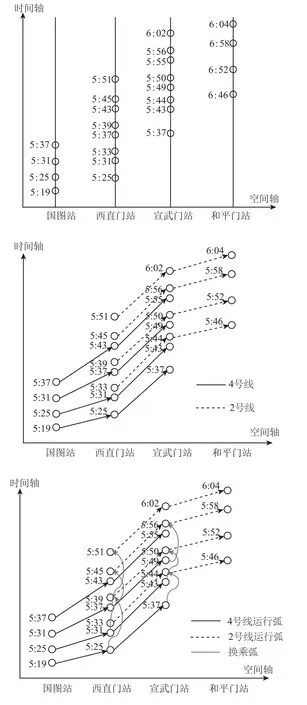
图4 地铁时空扩展网络构建过程实例图Fig.4 Instance of method to build the space-time extended network for urban subway network

在地铁网络化运营条件下,一个O-D对之间可以有多条时空路径.假定乘客从起点到达终点的过程中首先在空间网络中选择一条路径,然后在时空扩展网络中所对应的多条时空路径中再选择一条时空扩展路径.也就是说,当乘客在一条空间路径上从起点到达终点时,他所选择的出发时间和到达时间的不同构成了多条与该路径关联的时空扩展路径.

6 研究结论

由于城市地铁列车基本严格按照时刻表运行,因此,基于时刻表的动态配流方法更适合于城市地铁网络配流.通过地铁时空扩展网络的构建,可以将乘客出行的时空信息转换为路径信息,即乘客出行的空间路径和时间序列都包含在时空网络的时空路径中.这样,复杂的地铁客流动态分配问题就可以采用经典的静态用户平衡模型来进行描述,大大降低了地铁客流动态分配问题的复杂性,增加了其实现性,为下一步构建基于此的路径广义费用模型和基于时刻表的地铁网络客流动态分配模型及求解算法奠定基础.

[1] Wardrop J G.Some theoretical aspects of road traffic research[C].Proceedings of the Institution of CiviI Engineers-part II,1952,36:325-378.

[2] Chriqui C,Robillard P.Common bus lines[J]. Transportation Science,1975,9:115-121.

[3] Spiess H,Florian M.Optimal strategies:a new assignment modelfortransitnetworks[J].Transportation Research-B,1989,23(2):83-102.

[4] Nguyen S,Pallotino S.Equilibrium traffic assignment in large scale transit networks[J].European Journal of Operational Research,1988,37(2):176-186.

[5] Tong C O,Wong S C.A stochastic transit assignment model using a dynamic schedule-based network[J]. Transportation Research,1999,33:107-121.

[6] 四兵锋,毛保华,刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法[J].铁道学报, 2007,29(6):12-18.[SI Bing-feng,MAO Bao-hua, LIU Zhi-li.Passenger flow assignment model for urban railway traffic network under the condition of seamless exchange[J].Joural of China Railway Society, 2007,29(6):12-18.]

[7] Nuzzolo A,Russo F,Crisalli U.A doubly dynamic schedule-based assignment model for transit networks [J].Transportation Science,2001,35(3):268-285.

[8] Moller-Pedersen J.Assignment model for timetablebased systems[C]//Paper from The Association for European Transport Conference held in Cambridge on 1 January 1999.

[9] Tong C O,Wong S C,Poon M H,et al.A schedulebased dynamic transit network model-recent advances and prospective future research[J].Journal of Advanced Transportation,2001,35(2):175-195.

[10] Nguyen S,Pallottino S,Malucelli F.A modeling framework for passenger assignment on a transport network with timetables[J].Transportation Science, 2001,35(3):238-249.

[11] Hamdoucha Y,Lawphongpanich S.Schedule-based transit assignment model with travel strategies and capacity constraints[J].Transportation Research-B, 2008,42(7): 663-684.

Space-time Extended Network Build Based on Train Schedule of Urban Subway Network

LIU Xin-hua1,SI Bing-feng2,LIU Jian-feng3,DU Kai1
(1.School of Electronic&Control Engineering,Chang'an University,Xi'an 710064,China; 2.Beijing Jiaotong University,Beijing 100044,China; 3.Beijing Transportation Research Center,Beijing 100055,China)

Focusing on the dynamic passenger flow assignment for urban subway network,this paper proposes a method to build the space-time extended network for urban subway system based on the schedule information.First,the dynamic characteristics of network flow are analyzed and the definition of the spatial structure for subway network is proposed based on the physical site and interval.Then,this paper presents the space-time extended network as well as the concept of space-time path,by combining the train schedule information.Then,this paper proposes a method to build the space-time extended network for urban subway system with the schedule information.The definition and description of the basic elements in such network are also provided.The proposed methodology provides a way to use classic static user equilibrium model to describe the complex dynamic flow assignment,which can serve as reference for dynamic flow assignment for urban subway network.

urban traffic;flow assignment;dynamic;subway network;schedule

U231+.92

: A

U231+.92

A

1009-6744(2013)05-0179-05

2013-04-10

2013-06-01录用日期:2013-06-06

中国博士后科学基金资助项目(2013M530018);国家高科技研究发展计划(863计划)项目(2011AA110305).

刘新华(1981—),男,江西省南昌市人,工程师,博士生.

*通讯作者:liuxinhua@bjjtw.gov.cn