高速动车组司机乘务交路优化编制方法

符 卓，袁雪莹，车 瑶

(中南大学 交通运输工程学院， 湖南 长沙 410075)

机车(含高速动车组)乘务交路是指机车司机(机车乘务员)担当值乘任务的固定周转区段，即司机从机务段所在站(乘务基地)到折返站(乘务换乘站)之间往返值乘的线路区段。高速动车组司机乘务交路是否合理，直接关系到动车组司机的需要数及其相关作息时间安排。我国高速动车组司机乘务交路的编制由各机务段的技术人员负责。目前仍以“先到先走”的经典启发式方法为主，靠人工凭经验编制，每次都要花费若干天、甚至半个月的时间才能编制完成，编制质量和劳动强度都有待于运用科学的方法并开发相应的计算机辅助编制系统来改善。

高速动车组司机乘务交路的编制，与普速列车的机车司机乘务交路一样，是以值乘的高速动车组的运行区段及其到发点为依据，安排司机的值乘车次、出退勤时间和地点等的计划。其编制步骤为：(1)根据高速动车组的运行区段及其到发点确定乘务片段;(2)根据乘务片段编制乘务交路;(3)根据乘务交路构建乘务交路循环。乘务片段是指司机在退勤休息或间休前连续值乘的“一个单程或立即折返交路”，且图定旅行时间一般不超过4 h。根据乘务片段的时长和是否有可接续的乘务片段，多数情况下，乘务交路由1对“往返”的乘务片段组成(有1次间休)，有时由1个或3个乘务片段组成(相应地，无间休或有2次间休)，是司机一天的工作安排(日计划)。乘务交路循环是司机一个较长时间段里的工作安排，即乘务排班，由依次值乘的若干乘务交路连接组成。

随着我国近年来开行高速列车对数的增多，以及交路区段划分、列车运行速度、乘务作息时间等方面的原因，除了由1对往返的乘务片段组成的传统非立即折返类型乘务交路外，还出现了大量由立即折返(简称立折)类型乘务片段组成的乘务交路，若此时仍采用传统的“先到先走”方法来编制(即先到的“去程”乘务片段优先接续下一个“返程”乘务片段)，则所需要的乘务员数或乘务片段间总接续时间往往不是最少的。

铁路[1-8]、航空[9]及城市公交[10-11]等行业都开展了对乘务交路编制问题的研究。因运输方式和各国运输组织制度的不同，其编制要求也有所差异，难以直接用来解决带立即折返的高速动车组乘务交路编制问题。近年来，国内也有不少学者从事与高速动车组司机乘务交路优化编制相关的研究工作，褚飞跃等[12]研究高速铁路单循环形式乘务排班计划编制问题;王莹等[13]以最小化每天需要的乘务组数量为优化目标，构建了编制客运专线乘务交路的集覆盖模型，并设计了一个求解的分枝定价法;王媛媛等[14]将乘务交路编制问题转化为一类特殊的旅行商问题，并设计一个蚁群算法来求解。但这些研究工作中均未涉及由立即折返的乘务片段组成乘务交路问题。

在构建带立折的高速动车组乘务交路时，有以下3种情况：(1)全部乘务片段均两两相互配对组成乘务交路；(2)存在某些乘务片段，不能与其他任何乘务片段配对形成乘务交路，称其为单乘务片段“交路”，且不安排便乘；(3)由3个以上乘务片段组成乘务交路。文献[15]将带立折的高速动车组乘务交路构建归结为一类集合分解问题来求解，但只能处理第1种情形，在应用中有局限性。

本文在文献[15]的基础上进行拓展，提出一种能同时处理上述3种情形的带立即折返的高速动车组司机乘务交路优化模型及其求解算法，在满足相关约束条件下，使需要的司机数和司机的冗余休息时间为最少。弥补现有方法只考虑非立即折返类型或只能处理上述第1种情形的不足。

1 高速动车组司机乘务交路分析

根据组成乘务交路形式的不同，可将高速动车组司机乘务交路归纳为以下3种类型：

(1) 非立即折返型(也称间休折返型)。指司机从机务段所在站(本段站)出勤，担当去程乘务片段的值乘任务到达司机换乘站(折返站)，按照乘务作业时间标准间休后，再担当返程乘务片段的值乘任务返回本段站，见图1，图1中的Pi为乘务片段(i为乘务片段编号)。普速机车司机乘务交路基本是由该类型的乘务片段组成，只是乘务片段的时长和间休时长与高速动车组司机的有所不同。目前相关文献中涉及的基本上是这种类型。

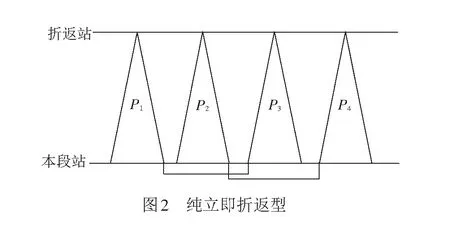
(2) 纯立即折返型。指司机从本段站出勤值乘乘务片段，到达折返站作短暂停留后(一般不超过90 min)立即值乘同一动车组返回本段站，组合成一个总值乘时间不超过4 h的立即折返乘务片段，按照规定间休后继续接续另一立折乘务片段，最终返回本段站退勤，见图2。与类型(1)不同，在这种情形下，每个立折乘务片段没有明确的去程或返程，即当P3为去程乘务片段时，可接续P4；当P3为返程乘务片段时，可被P1接续。

(3) 混合折返型。指在某些乘务交路中，既有立折乘务片段，又有非立折乘务片段，即司机从本段站(或折返站)出勤，担当“去程”乘务片段的值乘任务，间休后再担当“返程”乘务片段的值乘任务到达折返站(或本段站)退勤，见图3。如立折乘务片段Pi可以接续从本段站出发的非立折乘务片段Ri或立折乘务片段Pj(j为乘务片段编号)，也可被从折返站返回的非立折乘务片段Qi接续。

带立折的高速动车组司机乘务交路问题，是随着我国开行高速动车组对数增多、交路区段划分等列车运行组织新要求下出现的新问题。相较非立折乘务交路问题，立折乘务片段的起点站和终点站为同一车站，其乘务交路构建更为复杂，即需考虑其是接续其他乘务片段，还是被其他乘务片段接续。目前各机务段的乘务交路编制人员往往先采用非立折型“先到先走”编制方法构建乘务交路初始方案，再凭经验进行局部调整得出最终方案。编制时间长、难度大，且难以做到整体最优。

2 优化模型构建

2.1 乘务片段接续时间矩阵

每一个非立折乘务片段是去程或返程，具有唯一性。与此不同，一个立折乘务片段既可以作为“去程”从而接续其他乘务片段，也可以作为“返程”而被其他乘务片段接续，不同的接续方案，其乘务片段间的接续时间也不同。

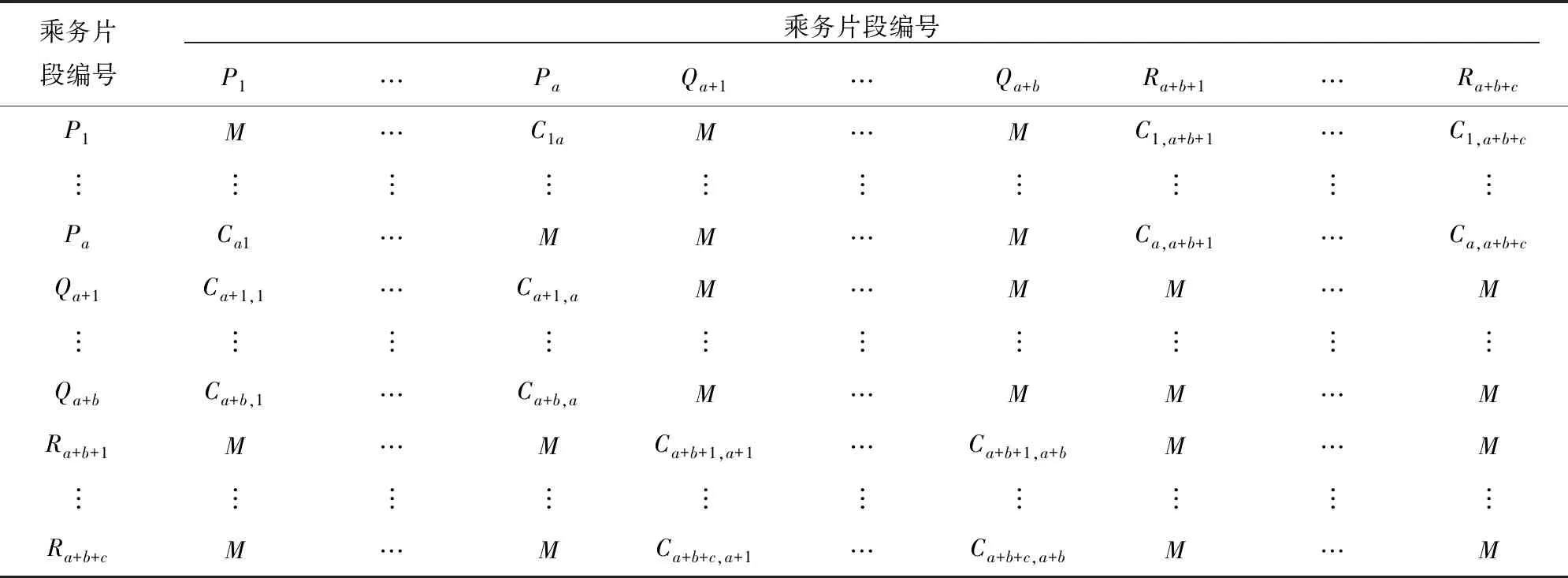
表1 乘务片段接续时间矩阵

为了让司机更好地休息，有时会要求所编排的乘务交路不出现司机连续在折返站过两夜的情形，即从折返站出勤的必须安排在本段站退勤，此时可将从折返站出勤又在折返站退勤的交路接续视为无效接续，也用足够大的正整数M表示其接续时间。

( 1 )

2.2 数学模型

在与乘务交路编制有关的现有文献中，常常将该问题归结为集合覆盖问题(Set Covering Problem)或集合分解问题(Set Partitioning Problem)模型来求解。但这些方法并不适合于本文所讨论的问题类型。于是建立新的双目标0-1整数规划模型为

设

( 2 )

( 3 )

则

( 4 )

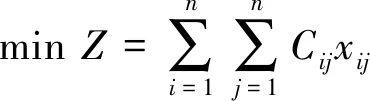
( 5 )

( 6 )

( 7 )

( 8 )

( 9 )

式中：wi为值乘乘务片段i时司机的工作时长；W为日工作时长限制；K为乘务交路数。

一个乘务交路需由一位司机值乘，乘务交路数越少，司机需要数也就越少。设共有n个乘务片段，若所有的乘务交路都是由1个乘务片段单独组成，即各乘务片段间相互不接续，式( 4 )的值为0，则乘务交路数(司机需要数)为n个；若所有的乘务交路都是由1对“往返”的乘务片段组成，即式( 4 )的值为n/2，则乘务交路数(司机需要数)为n/2个。显然，式(4)的取值越大，则表示总的乘务交路数(司机需要数)也就越少。因动车组司机资源紧缺、成本高，铁路部门明确要求将最小化乘务交路数(司机需要数)为首要优化目标。

式( 5 )为次要优化目标，表示乘务片段间的总接续时间最短，使得乘务片段间的接续尽量紧凑，有利于司机退勤后能有更多的时间集中休息。式(6)表示乘务片段i和j最多配对接续一次，求和式为0时表示该乘务片段未能与其他乘务片段配对接续，成为单乘务片段“乘务交路”。因此，乘务片段都能相互配对接续构成乘务交路和部分乘务片段相互间不能配对接续构成乘务交路的两种情形都已被该模型所涵盖，更具通用性。式( 7 )表示乘务片段间的接续必须是可行的，即均为有效接续。式( 8 )表示每个乘务交路中司机的工作时长不能超过给定的日工作时长限制。

该模型是一个多目标优化模型，式( 4 )所表示的优化目标具有优先权，即先优化该目标，再在此基础上优化第二个目标。式( 4 )、式( 5 )也可以转化为如下的单优化目标函数

(10)

式(10)中的第二项表示对乘务片段未配对接续形成乘务交路的惩罚值。显然，乘务片段配对接续形成有效的乘务交路数越多，该惩罚值就越小；当所有的乘务片段都能配对接续形成有效的乘务交路时，惩罚值为0，与式( 4 )、式( 5 )的优化目标是一致的。

3 求解模型的禁忌搜索算法设计

乘务交路编制问题属于NP-难问题[16-17]。计算复杂性理论已经证明，对于NP-难问题，用精确算法求解时，其计算量会随问题规模的增大呈指数增长。特别是对于较大规模的NP-难问题，用精确算法在可接受的时间内求出这类问题的最优解是非常困难的，因此其精确算法在实际应用中具有局限性。从实际应用的角度考虑，一般都是设计启发式算法来求出问题的近优解或最优解。由于乘务交路构建问题的规模往往较大，因此，根据本文问题的特点，设计了一个求解上述模型的禁忌搜索(TS)算法，TS属于亚启发式算法(也称智能优化算法)之一。设计的主要内容如下:

(1) 解的表示 用0和各乘务片段的序号(1,2,…,n)的一种排列表示问题的一组解，每个乘务片段的序号出现且仅出现一次，相邻两个0之间所包含多个非0序号时，表示相应的乘务片段相互接续构成乘务交路；包含1个乘务片段序号则表示该乘务片段需单独值乘。例如解(0 1 3 0 4 5 2 0 … 0 6 0)表示乘务片段1、3和4、5、2分别接续组合为乘务交路，乘务片段6为单乘务片段“乘务交路”，需单独值乘。

(2) 初始解 一般来说，较好的初始解有助于TS算法在解空间内搜寻到的较优最终解。因此，本文选择用传统的“先到先走”方法生成的方案作为初始解。

(3) 邻域结构 为避免过早陷入局部最优，本算法设置了以下4种基于2-交换产生机制的邻域操作来增强TS算法的随机性和多样性，以便能在减少司机需要数和司机冗余间休时间两个方面都能得到更好的改进。每次随机挑选2个乘务片段(下面示例中有下划线者)，再随机挑选其中一种邻域操作对当前解进行变换。邻域操作后，若相邻两个元素都为0，且该新解又是可行解时，则删去其中一个，表示由单乘务片段组成的“乘务交路”减少了，而乘务片段配对接续形成的有效乘务交路增加了，即式( 4 )所示的目标函数得到了改善。

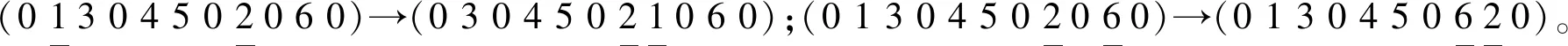
这4种邻域变换分别从不同的角度尝试乘务片段间接续组成乘务交路的不同方案，以便搜索更优的解。其中，邻域变换①、②和④有助于搜索使乘务片段配对组成的乘务交路数增加、或乘务片段接续时间更短的解，优化式( 4 )和式( 5 )所表示的目标函数，邻域变换④中可随机选择是尾部向前或向后插入。邻域变换③主要搜索使乘务片段接续时间更短的解，对式( 5 )进行优化。

(4) 解的评价 由乘务片段的接续时间矩阵[Cij]和上述4种邻域操作中可以看出，当算法搜索进程越接近问题的最优解时，从一个可行解经一次邻域变换操作产生另一个新解也为可行解将越难。为解决此问题，本文将算法设计为接受导致不可行解的变换，即当违反了式(7)的限制条件时，通过在目标函数中增加一个惩罚项而将不可行的程度引入到目标函数中去进行度量(在式(10)中加入第3项)，即

(11)

式中：R为该解中不可行的乘务交路数。p∈[2,20 000] 为惩罚系数， 初始值为100，并进行动态调整：每隔10次迭代测试一次，若前面的10个解都是可行的，则将其除于2；若都是不可行的，则将其乘于2。这样，通过搜索过程中一些不可行解的过渡，有助于找到更好的可行解，降低算法陷入局部最优的可能性。

(5) 算法参数设定 该算法主要有以下参数：

① 禁忌长度。将上述邻域结构中的4种邻域变换作为禁忌对象，禁忌长度在5～10间随机选取。

② 候选解个数。设定为150+2n。

③ 终止准则。算法设定2个参数作为终止准则，即总迭代次数达到12 000+20n，或在3 500+2n次连续迭代步数内当前的最好解没有改变。

(6) 算法框架。本文提出的求解算法可描述如下：

初始化

读入基础数据和各参数的设定值。

按照“先到先走”方法生成的方案作为初始解，并置该解为当前解和当前最好解。

While 算法终止准则未满足 do

While 候选解个数未满足 do

随机挑选2个乘务片段。

随机挑选4种邻域操作之一。

将所挑选的邻域操作对当前解进行变换，并把所产生的新解加入到候选解集中。

End while

从候选解集中按以下顺序找出最佳候选解：①若存在一个优于当前最好解的禁忌候选解，则将其解禁，并作为最佳候选解；②非禁忌候选解中的最佳者；③若所有候选解都被禁忌，则将最佳者解禁，并将其作为最佳候选解。

置新最佳候选解为当前解。

将禁忌表中各禁忌对象的禁忌长度减1，等于0时解禁。

End while

4 算例分析

式( 1 )中Cij值的计算和所提出的TS算法已用Delphi语言进行编程，并在Intel(R) Core(TM)i7-4790、CPU@3.60 GHz、内存8 GB的计算机上实现。本文采用3组实际的高铁动车组数据为例，对模型和算法进行验证。

4.1 算例1

某机务段值乘的部分乘务片段见表2，共73个，不成对，其中有25个是带立折的。若按1个乘务交路最多只能由1对“往返”的乘务片段组成(只有1次间休)来构建乘务交路，则乘务交路数的下限为37。表中的A1、A2为机务段所在站，在该两站到发的、由该机务段值乘的列车可联合编制乘务交路，B为折返站。根据列车出发、到达时刻，间休时间≥90 min，日工作时长≤8 h等规定，可构造乘务片段接续时间矩阵见表3。

表2 高速动车组列车时刻表

表3 带立折的乘务片段接续时间矩阵 min

分别用铁路现场目前常用的“先到先走”方法、本文设计的TS算法、以及Cplex对该算例求解，结果见表4。从表4中可见，用本文设计的TS算法所求出的乘务交路数(任选其中一个见表5)比铁路现场常用的“先到先走”启发式方法编制的要少6个，运算时间基本相等；与Cplex求解结果相同，即求出了问题的最优解，但运算时间只有1 s左右，减少约60倍。由此可见，该TS算法能在较短时间内求出质量较优的解。

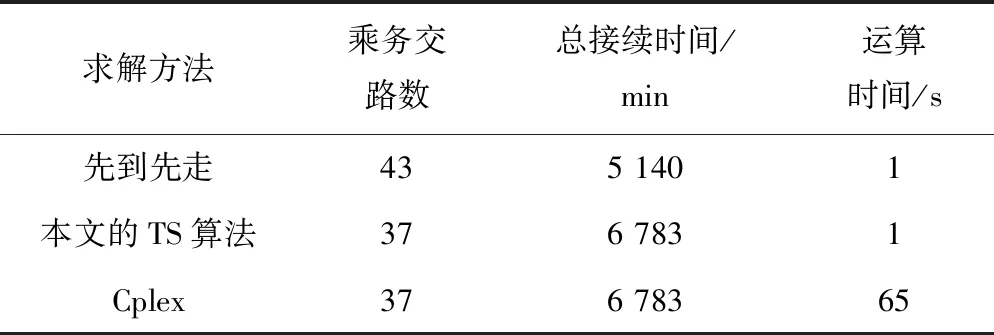
表4 求解结果对比

表5 某机务段高速动车组司机乘务交路优化方案(乘务交路最多由2个乘务片段组成)

表6 高速动车组列车时刻表

续表6 高速动车组列车时刻表

所提出的TS算法收敛情况见图4，其中虚线、实线分别表示乘务交路数(第一优化目标)和接续时间(第二优化目标)的变化情况。需说明的是，第一优化目标是最大化乘务片段配对数，即最小化乘务交路数。开始时乘务交路数等于乘务片段数，每配成1对则乘务片段配对数加1，相应地乘务交路数减1。因此乘务交路数变化趋势是从高到低。单乘务片段“交路”不存在乘务片段之间的接续，本算法中将其接续时间取为0，仅计算相互配对的乘务片段间的接续时间。因此，单乘务片段的“交路”越多，对应的第二个优化目标的值越小。随着第一个目标的优化，单乘务片段“交路”会逐步减少，第二个优化目标值会相应增加，但也是在保证不影响第一个优化目标情况下寻求最小化。

4.2 算例2

某机务段2018年10月30日起值乘的80个乘务片段见表6，其中有26个是立即折返的。由于动车组司机紧缺，且部分乘片段的旅行时较短(约1.5 h)，因此，允许某些乘务交路由3个乘务片段组成(即允许每天有2次间休)，以及个别乘务片段的旅行时间可略超过4 h(最大值是4.8 h)、个别乘务交路的司机日工作时长可超过8 h(最大值是旅行时间10.13 h，加上出退勤辅助时间后是14.6 h)。按照这些要求，现场编制人员人工编制的结果是每天有36个乘务交路，并已按此方案实施；按照同样的限制条件，用本文的TS算法运行约4 s，输出的结果是只需33个乘务交路，可节省3个，其中的一个方案见表7。

表7 高速动车组司机乘务交路优化方案(乘务交路最多由3个乘务片段组成)

4.3 算例3

文献[15]提供了一个有18个乘务片段的算例，并设计了一个蚁群遗传混合算法求解该算例，得到乘务交路数为9个，接续时间为2 658 min，运算时间约40 s。采用本文设计的TS算法对该算例进行求解，得到了同样的优化结果，但运算时间只需约0.1 s。用Cplex例求解也得到了同样的结果。

5 结论

(1) 本文通过对带立折的高速动车组司机乘务交路优化编制问题的分析和归纳，以所需要的动车组司机数和司机的冗余休息时间为最少建立了相应的0—1整数规划模型，该模型可以描述每个乘务交路由1个或多个乘务片段组成的类型。

(2) 针对问题模型属于NP-难问题的特点，设计了一个求解的禁忌搜索算法，并编程在微机上实现。

(3) 以多个机务段值乘的高铁动车组实际数据为例，对模型和算法进行测试，并对求解结果进行对比分析，验证了本文所提出的方法能快速求出符合实际要求的、较优的高速动车组司机乘务交路方案。

以本文所提出的方法为基础开发的系统已通过了行业内专家的技术评审，并正在南昌机务段和福州机务段等进行示范性推广。