铁路技术站进路调度问题优化研究

赵 军，向江海，彭其渊

(1. 西南交通大学 交通运输与物流学院，四川 成都 611756； 2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756)

技术站是铁路货运网络中的重要节点，通常以3～4 h为一个阶段编制阶段计划，主要解决车流推算、调机运用和到发线安排等问题，以此指导日常运输生产工作。其中，车流推算和调机运用常合称为配流问题；以配流方案为输入，制定到发线安排和进路排列计划称为进路调度问题。为确保阶段计划的可行性和有效性，应综合优化配流和进路调度决策，但整个问题非常复杂，更为可行的策略是先解决配流问题，再解决进路调度问题。本文探讨给定配流方案下的技术站进路调度问题，已知车站数据、运行图和配流方案，该问题关键在于同时指派并调度行车和调车作业的进路及其开始时刻，以使得所有作业在时间和空间上无冲突。与常规车站到发线安排相比，技术站进路调度问题优化存在多项决策任务并行、作业间有复杂时空约束等难点。

目前,国外对铁路车站到发线运用和进路排列问题开展许多研究工作，研究方法可大致分类为进路冲突法、资源冲突法和车间调度法，具体见文献[1]。其中，进路冲突法将原问题抽象为冲突图中的最大独立集问题，相关模型包括点装箱模型[2-3]、集合装箱模型[4]和图着色模型[5]。资源冲突法为基于进路冲突的改进方法，同时考虑所有进路对单个资源的占用情况，相关模型包括集合装箱模型[6]、多商品流模型[7]和约束指派模型[8]。车间调度法将原问题转化为作业车间调度问题，其中，车站被视为车间，资源和作业分别被视为车间中的机器和工件，其相关模型主要有约束规划模型[9]、替代图模型[10]和整数规划模型[11]。

同时，国内也对铁路客运站到发线和进路指派问题开展一定研究。陈彦等[12]建立旅客列车过站径路优化的0-1规划模型，并设计基于极大性概念的模拟退火算法。贾文峥等[13]将原问题转换为约束满意问题，并开发包含多项进程的约束规划算法。赵鹏等[14]以到发线运用和咽喉区进路运用均衡为优化目标，构建0-1规划模型，并编制模拟退火算法求解。郭彬等[15]基于作业链研究高铁车站作业计划鲁棒性编制问题，以列车间总冲突系数最小为目标，建立基于列车时空资源占用函数的模型，并设计改进GRASP算法求解。马驷等[16]建立高铁车站进路分配优化模型，并开发进路分配调整的动态优化算法。彭其渊等[17]针对高铁车站到发线运用调整开展研究，建立混合整数线性规划模型，并设计分支定界算法求解。

然而，国内当前鲜有文献研究技术站进路运用问题。史峰等[18]探讨技术站咽喉区进路排列问题，通过分别将咽喉和进路抽象为网络和路径，设计近似求解算法。崔炳谋等[19]研究编组站进路调度问题，将原问题转换为作业车间调度问题，构建0-1非线性规划模型，并设计基于优先权编码的遗传算法。龙建成等[20]针对相同问题，采用无向图描述车场拓扑结构，构建混合整数非线性规划模型，并设计双层模拟退火算法求解。

综上，国内外主要针对铁路客运站到发线和进路指派/调整开展研究，但所提出方法并不完全适用于我国铁路技术站进路安排的实际情况。首先，所研究的调度对象往往只包括列车到发和出入库作业，不包括机车出入段和调机解编作业。其次，所提出的方法普遍未考虑作业间复杂的时空一致性，且往往只被测试于小型和简化的车站或车站的一端咽喉。最后，所建模型往往未考虑除到发线以外的其他资源的占用约束，且资源占用约束大多以进路为最小单位，与以轨道电路区段为单位进行分段解锁的现场实际不符，模型精度有待提高。

鉴于此，本文为铁路技术站进路调度问题开发完整且有效的求解策略。首先通过问题抽象，将原问题转换为约束指派问题。其次，充分考虑作业间的时空一致性以及轨道电路区段和站线的占用约束，构建0-1线性规划模型，并讨论模型的可拓展性和应对不可行的策略。最后，采用实际案例，验证所提出方法的效果和效率。

1 问题描述

本文探讨技术站单个负责列车接发作业的车场(包括到达场、出发场和到发场)在给定计划时段内的进路调度问题。基于车站数据、运行图和配流方案，给定列车到发时刻、列车解编调机及其时刻，该问题在于为计划时段内各项技术作业指派并调度进路及其开始时刻。不同到发车场的进路调度问题大致相同，区别仅在于可使用的调度资源和需考虑的调度对象，以到达场为例，对所研究问题进行描述,到达场示意见图1。根据《车站行车工作细则》规定的车站与区间、车场与机务段以及车场间的分界点，可确定车场的空间范围。车场内的资源主要包括各类站线、道岔、信号机、绝缘节等，其中站线和道岔由绝缘节分割成轨道电路区段(以下简称轨道区段)，站线和轨道区段组合形成进路。进路调度的主要资源为站线和轨道区段，V为所有站线和轨道区段资源的集合，v为索引。其中，站线可为列车或机车作业提供短暂停留和折返场所，包括到发线、机待线、推峰线、牵出线等，P为所有站线的集合，p为索引；U为轨道区段连接各类站线的集合，u为索引。为使各项作业时空无冲突且与其他车场技术作业衔接，技术站到发车场的进路调度不仅需考虑不同作业在时间和空间上的复杂一致性约束，还需满足站线和轨道区段资源的严格占用约束。

到发车场的作业包括行车和调车作业，两者均占用车场资源。为统一建模，引入“工作”、“活动”的概念将两类作业分解为若干过程，重新定义进路调度对象，并借助“进路模式”的概念将原问题转化为一类约束指派问题。同时，由于两类作业存在差异，将从资源占用时间计算、目标权重取值和进路模式生成3个方面进行差异化处理。

1.1 调度对象

1.1.1 工作

定义技术站里列车或机车通过一条或多条进路而完成的特定走行过程为一项“工作”。据此，可将技术站各类列车的技术作业中列车或机车的走行过程分解为若干项工作，见表1。T为工作集合，t为索引。工作可分类为列车和机车工作，列车工作代表与列车接发和改编有关的作业，包括列车接车、列车推峰、列车转线、列车发车工作；机车工作代表与机车站内走行有关的作业，包括机车入段、机车出段、调机连挂和调机解挂工作。

表1 技术作业与工作对应关系

1.1.2 活动

完成一项工作时，列车或机车的走行过程需要占用一条或多条进路，占用进路的数量由车场结构和作业程序决定。为详细描述工作完成过程，定义列车或机车由一条进路的起点持续走行到终点的过程为一项活动，则一项工作可进一步分解为若干项活动。例如，图1中，一列到达列车从进路信号机接入3道，占用1条接车进路，则该列车接车工作只包括1项活动；一台解体调机从推峰线经4道和1条机待线迂回走行至5道连挂一列待解列车，其全程走行占用3条调车进路，则该调机连挂工作由3项活动构成。

At为工作t所有活动的集合，a为索引。若称进路上的第一个资源为起点，最后一个资源为终点，则每项活动a的属性可用五元组(ta,Oa,Da,sa,0,ea,0)表示，其中ta为活动所属工作，Oa为起点集，Da为终点集，sa,0和ea,0分别为活动最早开始和最早结束时刻，其值由运行图和配流方案给定，活动a∈At可描述工作t从起点oa∈Oa走行至终点da∈Da的过程。

活动为列车和机车走行的基本过程，本文以活动作为进路调度对象，进路调度的任务即是为每一项活动指派并调度进路及其开始时刻，并确保各活动的进路时空无冲突，以顺利完成各项工作，进而完成各项技术作业。

1.2 进路模式

进路调度需为调度对象同时指派进路和调度进路开始时刻，为把两项决策合并为一项决策，本文引入以下“进路模式”的概念：

定义工作t中活动a的进路模式b表示活动a的可选进路与时刻的组合，其属性由所属工作tb、所属活动ab、起点ob∈Oa、终点db∈Da、开始时刻sb≥sa,0、结束时刻eb≥ea,0和资源占用链fb构成，记为

(tb,ab,ob,db,sb,eb,fb)

资源占用链fb由1组资源占用组成，含直接占用资源和因敌对进路而间接占用的资源，记为

fb={{vb,i,kb,i}|i=1,…,|fb|}

{vb,i,kb,i}为某个具体的资源占用，包括占用资源名称vb,i∈V及其占用时区kb,i=[lb,i,rb,i]，其中，lb,i和rb,i分别为占用开始和结束时刻。

各进路模式b的资源占用链fb不是现成数据，但可根据车场结构、进路信息、对应活动性质、列车/机车长度、重量及走行性能、车场联锁系统等进行计算[8,20]。显然，构造fb时，通过合理的参数设置，可体现不同行车和调车作业的差异性。

据定义，进路的起终点为站线或分界点，便于建模，规定起点或终点为站线的进路模式始发或终到于其所对应站线的中心，起点或终点是分界点的进路模式始发或终到于分界点。

对于活动a∈At，若由起点集Oa到终点集Da有n条进路，且基于最早开始时刻sa,0或最早结束时刻ea,0有m个开始时刻，则两者组合可生成n×m个进路模式。记活动a∈At生成的所有进路模式的集合为Ba，所有活动的进路模式集合为

B={b:t∈T,a∈At,b∈Ba}

每个进路模式包含进路和开始时刻信息，可把进路调度问题的两项决策合并为一项。

1.3 问题转化

通过以上定义，工作、活动和进路模式三者之间的关系结构见图2，该结构中的所有信息可通过车场拓扑结构、运行图和配流方案等数据提前生成。基于此，若将技术站到发车场里的各项技术作业分解为若干项工作，并把工作进一步分解为几项关联活动，再为各项活动提前生成有限个包含进路和开始时刻信息的进路模式，则可将技术站进路调度问题转化为一类特殊的约束指派问题，即从给定的若干个进路模式中为各个工作的各项活动指派进路模式，以使得所有活动的进路模式时空无冲突，且拟定的目标函数达到最优。

2 数学方法

本节首先将技术站进路调度问题构建为1个0-1线性规划模型。为使所有活动无时空冲突，该模型考虑唯一性、时空一致性、以及轨道区段和站线占用约束。其中，时空一致性约束确保给定活动对在空间上具有一致的起终点，且在时间上满足要求的时间间隔。轨道区段和站线占用约束确保各轨道区段和各站线在同一时间至多能被一列列车或一台机车占用。然后，讨论模型的可拓展性，并设计迭代算法，确保模型找到可行进路调度方案。

2.1 约束条件

2.1.1 唯一性约束

唯一性约束指必须且正好为每项活动指派一个进路模式，即每项活动有且仅有一条进路和一个开始时刻。令xb为0-1指示变量，若将进路模式b指派给其所属活动，则取值为1，否则，取值为0。唯一性约束可表达为

( 1 )

2.1.2 时空一致性约束

在技术站，不同技术作业在空间上有衔接关系，在时间上有先后顺序，且不同作业间存在安全时间间隔，因此不同活动之间存在着紧密的时空联系，称为时空一致性。

引入空间一致性活动对集合

任一活动对(a,a′)∈Q1表示前项活动a的终点需与后项活动a′的起点相同，例如机车入段起点需与其列车到达的终点相同。

类似的，引入时间一致性活动对集合

任一活动对(a,a′)∈Q2表示前项活动a的结束时刻需与后项活动a′的开始时刻满足给定时间间隔σa,a′，例如机车入段只能在对应列车到达后才能开始。

有Q1⊂Q2，基于这两个集合，可灵活描述以下活动对间的时空一致性要求：

① 为避免工作分解导致不可行解，属于同一工作的任意相邻活动对应满足时空一致性约束。为此，对于各个活动数大于1的工作t∈T，|At|>1，令活动对(a,a′)既属于Q1，也属于Q2，其中，a,a′∈At，a≠|At|，且活动a′仅后于活动a。

② 来自于不同工作但对应同一列车的活动间存在时空一致性要求。对于到达列车，集合Q1和Q2包括各列车接车工作的末项活动分别与其对应机车入段工作的首项活动和与其对应列车推峰工作的首项活动、以及各调机连挂工作的末项活动与其对应列车推峰工作的首项活动。对于出发列车，集合Q1和Q2包括各列车转线工作的末项活动分别与其对应调机解挂工作的首项活动和与其对应列车发车工作的首项活动、以及各机车出段工作的末项活动与其对应列车发车工作的首项活动。

③ 属于不同工作但对应同一调机的活动对也具有时间或空间一致性要求。对于解体调机，各列车推峰工作的末项活动与其对应调机的下次连挂工作的首项活动属于集合Q1和Q2。对于编组调机，各调机解挂工作的末项活动与该调机下次转线工作的首项活动属于集合Q2。

④ 为避免运营过程中的潜在冲突，还可要求部分活动对满足时间一致性约束。例如，集合Q2可包括各机车入段工作的首项活动与其对应调机连挂工作的首项活动、以及各调机解挂工作的首项活动与其对应机车出段工作的末项活动。

(1) 空间一致性约束

具有空间一致性的活动对的衔接点为各类站线。对(a,a′)∈Q1，令Ba,d,p为活动a所有终点为站线p∈P的进路模式集合，即Ba,d,p={b∈Ba|db=p}；令Ba′,o,p为活动a′所有起点为站线p∈P的进路模式集合，即Ba′,o,p={b′∈Ba′|ob′=p}；令Pa,a′⊆P为活动a可终到且活动a′可始发的站线集合，即Pa,a′={p∈P|Ba,d,p≠∅,Ba′,o,p≠∅}。基于Pa,a′，通过式(2)限制各站线p∈Pa,a′处可指派的进路模式，可确保空间一致性约束：

∀(a,a′)∈Q1p∈Pa,a′

( 2 )

由式( 1 )可得，式( 2 )左边第一项∑xb和第二项∑xb′同时为1或0，意味着任意活动对(a,a′)∈Q1所获得的两个进路模式b和b′，满足b的终点与b′的起点始终为同一站线p。

(2) 时间一致性约束

为满足作业间的时间间隔要求，对于活动对(a,a′)∈Q2，直观上可对不满足时间间隔要求的两两进路模式进行约束。为使约束更紧凑，这里提出“极大不匹配进路模式集对”的概念对该约束进行建模。对于活动对(a,a′)∈Q2，有如下定义：

① 进路模式b∈Ba与b′∈Ba′称为是不匹配的，当且仅当b′的开始时刻与b的结束时刻之差小于要求的间隔时间，即sb′-eb<σa,a′；否则，称为是匹配的。

② 进路模式集M⊆Ba与N⊆Ba′称为是不匹配的，当且仅当其包含的所有进路模式对(b,b′):b∈M,b′∈N都是不匹配的。

③ 集合M⊆Ba与N⊆Ba′称为是极大不匹配的，当且仅当对所有的b*∈BaM，进路模式集对(M∪{b*},N)至少包含1个匹配进路模式对，且对所有的b′*∈Ba′N，进路模式集对(M,N∪{b′*})也至少包含1个匹配进路模式对。

Step2对Ba按结束时刻升序排序，创建有序列表L；对Ba′按开始时刻升序排序，创建有序列表L′。

Step4令b′*为L′中开始时刻最小的进路模式，M={b∈L|b与b′*不匹配}，更新L:=M。

Step5若L≠∅，则令b*为L中结束时刻最小的进路模式，N′={b′∈L′|b′与b*不匹配}，更新N:=N∪N′，L′:=L′-N′。

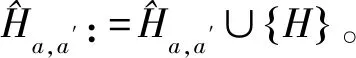
基于此，为满足时间一致性，只需限制各活动对的各极大不匹配进路模式集对H=(M,N)中，最多只能选择1个进路模式

( 3 )

2.1.3 轨道区段占用约束

技术站任一轨道区段同一时间至多被一列列车或一台机车占用，由此，需确保任一轨道区段的所有占用时间区间无交叉，称为轨道区段占用约束。由定义可知，进路模式b占用轨道区段vb,i的时间区间为[lb,i,rb,i]，直观上可对时区有交叉的两两进路模式进行约束，以规避时区交叉情形。本文为加强对该约束的建模，特引入“极大不相容进路模式集”的概念：

(1) 进路模式b∈B与b′∈B称为是不相容的，当且仅当其需在同一时间占用同一轨道区段u，即∃u∈U，vb,i=vb′,i′=u，[lb,i,rb,i]∩[lb′,i′,rb′,i′]≠∅；否则，称为是相容的。

(2) 定义轨道区段u的占用方案Bu为给定B中所有需占用u的进路模式集，即Bu= {b∈B|∃vb,i=u}。称集合Cu⊆Bu在轨道区段u上是不相容的，当且仅当其包含的所有进路模式对(b,b′):b,b′∈Bu,b≠b′都是不相容的。

(3) 称集合Cu⊆Bu在轨道区段u上是极大不相容的，当且仅当对所有的b*∈BuCu，进路模式集Cu∪{b*}至少包含1个相容进路模式对。

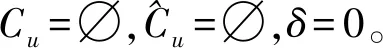
Step2取Bu中所有进路模式的占用结束时刻和开始时刻，创建时刻列表G。其中，各时刻g∈G有一个三元组属性((α(g),β(g),γ(g))，分别表示其时刻值、所属进路模式以及时刻指示标记(若g为结束时刻，则γ(g)为1，否则为0)。

Step3按时刻值对G升序排序，当两时刻值相等时，结束时刻排在开始时刻之前。

Step5令g*为G中取值最小的时刻，若γ(g*)=0，转Step6，否则，转Step7。

Step6更新Cu:=Cu∪{β(g*)}，δ:=1，转Step8。

Step8更新G:=G-{g*}，返回Step4。

( 4 )

2.1.4 站线占用约束

技术站到发车场的站线类型主要包括到发线、机待线、推峰线和牵出线等，与轨道区段相同，各站线同一时间至多被一列列车或一台机车实际占用。但不同的是，任意进路模式只能完整表示其包含轨道区段的占用时区，但不能完整表示其端点处站线的，各站线的占用时区需由开始和结束占用该站线的两项活动共同确定。此外，即使某条站线已被占用，机车仍可从端部进入或离开该站线，但不可穿越该站线，例如，对于到达列车，其本务机车始发于其停留的到发线开始入段工作，其解体调机终到于其停留的到发线结束连挂工作；对于出发列车，其编组调机始发于其所占用的到发线开始解挂工作，其出发机车终到于其所占用的到发线结束出段工作。特规定列车工作必然实际占用其始点或终点处的站线，机车工作在当且仅当通过站线或在站线处停留/折返时才实际占用站线。

引入站线占用活动对集合Q3，各活动对(a,a′)∈Q3表示前项活动a与后项活动a′分别实际开始和结束占用某条站线，由于这两项活动必须按正确的时间顺序终到和始发于相同的站线，因此需要满足时空一致性要求，即Q3⊂Q1⊂Q2。由定义，任意活动对(a,a′)∈Q3中，开始占用活动a必然对应唯一的结束占用活动a′，记为θ(a)。

根据现场实际，集合Q3包括：

(1) 列车接车工作的末项活动与其对应列车推峰工作的首项活动，占用相同到发线。

(2) 各列车转线工作的末项活动与其对应列车发车工作的首项活动，占用相同到发线。

(3) 各列车推峰工作的末项活动与对应调机下次连挂工作的首项活动，占用相同推峰线。

(4) 各活动数大于1的机车工作的各相邻活动对，占用相同到发线或机待线。

任意站线p∈P的三种可行占用情形见图3。可见，第一种情形，若站线p在计划初和计划末均空闲，则其每次占用由1个开始占用活动a和1个结束占用活动a′构成。第二种，若站线p在计划初被占用，则其第1个占用可能只有1个结束活动a′，对此，为了建模方便，可为活动a′引入1个虚拟开始活动a，令其对站线p的占用时区早于计划初时刻，基于此构建1个虚拟活动对(a,a′)并添入集合Q3。第三种，若站线p在计划末被占用，则其最后1个占用可能只有1个开始活动a，类似地，也可为活动a引入1个虚拟结束活动a′，令其对其对站线p的占用时区晚于计划末时刻，创建虚拟活动对(a,a′)并纳入集合Q3。从而，三种站线占用情形可采用统一的方法进行建模。

令Bd,p为实际开始占用站线p∈P的进路模式集合，即Bd,p={b∈Ba|db=p,(a,a′)∈Q3}，Bo,p为实际结束占用站线p∈P的进路模式集合，即Bo,p={b′∈Ba|ob′=p,(a,a′)∈Q3}。一项活动只有在开始占用某条站线时才可能在该条站线处与其他活动冲突，且任意站线在被当前占用活动释放后可立刻由其他活动开始占用，所以，对Bd,p中所有的占用开始时刻引入占用约束足以刻画站线p∈P的占用情况。即对各站线p∈P，为满足占用要求，只需在其各个占用开始时刻lb*,p∈{lb,p:b∈Bd,p}限制占用该站线的活动数不大于1，即

∀p∈Pb*∈Bd,p

( 5 )

由唯一性约束式( 1 )，式( 5 )左边第一项表示在时刻lb*,p前已开始占用站线p的活动数，第二项表示在时刻lb*,p前已结束占用站线p的活动数，两者之差即表示在时刻lb*,p正占用站线p的活动数。

由一致性约束式( 2 )、式( 3 )，任意活动只有在进入站线后才可能离开站线，换言之，任意站线在任意时刻的占用活动数不可能为负数。同时，任意活动对(a,a′)∈Q3中，活动a′的所有进路模式Ba′在站线p上存在一个最晚占用结束时刻τa′,p，即τa′,p=max{rb′,p:b′∈Ba′|ob′=p}。由于活动对(a,a′)∈Q3满足时空一致性约束，若lb*,p≥τa′,p，则活动a终到于站线p的所有进路模式Ba,d,p必包含于{b∈Bd,p|lb,p≤lb*,p}，且活动a′始发于站线p的所有进路模式Ba′,o,p也必包含于{b′∈Bo,p|rb′,p≤lb*,p}，由此，式( 5 )对该活动对恒有∑b∈Ba,d,pxb-∑b′∈Ba′,o,pxb′=0。因此，将式( 5 )改进为

∀p∈Pb*∈Bd,p

( 6 )

2.2 目标函数

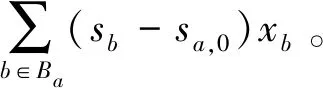
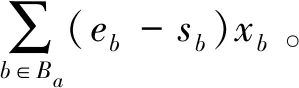
( 7 )

2.3 整体模型与拓展

综上，技术站进路调度问题可构建为以下0-1线性规划模型

M 式( 7 )

s.t. 式( 1 )—式( 4 )和式( 6 )

xb∈{0,1} ∀t∈Ta∈Atb∈Ba

标准模型M具有良好的可拓展性，只需对调度对象和进路模式的生成规则进行简单调整，便可刻画多种运营条件下的进路调度问题，具体如下：

(1) 为描述中转旅客和货物列车，模型M可调整调度工作的内容以及工作间的对应关系。例如，对于各需更换机车的中转列车，可将其抽象为1个列车接车工作和1个列车发车工作，并令其列车接车工作对应1个机车入段工作，其列车发车工作对应1个机车出段工作。对于各只作技术检查的中转列车，只需将其分解为1个列车接车和1个列车发车工作。

(2) 模型M通过调整特殊工作的初始进路模式集，可刻画旅客列车和特种货物列车的股道要求、到发线/推峰线固定使用方案，进路一次/分段解锁等特殊的运营规则。例如，只为旅客列车工作生成端点为邻接站台到发线的进路模式，也只为特种列车工作生成可通往具备接车条件到发线的进路模式；同时，可按照站线固定使用方案为各列车/机车工作生成进路模式集；此外，进路不同的解锁方式可在生成各进路模式的资源占用链时进行刻画。

2.4 迭代算法

为实施标准模型M，需对所有活动按一定的进路选项和开始时刻选项生成进路模式集B。在实际应用时，各活动a的Ba可包含其全部可行的进路选项，因为即使在大型到发车场，对于任意作业一般存在不超过20条可行进路，但是，开始时刻存在无穷多个，Ba只能包含有限个开始时刻选项。由此，基于给定的进路模式集B，标准模型M不一定能获得可行解。为此，鉴于任意可行的进路调度方案必然可为所有活动指派时空无冲突的进路模式，在标准模型M中，将目标函数替换为最大化加权获得进路模式活动的数量，并将唯一性等式约束式( 1 )松弛为不等式，构建技术站进路调度问题的辅助模型为

式( 2 )—式( 4 )、式( 6 )

xb∈{0,1} ∀t∈Ta∈Atb∈Ba

与标准模型相比，辅助模型A不依赖于进路模式集B，总存在可行解，例如，解x={xb=0:t∈T,a∈At,b∈Ba}为可行解。另外，给定进路模式集B下，若辅助模型A的最优解中获得进路模式的活动数不为∑|At|，意味着标准模型M不可行，此时，需为活动提供额外的进路或开始时刻选项来扩充其进路模式，以扩大标准模型可行域的范围。

基于此，提出进路调度迭代算法，反复求解、检验并增广辅助模型A，直到所有活动可在当前进路模式集B下获得时空无冲突的进路模式，主要步骤如下：

Step1对进路模式集B进行初始化。所有活动a均包含其端点间所有可行的进路选项。为尽早给行车作业安排进路，与列车接车和列车发车工作有关的活动a只包含1个开始时刻选项，为其最早开始时刻sa,0；为赋予调车作业更多机动性，基于统一步长ι，与机车入段、机车出段、调机连挂、调机解挂、列车推峰和列车转线工作有关的活动a包含η个开始时刻选项，依次比其最早开始时刻sa,0晚0，ι，… ，(η-1)ι个时间单位。

Step2在每步迭代，基于当前进路模式集B，求解辅助模型A至最优，将获得最优解中进路模式为空的活动视为关键活动。基于统一步长ι，为各关键活动a*扩充κ个开始时刻选项，其值依次比a*的当前最大开始时刻晚ι，2ι，… ，κι个时间单位。基于此，通过遍历给定进路选项和新的开始时刻选项，为a*扩充新的进路模式进入Ba。

Step3Step2迭代执行，直到在当前进路模式集B下，辅助模型A的最优解中获得进路模式的活动数等于∑|At|。此时，使用当前进路模式集B，求解标准模型M，直到获得最优解或者其他预设终止条件达到为止，即可获得最终的进路调度方案。

此外，在初始化和扩充进路模式集B时，为各活动提供了其所有可行进路选项，并从其最早开始时刻起往后逐步增加开始时刻选项。显然，原问题的可行域随着集合B的扩充逐步增大，若各活动的开始时刻选项被赋予的足够多且计算时间允许，所提出算法可找到原问题最优解。当然，为满足阶段计划实时决策的需要，开始时刻选项和计算时间是有限的，但通过合理的参数设置，算法具备找到高质量满意解的能力。

3 算例分析

以某编组站下行到达场的实际数据构造算例，验证所提出方法的有效性。采用Matlab R2016a编程所提出方法，并调用CPLEX 12.8求解标准模型M和辅助模型A。所有计算在CPU为Inter Core i5-4210H 2.9 GHz，内存为12 GB的64位个人计算机上执行。

3.1 算例描述

测试车场采用分段解锁的联锁系统，其拓扑结构见图4。图中，B1和B2为车场与区间的分界点，分别衔接一个接车方向；B3—B8为车场与其他车场/段所的分界点。该车场设置到发线12条，可同时接入B1和B2方向的到达列车，其中A1为正线兼到发线；设置机待线3条，机车折返线1条；驼峰调车采取双推单溜作业方案，设有2条推峰线H1和H2，配有2台解体调机D1和D2；车场内共计轨道区段98个，可排列进路220条(R为进路)，限于篇幅，省略轨道区段和进路详细信息。

考虑测试车场06:00—09:00阶段计划中所有到达解体列车的进路调度任务。假设紧前阶段无作业残留到当前阶段，阶段初解体调机D1和D2分别停留于推峰线H1和H2上。阶段内共有15列到达解体列车，所有到达列车的技术作业按以下办法进行参数设置：各到达列车的解体调机和解体开始时刻按先到先解原则确定，到达作业时间标准为30 min，解体作业时间标准为20 min，两相邻到达列车的解体结束间隔不小于8 min；列车长度为650 m，机车和调机长度为25 m，列车进站速度为30 km/h，机车入段和调机连挂速度为20 km/h，调机推峰速度为8 km/h。基于此，到达列车对应技术作业信息见表2，其中，第6～9列为各项工作的活动编号。

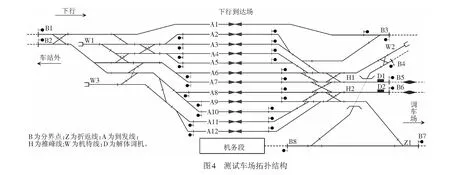
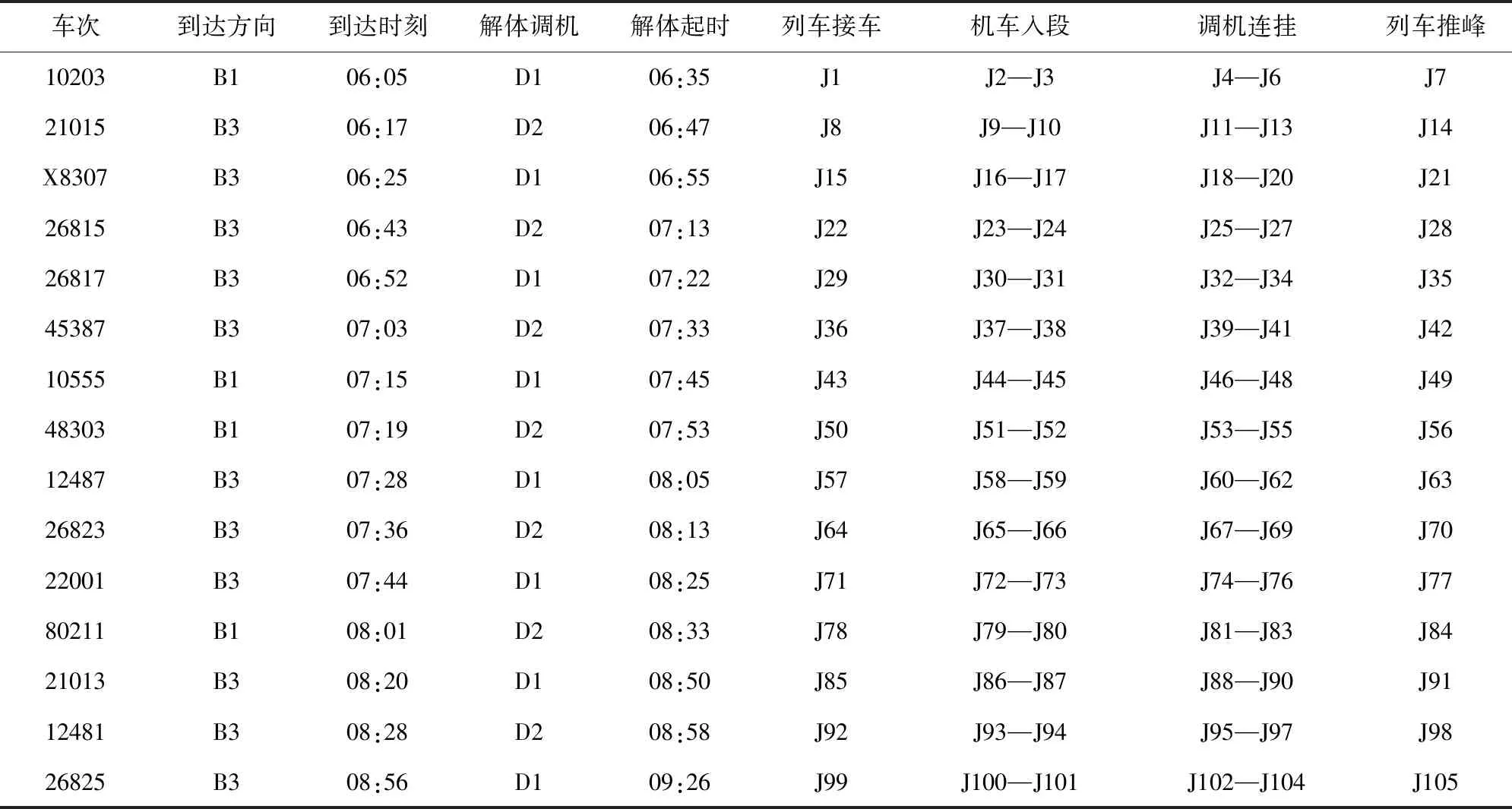
表2 到达列车对应技术作业信息

测试算例共计60项工作和105项活动，各项活动的最早开始和最早结束时刻(sa,0和ea,0)按以下方法确定。列车接车工作唯一活动的ea,0取为到达时刻、sa,0取为到达时刻-可行进路最长走行时间。机车入段工作含2项活动，首项活动的sa,0取为到达时刻+3 min(试风和摘机车时间)，ea,0取为sa,0+最短走行时间；剩余活动的sa,0取为ea-1,0，ea,0取为sa,0+最短走行时间。调机连挂工作含3项活动，首项活动的sa,0取为解体开始时刻、ea,0取为sa,0+最短走行时间；剩余活动的sa,0取为ea-1,0，ea,0取为sa,0+最短走行时间。列车推峰工作唯一活动的sa,0取为对应调机连挂工作末项活动的et′,a,0+2 min(挂机车时间)、ea,0取为sa,0+最短走行时间。

令列车和机车活动的权重分别为10和1，正线和其余站线的权重分别为2和1。时间单位设为min，在初始化所有活动的进路模式时，步长ι取为1 min，个数η取为10。在扩充关键活动的进路模式时，个数κ取为5。

3.2 约束建模技术比较

如2.1.2节所述，对于时间一致性约束，一种直观的建模方法为引入两两关联不等式约束，规避同时选择任意活动对任意两个不匹配的进路模式。另一种可行的建模方法为采用本文提出的极大关联不等式约束(3)，基于极大不匹配的概念将两两不匹配的进路模式最大可能地集计在同一个约束里。类似地，轨道区段占用约束既可直观地采用两两关联技术建模，也可采用本文提出的极大关联不等式约束(4)建模。

两类约束建模技术的比较结果见表3。其中，NTO为约束总数，NMI、NAV和NMA分别为各活动对或各轨道区段约束数的最小值、平均值和最大值；SMI、SAV和SMA分别为各约束涉及变量数的最小值、平均值和最大值。由表可得，对于时间一致性约束，极大关联技术将原只含2个变量的弱约束加强为平均含190个变量的强约束，使得约束总数从115万个减少到649个，减小4个数量级。对于轨道区段占用约束，极大关联技术通过引入平均含38个变量的强约束将原721万余个约束缩减至6 275个，减小3个数量级。因此，相比于两两关联技术，所提出的极大关联技术可显著缩减模型规模，并有利于提高模型求解效率。

表3 约束建模技术比较

3.3 计算结果

测试算例求解过程如下：首先，基于给定技术作业信息和参数设置，为60项工作的105项活动生成初始进路模式16 749个；其次，通过求解辅助模型A一次，验证标准模型M在初始进路模式下可行；接着，基于初始进路模式，求解标准模型M到最优。最终，耗时48.9 s，得到解，总偏移时间为21 min，其中总列车和总机车偏移时间分别为3、18 min；总走行时间为444 min，其中总列车、总机车走行时间分别为197、247 min，总列车、总机车绕行率分别为3.1%、2.9%(绕行率=实际走行时间/最短走行时间-1)。为评估获得解的质量，分别设置η为20、30，重新运行算法。结果分别耗时169.8、191.2 s，得到相同最优目标值。因此，可认定该解是测试算例的最优解，后续计算分析中，参数η取10。

进度调度方案主要信息见表4，表中，DT，TT和DR分别指偏移时间、走行时间和走行绕行率。由表4可看出，求解质量方面，此方案总偏移时间小，有利于实现阶段计划，具体只有8项机车入段活动共延迟9 min，有9项调机连挂活动共延迟9 min，有3项列车推峰活动共延迟3 min，除这些活动以外，其余活动均按最早开始时刻进行。同时，此方案绕行率较低，几乎所有的列车和机车活动获得走行时间最短的进路，有利于节省运营成本。关于计算时间，尽管同时提前生成进路和时刻选项可能增大模型规模，但所提出的方法耗时不到50 s便完成整个求解过程。综上，本文方法具有较好的求解效果和效率，可满足现场实时决策的需要。

表4 进度调度方案

主要资源占用见图5，图5中，横坐标表示时间，纵坐标表示资源，标记“③混合占用”指列车和机车活动共同完成一次实际占用，如列车推峰末项活动与调机连挂首项活动完成对推峰线的占用。资源占用统计见表5，其中，资源利用程度=占用时间/阶段计划长度×100%。可见，站线占用方面，对于到发线，正线A1未被占用，处于下部的到发线利用程度较高，总的来看，到发线能力不紧张，部分到发线常处于空闲状态，说明在研究阶段内到发线接车能力充足。对于推峰线，H1占用次数比H2多1次，且被占用的时间更长，总体上推峰线作业紧凑、能力较为紧张，驼峰能力可能限制研究车场能力的发挥。机待线和折返线中，因调机连挂主要在W3处折返，W3比W1繁忙，同时，W2和Z1被机车因折返入段占用的时间相当。对于轨道区段占用，各轨道区段占用次数和占用时间差距较大，其中，轨道区段114-162DG、138DG、130-136DG、142-154DG和141-161DG最为繁忙，利用程度最高的轨道区段(114-162DG)位于咽喉区的关键部位，是限制研究车场能力的瓶颈。

表5 资源占用统计

3.4 灵敏度分析

3.4.1 站线指派策略的影响

为评估不同站线指派策略的影响，设计三种比较策略。第一种称为动态策略(DTA)，该策略完全根据所提出方法获得的解为各项活动指派站线。第二种称为静态策略1(STA1)，该策略固定推峰线使用，规定解体调机D1和D2分别只能在H1和H2上进行推峰作业。第三种策略在STA1的基础上，进一步固定到发线和机待线的使用，规定从B1方向来的到达列车只能接入A2、A3、A4和A6，从B2方向来的到达列车只能接入A6、A7、A8、A9、A10和A12，机车走行线限定为A5和A11，记为静态策略2(STA2)。

站线指派策略比较结果见表6，其中，第2列和第3列分别为标准模型M的变量数和约束数，第4列为辅助模型A的迭代次数，TDT、TTDT和TEDT分别为总偏移时间、总列车偏移时间和总机车偏移时间，TTT、TTTT和TETT分别为总走行时间、总列车走行时间和总机车走行时间，TTDR和TEDR分别为总列车和总机车绕行率，最后1列为总的求解时间。可知，相比于DTA，STA1固定推峰线使用，使得偏移时间增加3 min，解的质量略差，但变量数和约束数更少，求解速度更快。STA2在STA1基础上进一步固定到发线和机走线使用，其解的质量明显下降，相比于DTA，总偏移时间增加55 min，将加大对阶段计划的影响，但另一方面STA2的变量数和约束数大为下降，求解时间显著缩短。综上，站线使用方案越固定，模型的变量数和约束数越少，求解速度更快，但解的质量变差。因此，在实际应用时，可根据现场情况合理制定站线使用方案，以兼顾进度调度方案的质量和编制速度。

表6 站线指派策略的比较

3.4.2 进路解锁方式的影响

根据现场联锁系统，进路解锁方式包括分段解锁和一次解锁两种。在分段解锁下，列车或机车尾部只要出清某轨道区段后即可释放对该轨道区段的占用。而在一次解锁下，列车或机车尾部只有在出清整个进路后才能一次释放该进路上的所有轨道区段。显然，一次解锁下技术作业对资源的占用时间比分段解锁下的更长，从而对模型的规模和解的质量有影响。

进路解锁方式比较结果见表7。由表7可见，两种解锁方式下，模型规模相当，且都能在较短时间内获得进路调度方案。但相比于分段解锁，一次解锁的总偏移时间增加11 min，总走行时间减少1 min，解的质量更差，说明分段解锁更有利于为活动尽早安排进路，从而减少偏移时间。因此，技术经济条件允许的到发车场应装备分段解锁的联锁系统，以确保车场的能力。

表7 进路解锁方式的比较

4 结束语

本文通过引入工作和活动定义调度对象，利用进路模式表达决策变量，将原包含两项决策任务的技术站进路调度问题转化为只包含一项决策任务的约束指派问题。以总加权偏移和走行时间最小为目标，构建包含唯一性、时空一致性和资源占用约束的0-1线性规划模型。接着，提出标准模型的拓展方法，以描述更多的运营和安全要求，并通过构建辅助模型，设计迭代算法，解决标准模型可能存在的不可行问题。最后，对实际算例的计算结果表明，所提出的进路调度方法具有较好的求解效果和高效的求解效率，可为解决技术站阶段计划优化编制问题提供决策支持。

本文研究可在以下几方面进行拓展。首先，所提出的方法未考虑站线占用的均衡性，下一步可将均衡性目标或要求纳入进路调度问题，增强模型的优化能力。其次，本文尝试提出通用的进路调度描述范式和求解框架，但不同类型车站或车场的特点和复杂性不同，接下来可将所提出方法应用于更多类型的车站和车场，根据研究对象的特点对方法进行相应改进，扩大方法的适用范围。另外，配流和进路调度是技术站阶段计划编制的两个关键问题，相互影响，研究配流与进路调度综合优化、实现技术站阶段计划整体编制也是未来的研究方向。