铁路斜拉桥钢混结合段的收缩徐变行为分析

姚亚东，么超逸，杨永清

(1. 内蒙古大学 交通学院，内蒙古 呼和浩特 010020； 2. 中交公路规划设计院有限公司， 北京 100088；3. 西南交通大学 土木工程学院，四川 成都 610031)

连接钢结构梁段和混凝土梁段的钢混结合段是混合梁斜拉桥的关键构造和薄弱部位。诸多学者一直致力于钢混结合段构造形式和受力行为的研究。20世纪80年代，日本学者对生口桥钢混结合段的构造形式和受力性能开展了研究[1]。1997年，文献[2]通过模型试验研究了汕头礐石大桥钢混结合段的传力机制和应力分布，为钢混结合段的优化设计提供了科学依据。2006年蒋永红[3]研究了混合梁斜拉桥结合段的刚度等效问题。此外，文献[4-8]均对特定桥梁的钢混结合段传力机制和承载能力进行了数值分析和模型试验。然而，上述研究主要针对短期荷载作用下公路混合梁斜拉桥的受力性能及传力机制问题，对铁路混合梁斜拉桥钢混结合段在长期荷载作用下收缩徐变行为的研究甚少。由于铁路混合梁斜拉桥设计荷载更大，结构构造更为复杂，钢混结合段的素混凝土体积庞大、湿交换较少，且处于空间应力状态；同时相关研究也表明收缩徐变作用对钢混结合段受力、变形造成的危害较为显著[9]，因此迫切需要对钢混结合段的收缩徐变行为进行专门研究，以期为相似工程提供理论依据和数据支撑。

本文以亚洲最大跨径的铁路钢箱混合梁斜拉桥——甬江特大桥钢混结合段为研究对象，首先提出了衡量钢混结合段传力性能的指标，基于“朱氏预测模型”[10]和弹性徐变理论，递推出考虑徐变的混凝土本构关系；最后基于Fortran语言对Ansys软件二次开发，深入研究收缩徐变对钢混结合段力学行为的影响。

1 传力指标

文献[11]中绘制了钢混结合段混凝土和钢壳体分担轴力的比例，见图1(a),图1(a)中横坐标为各测试截面距标准钢箱梁侧刚度过渡段起始截面(0 m处)的距离。5 m处为后承压板断面，0～5 m为钢箱梁段，5～12.35 m为钢混结合段,见图1(b)；纵坐标为混凝土、钢壳体分担轴力的百分比。

为更好地衡量钢混结合段的传力状况，图1中传力指标的定义如下：

(1) 后承压板传力率δh:为后承压板和混凝土梁段间接触传递的轴力Ph与截面总轴力P0的比值，即

( 1 )

(2) 钢混结合段传力斜率α：由文献[9]的试验结果可知，钢混结合段端部剪力连接件传力作用显著，中部区域剪力连接件作用较弱。为了清晰认识钢混结合段各排剪力连接件的传力状况，沿纵桥向按一定的比例将其划分成n段，每节段的长度为S。将第n段剪力连接件传递轴力占截面总轴力的比例与节段长度S之比定义为第n段的传力斜率αn，即

( 2 )

同时为深入剖析钢混结合段剪力连接件的传力性能，引入平均传力斜率α、最大传力斜率αmax，分别见

( 3 )

αmax=max{α1，α2,α3，…，αn}

( 4 )

(3) 钢混结合段传力不均匀度δ：通过引入数学中方差的概念来定义传力不均匀度δ，以此来考察钢混结合段中剪力连接件传力的不均匀性及偏离程度，见式( 5 )

δ=

( 5 )

2 收缩的计算

收缩应变与应力历程无关，可通过施加温度荷载来模拟收缩作用。本文根据规范CEB-FIP[12]收缩模型计算获得钢混结合段核心混凝土的收缩应变ε=-112×10-6，由ΔT=ε/aT可知，欲产生上述收缩应变需施加的温度荷载ΔT为-11.2 ℃，其中aT为混凝土的线膨胀系数。

3 徐变理论及本构模型的建立

徐变应变与应力历程相关，对计算式为

( 6 )

式中：ε(t)为t时刻的应变；σ(t0)为t0时刻的应力；E(t0)为t0时刻的弹性模量；C(t,t0)为加载龄期t0的混凝土在t时刻的徐变度。

对式( 6 )变形可知，混凝土总应变可分解为弹性应变εe(t)和徐变应变εc(t)，即

ε(t)=εe(t)+εc(t)

( 7 )

式中：

( 8 )

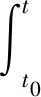
( 9 )

将连续的作用时间划分为Δt1，Δt2，Δt3，…,Δtn等一系列时段，当Δtn充分小时，利用积分中值定理可计算每个时段的弹性应变增量和徐变应变增量，分别为

(10)

(11)

徐变过程中应力变化过程见图2，各时刻的应力可看作该时刻前各时刻应力增量的叠加。其中，tn、tn+1时刻的徐变应变为

εc(tn)=C(tn,t0)Δσ0+C(tn,t1-0.5)Δσ1+…+

C(tn,tn-1-0.5)Δσn-1+C(tn,tn-0.5)Δσn

(12)

εc(tn+1)=C(tn+1,t0)Δσ0+C(tn+1,t1-0.5)Δσ1+…+

C(tn+1,tn-1-0.5)Δσn-1+C(tn+1,tn-0.5)Δσn+

C(tn+1,tn+1-0.5)Δσn+1

(13)

将式(13)与式(12)联立，可得

[C(tn+1,t1-0.5)-C(tn,t1-0.5)]Δσ1+…+

[C(tn+1,tn-1-0.5)-C(tn,tn-1-0.5)]Δσn-1+

[C(tn+1,tn-0.5)-C(tn,tn-0.5)]Δσn+

C(tn+1,tn+1-0.5)Δσn+1

(14)

考虑式(14)的特点，选取指数函数型的朱氏徐变度公式，即

C(t,t0)=∑φj(t0)[1-e-rj(t-t0)]

(15)

式中：φj(t0)为与龄期t0相关的函数，可根据徐变试验获得。

本文采用文献[10]中的推荐公式

将式(15)代入式(14)，可得

C(tn+1,tn+1-0.5)Δσn+1

(16)

式中：

ωj,n+1=Δσ0φj(t0)e-rj(tn-t0)+

Δσ1φj(t1-0.5)e-rj(tn-t1-0.5)+…+

Δσn-1φj(tn-1-0.5)e-rj(tn-tn-1-0.5)+

Δσnφj(tn-0.5)e-rj(tn-tn-0.5)=

ωj,ne-rjΔtn+Δσnφj(tn-0.5)e-0.5rjΔtn

(17)

ωj,1=Δσ0φj(t0)

(18)

(19)

将(16)应用到复杂应力状态，可得

(20)

由式(11)可知

(21)

式中：B为弹性泊松比影响矩阵。

将式(20)代入式(21)，可得

Δσn=E(tn-0.5)B-1(Δεn-ηn-qnAΔσn)

(22)

由式(22)变形，可得

Δσn=

{I+E(tn-0.5)B-1Aqn}-1B-1E(tn-0.5)(Δεn-ηn)=

{B+E(tn-0.5)Aqn}-1E(tn-0.5)(Δεn-ηn)

(23)

式(23)为考虑徐变特性的混凝土本构关系。将此映射关系施加到Ansys分析模型中，就能对钢混结合段核心混凝土的徐变作用进行计算。

4 Ansys二次开发及模型的建立

UPFS是Ansys软件常见的二次开发工具，具有用户可编程的属性。用户可运用Fortran语言对Ansys子程序重新编译，生成满足用户需要的特定版本。本文对Ansys子程序(USERMAT.F模块)进行编译，开发出具有徐变特性的新材料，来实现混凝土徐变作用的计算。Ansys二次开发的流程见图3。

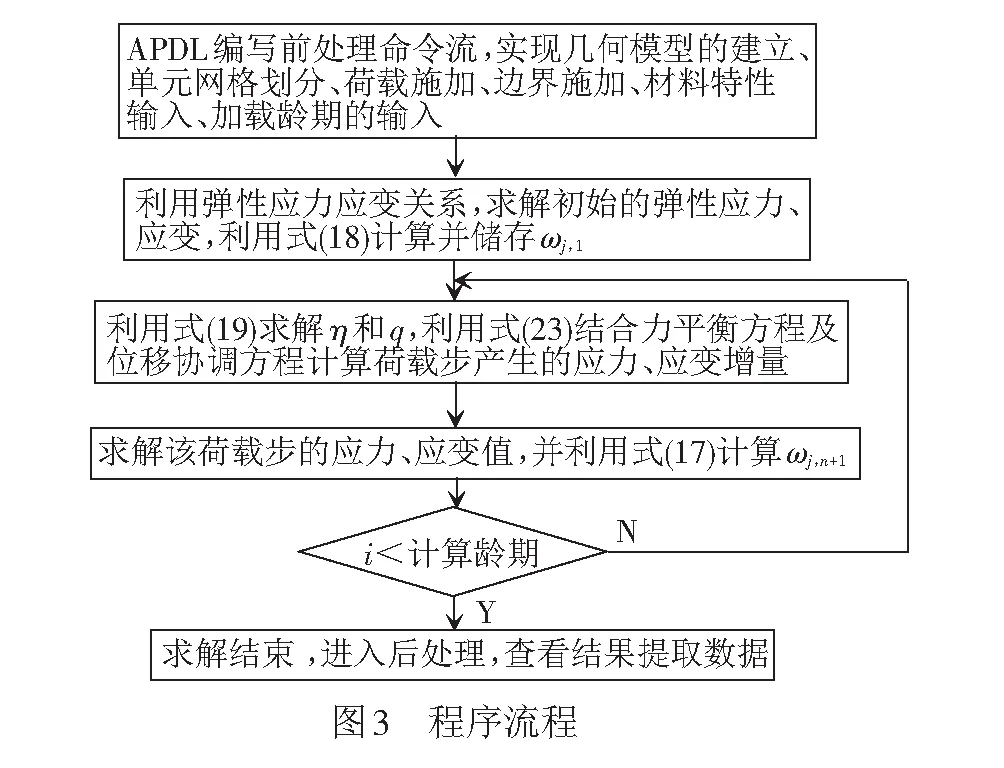
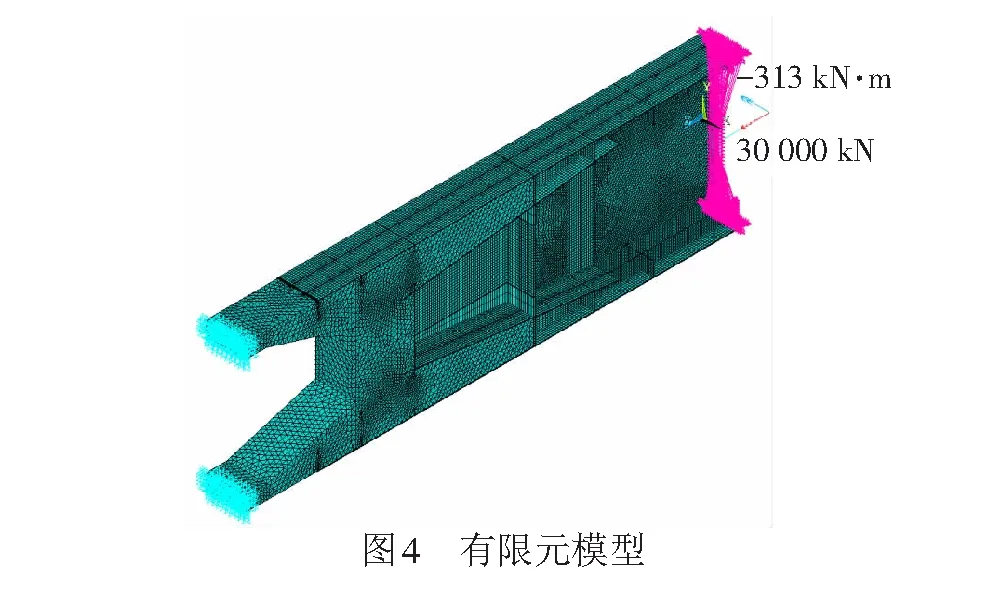
基于二次开发后的Ansys软件建立钢混结合段非线性局部有限元模型，采用三维实体单元Solid65模拟混凝土，通过体积配筋率考虑混凝土的配筋；采用实体单元Solid45、非线性弹簧单元Combin39模拟钢壳体和剪力连接件。通过接触单元用Targe170单元和Conta174单元分别模拟钢壳体内表面和混凝土外表面，两者摩擦系数取0.2，渗透系数取0.1。混凝土选用新开发的材料本构关系；钢壳体及连接件采用双线性理想弹塑性本构模型，弹性模量为210 GPa，屈服应力为320 MPa。模型为悬臂状态，混凝土梁端固定。由圣维南原理及计算结果知，至钢混结合段处力已完成扩散，局部强度满足要求。模型中预应力钢筋采用Link8单元模拟，各节点与混凝土节点耦合，通过降温的方式施加预应力。刚度过渡端面通过Cerig命令形成刚性区后外接梁单元，第1荷载步在梁单元端部以节点集中荷载的形式分100个子步施加，最大轴向荷载为30 000 kN，弯矩为-313 kN·m；第2荷载步施加徐变荷载，徐变时间为3 650 d，分365个子步施加。有限元模型见图4。

5 收缩徐变对钢混结合段受力的影响

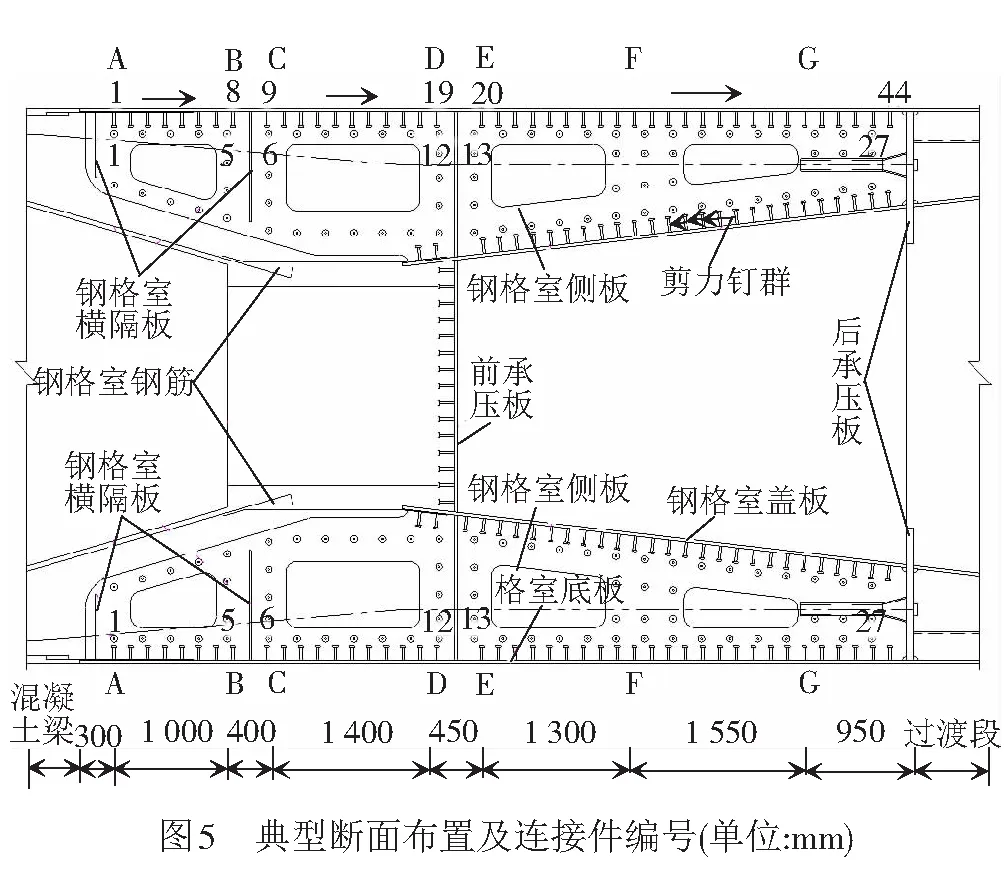
由文献[9]可知，在钢混结合断面最大负弯矩工况作用下钢混结合段受力最不利，因此本文只研究此工况下收缩对钢混结合段应力分布和传力机制的影响。计算徐变时，仅考虑加载龄期7 d恒载工况作用下的瞬时效应与10年徐变效应，对比分析混凝土长期徐变作用对钢混结合段的影响。钢混结合段典型断面布置及剪力连接件编号见图5。

5.1 收缩对钢混结合段受力的影响

绘制最大负弯矩工况下预应力、外荷载、收缩共同作用下钢混结合段各典型测点断面的纵向平均正应力图，见图6、图7。图6、图7数值中负值为压应力，正值为拉应力。1.0F表示预应力、外荷载共同作用的结果；S1.0F表示预应力、外荷载、收缩共同作用的结果；S+1.0F表示预应力、外荷载共同作用结果与收缩作用结果的线性叠加。

由图6可知，不考虑收缩作用(1.0F工况)钢顶板测点应力范围为-10.6～-24.6 MPa，钢底板应力范围为-14.5～-30.0 MPa，底板压应力略高于顶板；两端断面(G—F、B—A)应力变化显著，中间断面(F—B)应力变化相对平缓，G断面应力小于F断面。这是由于后承压板将钢箱梁受到的大部分力传递给混凝土梁，短距离内应力未完全扩散，造成后承压板附近的混凝土应力集中，钢箱梁应力偏低。B—A断面应力变化显著，主要是由于端部钢壳体和混凝土间的滑移量最大，剪力连接件传力作用显著。

对比1.0F工况和S1.0F、S+1.0F工况可知，考虑收缩作用后各断面平均应力显著增大，其中C断面钢顶板纵向正应力由23 MPa变化至50 MPa，增加了117.4%，钢底板纵向正应力由29 MPa变化至54 MPa，增加了86.2%，由此可知收缩作用对钢结构应力影响更为突出。对比S1.0F与S+1.0F的应力结果可知最大应力差出现在F断面，差值为5 MPa；其他各断面应力差别甚微，这表明由收缩作用引起的边界非线性并不明显。

由图7可知，不考虑收缩作用(1.0F工况)时，除两端断面外混凝土顶、底板的正应力变化均较为平缓。G—F断面的应力变化是由后承压板传力导致混凝土应力集中造成的，B—A断面的应力变化是由端部剪力连接件传力作用造成的。

混凝土顶、底板正应力在1.0F、S1.0F、S+1.0F工况作用下的变化趋势相似，均在G—E断面应力突变，应力均表现为先增加后急剧降低；收缩作用对混凝土应力分布影响明显，尤其是B、C断面，考虑收缩后，B、C断面顶板应力由2.5 MPa变化为1.0 MPa，减小幅度为60%。

比较1.0F、S1.0F及S+1.0F工况下1～44号栓钉、1～27号贯穿钢筋(编号见图5)的受力状况，见图8。

由图8可知，收缩作用对钢混结合段两端剪力连接件的受力影响显著。在靠近后承压板处栓钉承受的剪力由-1.2 kN变成4 kN；贯穿钢筋承受的剪力由10 kN变成17.5 kN，变化幅度为75.0%。比较S+1.0F和S1.0F的结果可知，收缩作用同样会造成后承压板的脱空，这种边界非线性会改变剪力的大小、方向。

5.2 徐变作用对钢混结合段受力的影响

由文献[9]分析知，徐变前期变形很快，尤其是前15 d近似呈线性变化，在计算龄期为23 d时，徐变变形占10年徐变总变形的56.7%，徐变3年变形已基本达到稳定。本文提取钢混结合段典型断面的钢、混凝土顶板、底板及腹板各测点的纵桥向瞬时正应力和考虑3年徐变后的正应力进行对比分析，其中钢、混凝土顶板对比结果见图9。经分析可得腹板、底板的应力分布规律与顶板基本相同，此处不再阐述。

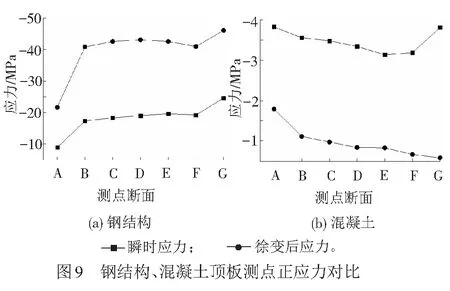
由图9(a)可知，钢结构顶板沿纵桥向各断面间的瞬时应力与徐变后的应力变化趋势类似。A—B断面应力显著升高，B—F断面应力近似维持定值，F—G断面应力再次升高。该应力变化规律表明钢混结合段两端剪力连接件传力作用明显。对比各测点断面的应力数值可知钢结构顶板徐变后应力最大值约是瞬时应力的2.35倍。

由图9(b)可知，混凝土顶板各断面间应力的变化规律与钢结构基本相同，但应力数值较低，瞬时应力为3.25～3.80 MPa，徐变后应力为0.6～1.8 MPa。除个别点外，混凝土顶板徐变后应力最大值约是瞬时应力的0.45倍。

研究表明徐变作用同样会影响剪力连接件的受力，其对顶板、底板和腹板产生的影响规律基本一致，在此仅列举徐变前后顶板栓钉纵桥向剪力数值的变化，见图10。

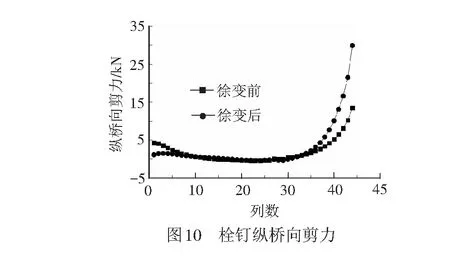
由图10可知，栓钉承受的剪力较小，集中在2 kN以内。徐变前、后栓钉纵桥向的剪力变化趋势近似相同，但考虑徐变后栓钉的剪力值均增大，其中后承压板处栓钉的剪力值由徐变前的12 kN变化到徐变后的30 kN，增大了150%，但各栓钉的受力仍远小于其抗剪极限承载力，表明考虑徐变作用后该结构仍具有较大的承载力安全储备。

6 收缩徐变对钢混结合段传力的影响

上述研究结果表明收缩、徐变作用会造成钢壳体与核心混凝土产生脱空现象和应力重分布，进而导致钢混结合段的传力规律及传力机制显著变化。提取各测点断面的应力进行积分可获得各截面内力，运用式( 1 )—式( 5 )计算钢混结合段考虑收缩作用、不考虑收缩作用和考虑徐变作用、不考虑徐变作用下的轴力传递指标，并绘制各传力曲线，见图11。

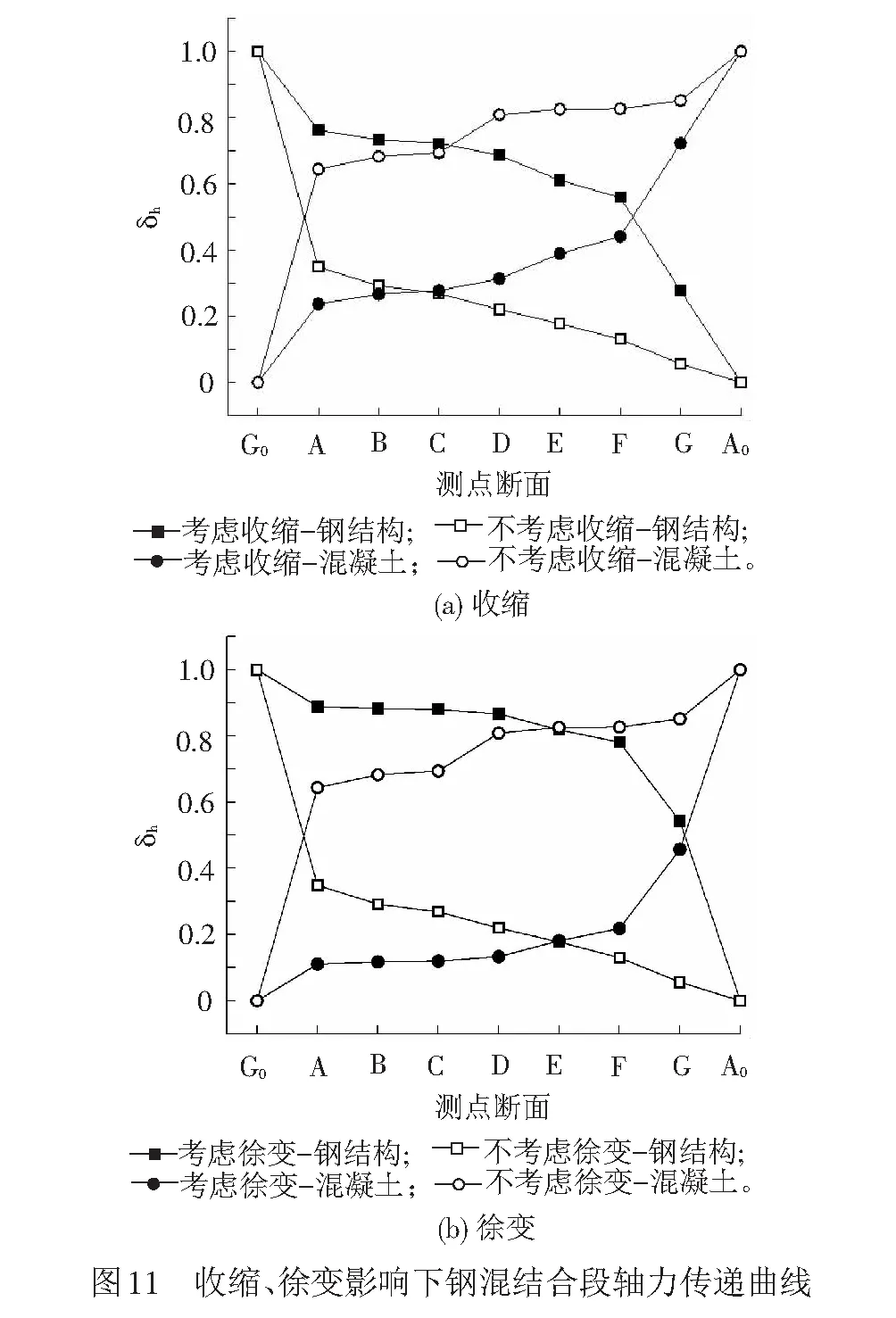
图11中A0、G0分别为混凝土断面、刚度过渡段断面。由图11(a)可知，考虑收缩作用后，后承压板传力率δh由58.50%减小至20.80%，传力平均斜率α由11.27%增大至19.20%，传力最大斜率αmax由49.33%增大至92.44%，传力均匀度δ由0.18增大为0.31。这说明收缩作用显著降低了承压板的传力作用，剪力连接件的传力作用增强。

由图11(b)可知，考虑徐变作用后，后承压板传力率δh由58.5%锐减至9.73%，传力平均斜率α由11.27%增大至27.86%，传力最大斜率αmax由49.33%增大至180.89%，传力均匀度δ由0.18变为0.62。这说明考虑徐变后承压板的传力作用降低幅度更大；两端剪力连接件受力更为显著，传力作用增强，因此钢混结合段整体受力状况更为不利。

7 结论

(1) 基于弹性徐变理论选取合适的指数型徐变度，可推导出不同徐变泊松比下复杂应力空间的混凝土徐变本构关系。根据此关系利用Fortran语言对Ansys中的材料本构关系进行二次开发，可实现对钢混结合段核心混凝土的徐变计算。

(2) 收缩作用对钢混结合段受力状况影响显著。其中钢结构压应力增大一倍，混凝土应力减小一半；剪力连接件承受的剪力增大，尤其是后承压板附近，增大幅度为75%。

(3) 徐变作用将引起钢混结合段的内力重分布。其中钢壳体压应力显著增加，徐变3年后的应力约是瞬时应力的1.9～2.47倍；而核心混凝土徐变3年后的应力约是瞬时应力的0.13倍。

(4) 收缩、徐变作用均显著改变了钢混结合段的传力模式。传力不均匀度分别提高了0.13、0.44；钢混结合段端部连接件承受的剪力变化幅度最大，分别增加了75%、150%。