考虑相邻出发列车车流分配的车辆集编排队系统分析
李 静,帅 斌,许旻昊,朱伟波,何春燕
(西南交通大学 交通运输与物流学院, 四川 成都 610031)
编组站是铁路运输的节点,有调中转车在编组站的集结过程是不可避免且耗时较长的技术作业环节。车辆集结结束条件与集结模式有关。传统集结模式包括定点集结和定编集结两种。对于定点集结模式,列车完全按图行车,只要确定发车时刻,编组结束时刻即可确定,出发条件对列车最小编成辆数没有限制;对于定编集结模式,只要编成辆数达到满轴编成辆数,则认为该集结过程结束。放宽条件定点集结模式是定点集结模式的过渡形式。该模式下,在编发时刻,如果集结车辆数不能满足满轴要求,但只要满足最小编成辆数约束,列车也可以正点出发。放宽条件定点集结模式同时考虑“按图行车”与列车最小编成辆数两个约束,与传统定点集结模式相比,增加了编成辆数约束,减少机车和区段能力浪费;与传统定编集结模式相比,提高了列车正点发车率,运输时效性得到改善,减少了车辆积压。基于以上特点,放宽条件定点集结模式比传统定点集结模式在实际生产中更容易付诸实践[1],对提高铁路运输组织灵活性、时效性和便捷性具有重要意义。
集结车辆到达调车场等待编发,该过程具有排队系统的一般特征,可以通过建立排队模型对车辆集结过程进行分析。关于车辆集编排队系统的研究,以往研究主要集中在传统的定点和定编两种模式[2-6],对放宽条件定点集结模式研究较少[7-8]。Petersen[2-3]建立了定点与定编集结模式下车辆单个到达成批服务的集编排队系统。Turnquist等[4]在此基础上,根据集结模式特点的不同,分别建立了两种车辆批量服务排队模型,并对列车编成辆数大小不作限制,这与实际不符。史峰等[5]建立了定编集结模式下车辆成批到达成批瞬时服务的随机服务系统,集结车辆数一旦达到满轴编成辆数,系统立马开始服务,服务时间为0。林枫[6]分别针对定点和定编两种集编系统建立了车辆批到达批服务排队模型。李静等[7-8]建立了放宽条件定点集结模式下车辆集编系统的批到达批服务排队模型。
以上研究没有考虑在放宽条件定点集结模式下,对相邻出发列车进行车流分配的情形。即考虑到同一去向后编列车可能丢线,先编列车在满足出发条件基础上,将部分本应随先编列车出发的车辆编组到后编列车,使得后编列车刚好满足出发条件,以保证两列车均正点出发[1]。针对该问题,本文构建了考虑相邻出发列车车流分配的车辆集编排队模型。首先,利用嵌入式马尔可夫链方法求得系统在发车时刻的车辆集结队长稳态分布,然后通过补充变量法得到系统在任意时刻队长稳态分布与发车时刻稳态分布的关系式,并对车辆平均集结队长、平均集结延误时间等系统指标进行分析,重点分析车流分配对系统性能的影响。
1 系统模型
1.1 模型说明
针对一个方向的车辆集编排队系统,将其抽象描述为由该方向集结车辆和相应列车编发系统组成的单队列单服务台排队模型。其中,“顾客”为集结车辆,“服务台”为列车编发系统。假设时间轴被分成等长时间段,称为时隙。不失一般性,时隙用0,1,2,…,t,…表示,则时间用时隙数表示。t-为车辆到达前时刻;t+为车辆离去时刻;*为任意时刻。为明确t时刻系统状态,约定车辆到达只能发生在时隙末端(t-,t),同时约定车辆离开,即系统服务开始或结束,只能发生在时隙首端(t,t+),车辆到达时刻示意见图1。本文排队模型采用具有延迟入口的晚到系统[9]。
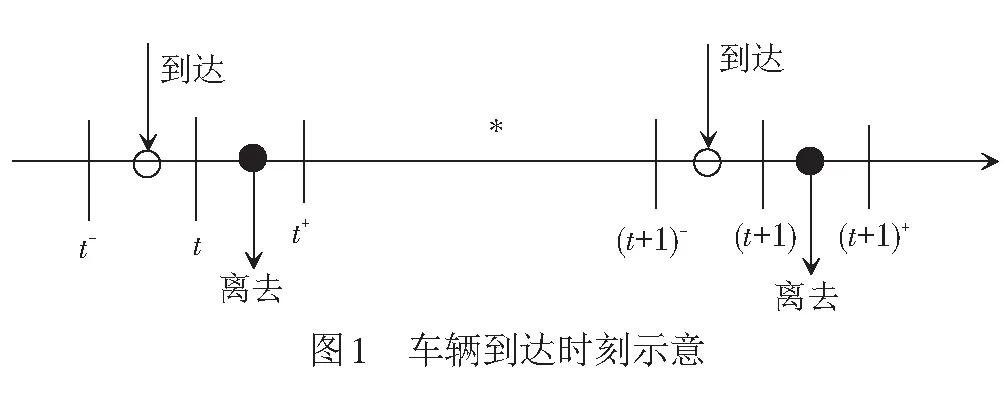
一般来讲,系统状态概率在到达前时刻,离去时刻与任意时刻是不相等的。
1.2 模型构建
(1) 到达过程
车辆以车组的形式批量到达,假设车组到达为Bernoulli过程,离散时间的Bernoulli到达过程相当于连续时间的Poisson过程[2,4,6,10-11],具有与Poisson到达过程一样的无后效性[12]。λ为车组到达强度,0<λ<1;X为1次到达车组包含车辆数,为正整数随机变量。其分布函数及母函数分别为
gm=P(X=m)m≥1
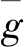
(2) 服务过程
列车图定发车时刻表已知,当不考虑调机运用及出发作业能力限制时,车辆在集编系统延误时间主要由等待出发时刻造成[4]。因此,假定最晚编组时刻与列车图定发车时刻之间的编组及出发作业时间为固定值[13],则列车图定发车时间间隔与最晚编组时间间隔具有相同的分布规律。为讨论方便,在文中不考虑最晚编组时刻与列车出发时刻之间的固定时间,将最晚编组时刻称为发车时刻,并将间隔时间用排队理论中的专门用语“服务时间”描述。
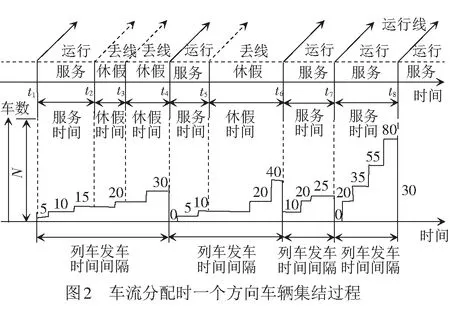
由此,定义从列车出发时刻起到下一个发车时刻之间的过程为排队系统的服务过程,服务过程持续时间为服务时间,也称为车辆集编排队系统处于运行期间。时刻t1与t2之间的过程为系统服务过程,见图2。S为服务时间,其概率分布st为
st=P(s=t)t=1,2,3,…
母函数S(z)为
假设系统服务时间与服务批量大小无关。系统运行结束只能发生在时隙首端(t,t+)期间内,此时,t+也称为系统运行结束时刻。
(3) 休假过程
在发车时刻,如果集结车辆数不能满足最小编成辆数约束,列车不能组织编发。如图2中,最小编成辆数l为25,满轴编成辆数c为50,t2时刻系统内集结车辆数为15,小于最小编成辆数,该情形下,列车丢线,车辆继续集结,等待下一条运行线。从列车丢线时刻起到下一个出发时刻为止之间的过程称为排队系统的休假过程,也称为车辆集编排队系统处于丢线期间。如时刻t2与t3之间的过程为系统休假过程。V为休假时间,其概率分布vt为
vt=P(v=t)t=1,2,3,…
母函数V(z)为
当车列提前或延迟集结结束,不考虑加线。同样系统丢线结束只能发生在时隙首端(t,t+)期间内,此时,t+称为系统丢线结束时刻。
在发车时刻,只要系统内集结车辆数不能满足最小编成辆数要求,列车可能多次丢线。如图2所示,在t3时刻,系统内集结车辆数为20,还是小于最小编成辆数,在上一次丢线结束以后,列车再次丢线。
从以上描述可知,系统运行结束及系统丢线结束时刻等同于车辆离去时刻,在文中统称为发车时刻。
(4) 排队规则
N为某集结方向最多等待车辆数,则系统内最多车辆数为N+c(c≤N),并假设当容量限制时,到达车组可以拆分,即部分车辆进入调车场,剩余车辆不能进入。车辆按照先到先服务的规则等待编发。
(5) 服务规则
在发车时刻,车辆集结队长为n时,先编列车在满足出发条件基础上,将部分本应随先编列车出发的车辆编组到后编列车,使得后编列车刚好满足出发条件。服务批量大小等于列车编成辆数,该参数为同时受列车最小编成辆数与满轴编成辆数限制的正整数随机变量。
在发车时刻,相邻出发列车不分配车流的情形包括:
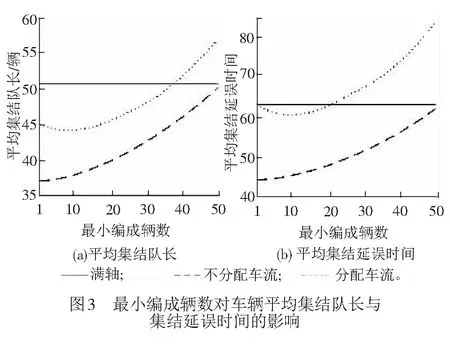
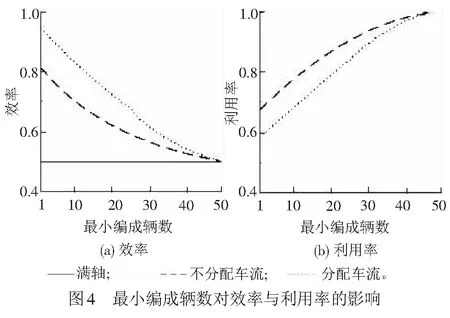
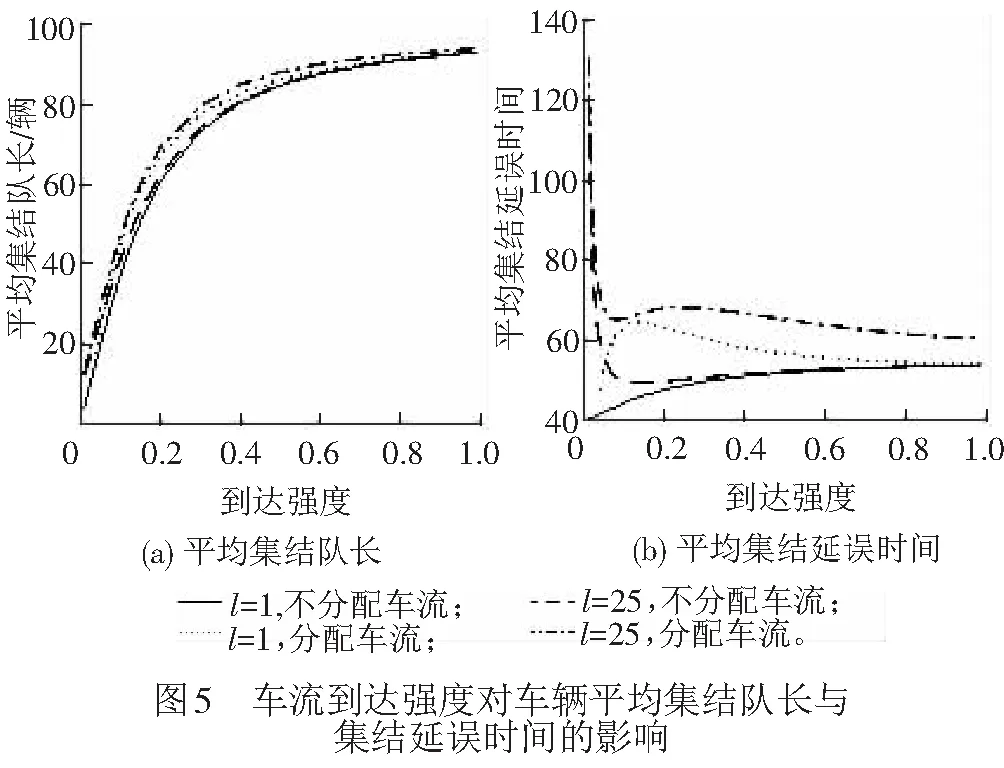
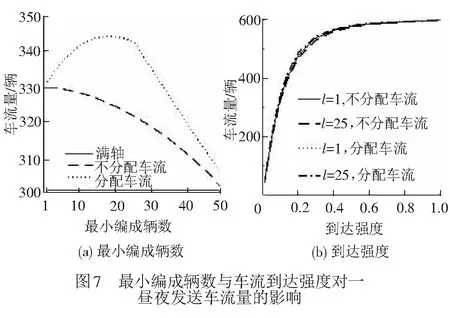
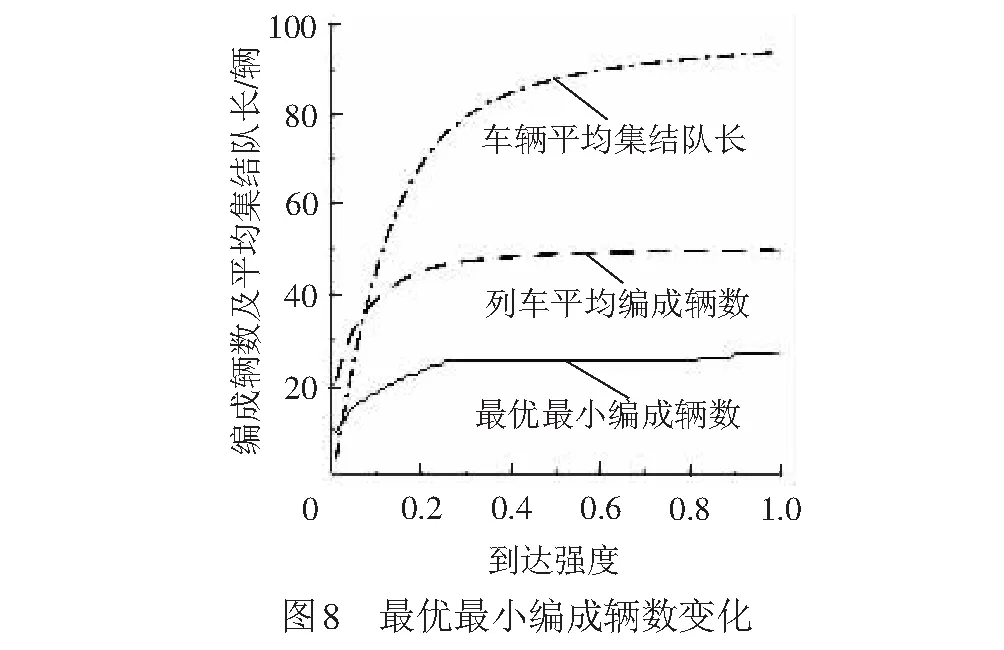
① 车辆集结队长n ② 车辆集结队长n=l时,组织所有车辆编发,系统进入运行过程,剩余车辆数为0,该情形下,先编列车不用为后编列车分配车流。 ③ 车辆集结队长n满足l+1≤n≤min(c+l-1,N)时,存在两种情形不需要进行车流分配:一是当先编列车编成辆数为最小编成辆数l时,能为后编列车分配的最大车辆数为(n-l),当前列车出发以后,系统运行期间内到达车辆数与剩余车辆数之和仍然小于最小编成辆数,该情形下不分配车流。因为即使最大限度的为了保证两列车均正点出发,还是不能满足后编列车的出发要求,宁可将集结车辆编入先编列车出发,从而减少车辆集结时间。二是当先编列车满轴出发以后,剩余车辆数与当前列车运行期间内到达车辆数之和能够满足后编列车最小编成辆数约束,该情形下,先编列车不用为后编列车分配车流。 ( 1 ) 以图2为例对上述分配车流规则进行说明。在发车时刻t2与t3处,集结车辆数均小于最小编成辆数,列车连续两次丢线,先编列车不用为后编列车分配车流。t4时刻,车辆集结队长为30,大于最小编成辆数,且估计到系统运行期间能够到达的车辆数为15,先编列车最多能为后编列车分配的车辆数为5,后编列车仍然不能满足出发条件,因此,先编列车不为后编列车分配车流,组织所有车辆编发,剩余车辆数为0。t5时刻,集结队长为15,小于最小编成辆数,列车丢线,先编列车不用为后编列车分配车流。t6时刻车辆集结队长为40,大于最小编成辆数,且估计到系统运行期间能够到达的车辆数为15,为了保证后编列车也能正点出发,t6时刻,列车不全部编发所有集结车辆,而是只编组前30辆车,为后编列车留下10辆,使得后编列车也能刚好满足出发条件。t7时刻,本应随t6时刻列车出发的10辆集结车辆,再加上t6与t7时刻之间到达的15辆车,列车刚好能够满足出发条件,立即组织所有车辆编发,先编列车同样不用为后编列车分配车流。t8时刻,系统内车辆集结队长为80,当前列车即使满轴编发,剩余车辆数为30,后编列车也能够满足出发条件,所以先编列车不用为后编列车分配车流。 假设以上随机过程均具有平稳性与各态历经性;在安排发车时,暂不考虑机车运用、区段通过能力和技术站作业能力的限制。 系统只有在发车时刻才具有马尔可夫性,因此,设定发车时刻车辆集结队长为系统状态变量,利用嵌入式马尔可夫链方法得到发车时刻系统状态的平稳分布。对于成批到达的系统,发车时刻与任意时刻的车辆集结队长不服从相同分布[14]。因此,为了得到任意时刻车辆集结队长分布,需要寻求其与发车时刻队长分布之间的关系。 式中:S为系统处于运行状态;V为系统处于丢线状态;矩阵SS,SV,VS,VV分别表示系统在运行和丢线两种状态之间转移。根据系统描述可知:SSε=VSε,SVε=VVε。由于对相邻出发列车进行车流分配,分配车流方案一步状态转移概率矩阵在不分配车流方案基础上发生变化。发生变化情形是在发车时刻车辆集结队长大于最小编成辆数时,即当系统状态转为运行状态时,由于SS1=VS1,这里只讨论SS1情形。SS0为不进行车流分配时一步状态转移概率矩阵,SS附加为对车流进行分配时一步状态转移矩阵发生的变化,两者之和即为分配车流情形下的一步状态转移概率矩阵,表示为SS1=SS0+SS附加。具体计算公式为 式中: j>0k≥1 1≤n≤N-1 k≥1 0≤a≤l-1 1≤n≤N-1-a 当j+c≥2l时,δj+c=1,否则δj+c=0。 定义联合概率 σn(r,t-)=P(Nt-=n,Rt-=r,εt-=1) 0≤n≤Nr≥0 ωn(r,t-)=P(Nt-=n,Ht-=r,εt-=0) 0≤n≤Nr≥0 稳态条件下有 σn(r)=limt-→∞σn(r,t-) ωn(r)=limt-→∞ωn(r,t-) 对应母函数分别为 |z|≤1 0≤n≤N 当l ( 2 ) ( 3 ) (1-λ)[σc+n(0)+ωc+n(0)]l+1≤n≤N-c-1 ( 4 ) ( 5 ) ( 6 ) 当l≥N-c时 ( 7 ) ( 8 ) ( 9 ) (10) (11) ω0=(1-λ)ω0-(1-λ)ω0(0)+(1-λ)[σ0(0)+ω0(0)] (12) (13) (14) (15) (16) (17) 式中:E(S)、E(V)分别为平均服务时间、均值。 由式( 2 )~式(17)可求得{σn,ωn}。 (1) 车辆平均集结队长 系统任意时刻车辆集结队长为n的概率pn为 pn=σn+ωn0≤n≤N 则车辆平均集结队长Lq为 (18) (2) 车辆平均集结延误时间 Wq为车辆平均集结延误时间,表示任意待集结车辆在编发系统内集结等待的平均时间。由于车辆平均集结延误时间与平均集结队长之间满足Little关系,因此,车辆平均集结延误时间为 (19) (3) 效率 用任意时刻系统处于运行过程概率来反映编发系统工作效率,则编发系统处于忙期概率ρb为 (20) (4) 利用率 列车牵引能力利用率p利用率为列车平均编成辆数与满轴编成辆数的比值,则 p利用率=Ls/c (21) (5) 一昼夜发送车流量 E为一个方向车辆集编排队系统一昼夜服务完成后离开的车辆数为一昼夜发送车流量 E=n图×ρb×Ls (22) 式中:n图为该方向一昼夜图定平均发送列车数,n图=24/E(S)。 车流到达强度λ=0.1时,分配车流方案的车辆平均集结队长与集结延误时间均随着最小编成辆数增加而先减小后增大,不分配车流方案的车辆平均集结队长与集结延误时间均随着最小编成辆数增加而单调递增,见图3。分配车流方案车辆平均集结队长和集结时间均大于不分配车流方案,在最小编成辆数较大时,甚至大于采用满轴编成辆数时集结队长和时间,因此,从节省车辆集结时间角度,对相邻出发列车进行车流分配是不利的。 最小编成辆数对效率与利用率的影响见图4。由图4可见,编发系统工作效率随着最小编成辆数增加逐渐下降,利用率逐渐上升,分配车流方案效率高于不分配车流方案,但利用率低于不分配车流方案,表明对相邻出发列车进行车流分配增加了列车正点发车概率,但出发列车平均编成辆数会有所下降。 当最小编成辆数l分别为1、25时,车辆平均集结队长与集结延误时间随车流到达强度变化的趋势,见图5。由图5(a)可见,随着车流到达强度增加,车辆平均集结队长增加,但分配车流方案集结队长大于不分配车流方案;由图5(b)可见,当l=1时,即在定点集结模式下,分配车流方案的车辆平均集结延误时间随着车流到达强度增加而先增加后减小并逐渐趋近于平稳。可以解释为,当车流到达强度较小时,本应随先编列车出发的车辆为了等待后编列车而增加了延误时间;当车流到达强度继续增大,该类延误时间减小,车辆平均集结延误时间呈现下降趋势;随着到达强度继续增大,车辆需要在站集结等待列车运行时刻,且由于容量限制,超过容量限制的车辆不能进入系统,车辆集结延误时间逐渐趋近于平稳。当l=25时,分配车辆方案车辆集结延误时间随车流到达强度增加而先减小后增大直至趋近平稳,分配车辆方案与不分配车流方案车辆集结延误时间随车流到达强度具相似的变化趋势。但分配车流方案车辆集结延误时间始终大于不分配车流方案。 车流到达强度对效率与利用率的影响见图6。由图6(a)可见,车流到达强度越大,列车出发运行的概率越高,编发系统的工作效率越高,分配车流方案效率高于不分配车流方案;图6(b)表明车流到达强度越大,列车平均编成辆数越大,列车牵引能力利用率越高,分配车流方案能力利用率小于不分配车流方案,随着到达强度增加,分配车流方案和不分配车流方案的利用率均趋近于1。 当λ=0.1时,一昼夜发送车流量受到最小编成辆数变化的影响见图7(a)。最小编成辆数与不分配车流方案一昼夜发送车流量呈负相关,即最小编成辆数等于1时,该方向一昼夜发送车流量最多。分配车流方案一昼夜发送车流量随着最小编成辆数增加而先增加后减小,最小编成辆数较小时,车流分配增加了列车发车概率,运行线能力较不分配车流方案得到了更好利用;但随着最小编成辆数增大,列车丢线概率增加,丢线导致发送车流量下降。分配车流方案一昼夜发送车流量大于不分配车流方案。同时,随着到达强度增大,分配车流方案与不分配车流方案的发送车流量均呈现增长趋势,两者变化规律基本一致,见图7(b)。 定义最优最小编成辆数为使得该方向一昼夜发送车流量最大的最小编成辆数。当不分配车流时,最优最小编成辆数始终等于1,见图7(a)。当分配车流时,最优最小编成辆数及对应列车平均编成辆数和平均集结队长变化趋势见图8。随着到达强度增加,最优最小编成辆数增加,到达强度较小时,最优最小编成辆数增长较快,到达强度较大时,增长趋于平稳。该算例中到达强度在[0.25,0.81]区间变化时,最优最小编成辆数恒为25。车辆平均集结队长和列车平均编成辆数随着车流到达强度增加而增加,当到达强度足够大时,列车平均编成辆数基本等于满轴编成辆数,车辆平均集结队长逐渐增大并逐渐趋近系统容量限制。 本文将车辆在站集结过程描述成具有容量限制的采用多重休假策略的批到达批服务离散时间排队模型。考虑相邻出发列车车流分配,引入了车流分配机制,得到了稳态条件下发车时刻及任意时刻车辆集结队长分布,并得到了系统指标的数学表达式。最后,通过算例,针对分配车流方案与不分配车流方案的系统指标及最优最小编成辆数变化规律进行了对比分析。 算例结果表明:(1)分配车流方案较不分配车方案,车辆的平均集结队长与平均集结延误时间均较长,从减少车辆集结延误时间角度,对相邻出发列车进行车流分配是不利的。(2)对相邻出发列车进行车流分配使得列车平均编成辆数减小,但由于提高了发车时刻列车正点发车概率,综合起来表现为分配车流方案一昼夜发送车流量较大。因此,从增加一昼夜发送车流量角度,对相邻出发列车进行车流分配是有利的。(3)分配车流方案的最优最小编成辆数随着到达强度增加而逐渐增大,不分配车流方案的最优最小编成辆数则始终等于1。
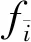
2 系统稳态分布
2.1 发车时刻车辆集结队长分布


2.2 任意时刻车辆集结队长分布
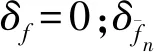
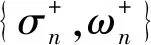

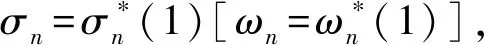
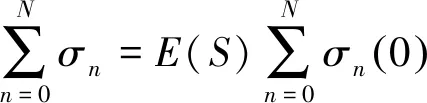
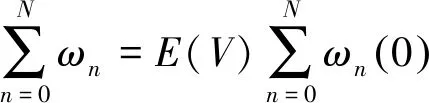
3 系统性能指标

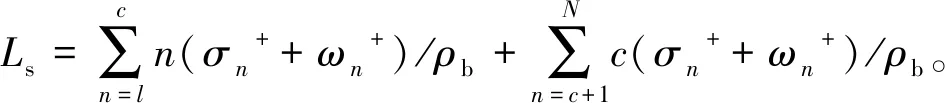
4 算例分析
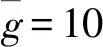

5 结束语

