车轮高阶不圆对轮对蛇行运动和等效锥度的影响

干 锋, 戴焕云, 宋春元,2, 沈文林

(1. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 2. 中车长春轨道客车股份有限公司， 吉林 长春 130062)

铁路车辆车轮由于外形的机械加工和实际线路运行过程中的滚动磨损等因素，容易出现在滚动圆周方向不圆现象 ，其形成和演化过程的机理非常复杂，且在每个铁路系统的轮轨中几乎都存在[1]。同时在车辆运行过程中，车轮不圆对轨道扣件、轨枕、轮对、轴箱端盖和构架零部件等造成较大损伤，成为轮轨接触关系研究的难题之一[2-3]。国内近几年高速动车组车轮不圆现象非常严重，已成为铁路运输系统中急需解决的[2]和影响高速列车的关键力学问题[3]。测试某型高速动车组车轮镟修后运行里程在15万～25万km范围内的2 451个车轮的圆周不圆廓形，发现多边形显著(表面粗糙度大于18 db)的比例高达16.6%，10万～15万km的比例也达到9.5%。车轮高阶不圆阶数高达17～23阶，同时10 kHz采样发现产生高达200g以上的轴箱振动加速度，导致轴箱盖螺栓断裂，严重影响列车正常运营和车辆关键部件的使用寿命。

针对车轮不圆，国内外学者在试验检测和数值模拟方面展开了一些研究。文献[4-5]测试了大量的车轮不圆外形，给出车轮不圆表面粗糙度和多边形阶数的计算方法，实测和仿真了钢轨高频振动频响以及带缺陷车轮通过轨道时的轮轨力，并通过数学模型的校准和验证。Barke等[6]认为车轮擦伤和剥离下轮轨动态作用力会导致车轮产生圆周方向的不圆。Meywerk[7]考虑弹性轮对和钢轨并建立柔性动力学模型，将车轮不圆作为轮轨系统的不平顺激扰得到车轮和钢轨的振动，同时结合磨耗理论仿真分析了车轮多边形的发展历程，结果表明车轮多边形的形成主要是由于轮对的一阶和二阶弯曲模态，且列车的运行速度和轨道结构参数对车轮不圆顺的形成有一定的影响。

张雪姗等[8]研究了车轮椭圆化问题及其对车辆横向稳定性的影响。陈光雄等[9]分析了车轮多边形的磨耗机理， 并指出了相应的控制策略。宋春元等[10]从车轮多边形与运行速度、运行线路条件、车辆结构等角度研究车轮多边形对车辆振动的影响，研制了踏面研磨装置，在运营过程中施加以消除多边形，并改善踏面凹形磨耗。沈文林等[11]对我国CRH3型动车组车轮不圆外形进行了大量现场的测试，并从车轮材质、热处理、组装工艺、 硬度等方面开展调查，发现提高车轮硬度可以抑制车轮多边形产生。韩光旭等[12]通过高速列车长期跟踪试验，发现现有的不落轮式车轮镟修加工手段， 不能完全消除车轮非圆化磨耗的再次形成和发展，同时车轮不圆会引起异常的振动噪声。

现阶段国内高速列车车轮高阶不圆现象比较严重，虽然进行了大量不圆外形测试和统计规律分析，但其形成机理没有很好的理论支撑[2]。我国高速列车车轮不圆的阶次较高，主要集中在17～23阶，在轮轨间可产生高达 580 Hz 左右的高频冲击[13-14]，严重威胁高速列车的运营安全，导致一系列车辆和轨道结构疲劳失效问题，见图1。为了分析高速列车在车轮不圆下的运动稳定和行车安全，需要从轮轨接触关系本身出发研究其对轮对蛇行运动稳定性的影响。

1 轮对蛇行运动及等效锥度分析

铁道车辆在轨道上运行，依靠一定形状的车轮踏面和钢轨轨面相互配合来完成直线行走和曲线通过等运动。由于车轮踏面带有一定锥度，在轨道上运行会产生一种特有的自激振动，表现为轮对横向移动时伴随绕其中心的垂向转动，这种运动称为轮对蛇行运动。绘制轮对中心线的横向运动轨迹可以发现轮对蛇行运动具有特定的波长，见图2，其中v为车速，λ为轮对蛇行波长。

1.1 UIC 519—2004[15]标准蛇行波长和等效锥度计算

计算等效锥度的方法有多种，最简单的方法为锥形踏面的等效方法(简化法)，UIC 519—2004[15]标准中等效锥度计算采用轮对随机运动的假设，并定义轮对蛇行运动幅值为3 mm时所对应的等效锥度为名义等效锥度；而欧洲标准则采用周期正弦波的假设(谐波法)，并将其引入到等效锥度的计算方法中[15-16]。

对于锥形踏面的车轮，在滚动圆附近可看做一段锥度为常值γ的直线段。当不考虑轮对横移运动产生的侧滚时，轮对在一定的横移量y下左右车轮对应的接触半径分别为rL、rR，接触半径差为Δr，此时的锥度γ为

( 1 )

对于实际的车轮踏面外形，γ不是一个常数，而是随着y的变化而变化。根据左右车轮滚动接触半径rL、rR计算出的踏面锥度为等效锥度。

对于自由轮对在轨道上的运动，可由微分方程来描述

( 2 )

式中：e为接触点跨距；r0为名义滚动圆半径。

若假设车轮踏面外形为φ角的锥形为

Δr=2ytanφ

( 3 )

则微分方程变为常系数二阶微分方程

( 4 )

其解为波长λ的正弦波

( 5 )

若车轮踏面外形不是锥形，可采用线性化法，在微分方程中以tanφe取代tanφ进行线性化。tanφe称作等效锥度。

通过对给定初始幅值y=y0的积分，可导出轮对以峰-峰或谷-谷幅值2y和波长λ的周期运动。应用Klingel公式计算等效锥度

( 6 )

1.2 自由轮对蛇行运动推导

结合图2中的蛇行运动过程，在xy平面坐标系中，从以下两方面进行分析。

1.2.1 轮对有横移无摇头时

当轮对有横移无摇头，即y0，θ=0时，左轮接触半径为Rl，右轮为Rr，左轮接触点距轮对中心距离为Ll，右轮为Lr,见图3(a)。此时车轮以ω的角速度向前滚动时，左轮接触点的滚动速度为vl，右轮为vr，则

( 7 )

当vl>vr时，轮对的瞬时摇头中心o′在轨面右侧，反之o′在轨面左侧。

此时摇头角速度φ可由下式得出

( 8 )

由此摇头中心o′距右侧接触点的距离Rφ和摇头角速度φ分别为

( 9 )

轮对前进速度

(10)

此时车轮在轮对坐标系下的瞬时前进速度v0与在轨道坐标系下的前进速度v一致，即v=v0。

1.2.2 轮对有横移、摇头时

当轮对有横移、摇头时，轮对前进速度与车轮沿轨道运行速度具有一定的摇头角θ，此时车轮沿轨道运行速度v=v0cosθ，轮对横移速度vy=v0sinθ,见图3(b)。

由此得到以下微分方程

(11)

2 轮对蛇行运动及等效锥度对比分析

以S1002CN踏面和CHN60轨面为例,见图4。采用矢量法[17]实时计算轮轨接触点并求解微分方程式(11)，计算轮对初始横移3 mm下的蛇行运动，见图5。

从图5可以看出，当给定初始轮对横移量为3 mm时，轮对将做3 mm的蛇行运动，同时轮对的横移和摇头相位角相差90°。

由此得到横移或摇头波长，可根据Kklingel公式得到此时轮对横移量下的等效锥度值。

2.1 车轮踏面蛇行波长和等效锥度分析

计算0～12 mm轮对横移量下蛇行运动波长和等效锥度，并与UIC 519—2004[15]标准结果进行对比，见图6。

由图6可以看出，由自由轮对蛇行运动公式得到的等效锥度和蛇行运动波长变化与文献[15]得到的结果一致。

为了更好验证这个结论，采用磨耗后的S1002CN踏面进行分析。磨耗后车轮踏面外形见图7，计算等效锥度和蛇行运动波长见图8。

由图8可以看出，对于磨耗后的车轮踏面，自由轮对蛇行运动公式得到的等效锥度和蛇行运动波长与UIC519计算结果也是基本一致的。

2.2 运行速度对自由轮对蛇行运动波长的影响

分别计算列车运行速度为100、200、300 km/h时，标准踏面和磨耗后踏面在轮对横移3 mm时的蛇行运动波长，见图9。

由图9可以看出，在不同运行速度下轮对的蛇行运动一致，这同时也说明轮对的蛇行运动波长与运行速度无关。

2.3 不同速度下自由轮对蛇行运动频率分析

根据标准S1002CN踏面和磨耗踏面的蛇行运动波长，计算列车运行速度在300、200、100 km/h下的蛇行运动频率，见图10。

由图10可以看出，对于同一个踏面外形，蛇行运动频率随运行速度成比例增加；对于磨耗后踏面外形，其蛇行运动频率大于标准踏面的蛇行运动频率。

分别分析S1002CN、LMA、XP55和LM 4种标准踏面蛇行运动波长、等效锥度以及在不同运行速度下的蛇行运动频率，见图11、图12；不同类型车轮踏面在不同运行速度下自由轮对的失稳频率见表1。

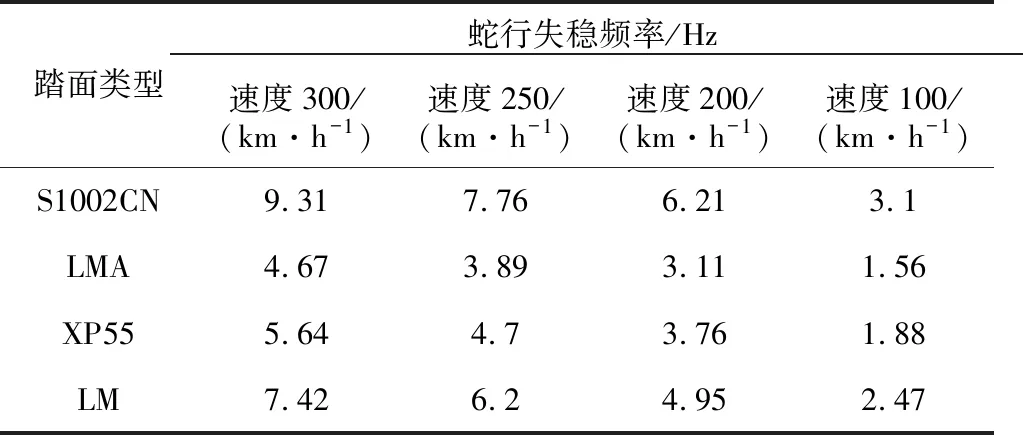
表1 不同踏面类型和运行速度下自由轮对失稳频率

3 车轮多边形对蛇行运动的影响

对于车轮多边形，通常在车轮圆周方向出现一定波长的轮径波动，测量车轮一周，轮径成锯齿形变化，最大径跳量达到0.103 mm,见图13。

为了描述车轮不圆，在轮对蛇行运动过程中，左右车轮接触半径可简化描述为

(12)

式中：Rl0、Rr0分别为左右轮初始接触半径；Al、Ar分别为左右车轮径跳量；Nl、Nr分别为左右车轮不圆度阶数；θ为轮对转角；σ为左右车轮不圆相位差。

为了验证车轮不圆对蛇行运动的影响，令轮对初始前进速度为300 km/h，Al=Ar=0.05 mm，Nl=Nr=20，σ=0°，计算得到单个蛇行周期内车轮运行姿态的变化，并与无车轮不圆时的结果进行对比，见图14、图15。

由图14和图15可以看出：

(1) 对于标准S1002CN踏面，有无车轮不圆时蛇行运动波长和等效锥度无明显变化。

(2) 有车轮不圆时轮对纵向速度、横向加速度、摇头角速度和左右轮接触半径变化明显，且波动频率明显增加，为578 Hz。

(3) 有无车轮不圆时车轮横向位移、速度和摇头角度变化不大。

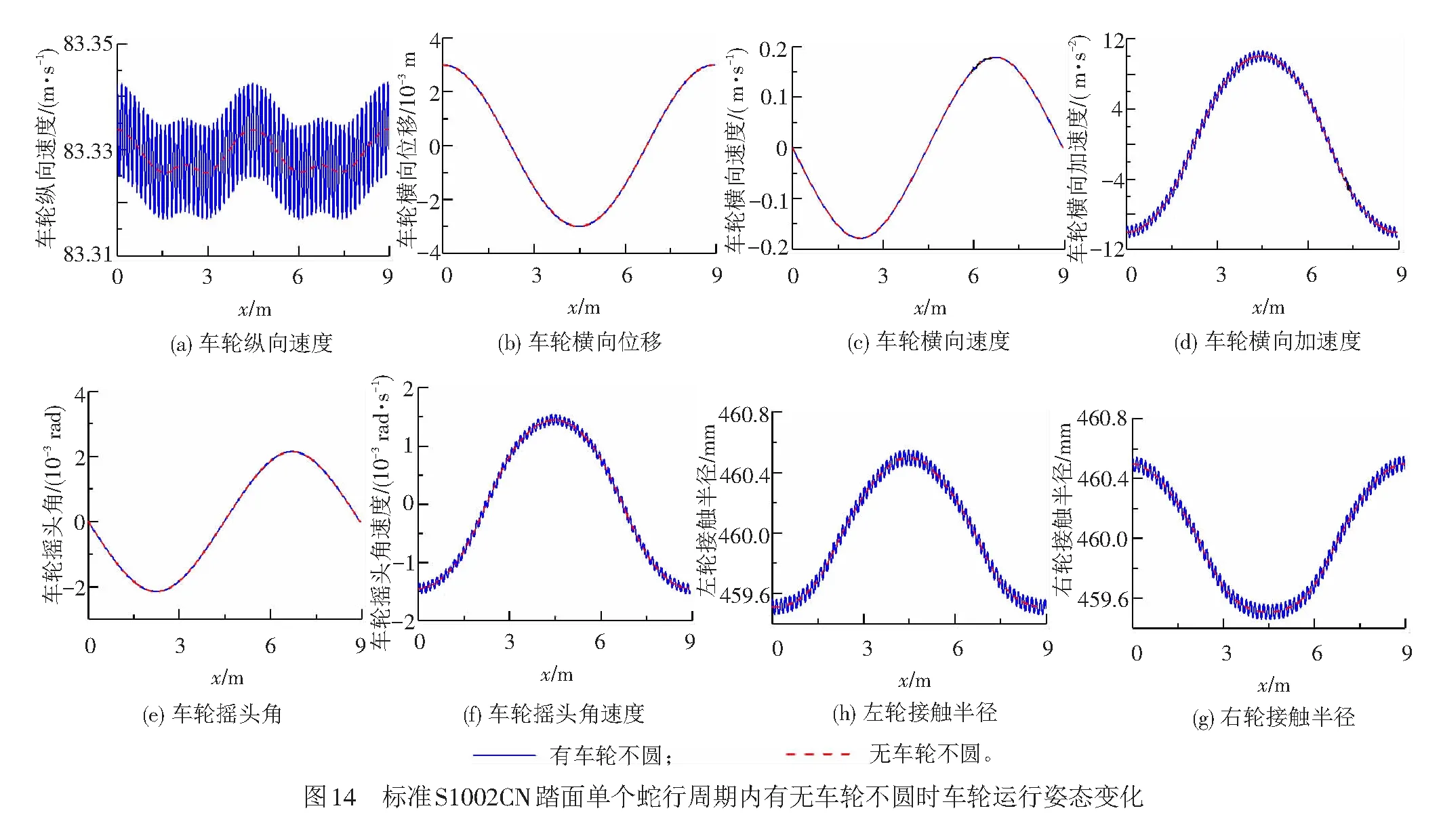
这是由于有0.1 mm车轮径跳量的存在，会使S1002CN踏面的轮径差向上或向下偏移0.1 mm，轮对横移范围见图16。以轮对横移3 mm为例，无车轮不圆时的轮径差为0.99 mm；当有车轮不圆时，为了保持相同的轮径差，车轮的横移范围在2.7～3.4 mm之间。因此车轮径跳0.1 mm时等效的相对轮对横移范围为-0.3～0.4 mm。此时轮径差未改变，通过积分运算得到的轮对蛇行波长不会有大的变动，但等效的相对轮对横移量有变化，会引起轮对纵向、横向和摇头运动的高频振动。

对于磨耗后的车轮踏面，同样分析有无车轮不圆时蛇行运动波长和等效锥度的变化，见图17。

由图17可以看出，对于磨耗后S1002CN踏面，有无车轮不圆时蛇行运动步长和等效锥度基本不变。

4 结论

(1) 求解推导的与轮对横移、摇头相关的3个一阶蛇行运动微分方程与轮对横移相关的二阶微分方程得到一致的结果，结合Klingel公式也得到一致的等效锥度曲线。

(2) 给出4种轮轨匹配在不同速度下自由轮对的等效锥度、蛇行波长和蛇行频率，表明等效锥度和蛇行波长与运行速度无关，蛇行频率与速度线性相关，速度越高蛇行频率越高。

(3) 根据实测车轮圆周方向不圆度曲线，得到车轮高阶不圆度，代入推导的蛇行运动公式中得到车轮高阶不圆下蛇行运动特征。表明车轮高阶不圆对轮对纵向速度和摇头角速度影响明显，对轮对横移量和摇头角度影响不明显，因此对自由轮对蛇行频率和等效锥度影响也不明显。

(4) 当车轮径跳0.1 mm时，在轮对横移3 mm下，等效相对轮对横移范围为-0.3～0.4 mm。此时轮径差未改变，通过积分运算得到的轮对蛇行波长不会有大的变动，但等效相对轮对横移量有变化，会引起轮对纵向、横向和摇头运动的高频振动。对于20阶车轮不圆，车轮初始速度300 km/h运行时，振动频率高达578 Hz。

(5) 在本文给出的自由轮对蛇行运动方程基础上，下一步可考虑轮对蛇行运动对构架和车体蛇行运动的影响，并研究车轮的高频激励对车辆振动的影响。