桥梁徐变效应的有限元算法研究及程序验证

王雨权,廖立坚,李林安,霍学晋,李 黎

(1.中国铁路设计集团有限公司,天津 300308； 2.天津大学力学系,天津 300350； 3.中铁大桥勘测设计院集团有限公司,武汉 430050； 4.中铁第六勘察设计院集团有限公司,天津 300308)

在应力状态下，徐变是混凝土的固有特性。混凝土长期徐变会引起桥梁结构发生主要受力方向的位移，因此，徐变计算是桥梁，尤其是大跨度桥梁结构的控制性因素[1-5]。设计及研究人员对于徐变引起的各种不利影响进行了深入研究，如徐变引起CRTSⅡ型纵连板式轨道和桥面之间的脱空现象[6]，徐变对剪力滞效应影响[7]等。因此，鉴于徐变的重要性，很多学者也对如何更好地模拟徐变效应进行了深入研究[8-12]。

人们可通过徐变系数来描述徐变现象，查阅相关文献可知，徐变系数的影响因素很多，其表达式的模型也很多[13-15]，国内公路规范[16]和铁路规范[17]代表了两种表达形式。

如何利用规范上的徐变系数进行精确合理地计算混凝土桥梁的徐变效应，是一个较难确定的复杂问题。由于商业软件Midas Civil操作简便性，在一般设计中，设计人员很少去深究徐变到底是如何计算的。而对于Midas Civil来说，徐变计算模块是其核心功能模块，运算机理一直处于保密状态。因此，设计人员对于该模块的计算过程其实是处于一个黑盒子状态[18-20]。这对于准确把握设计精髓，进一步提高桥梁设计水平有阻碍作用。因此，进行徐变算法的相关研究工作十分必要。

从徐变系数出发，以Midas Civil帮助文件中涉及到的算法为参照，深入研究相关计算方法，并进行相应的公式推导。在确定算法路径后，详细给出了递推格式的计算公式和步骤，并进行了相关案例测试。

1 徐变系数

影响混凝土徐变的因素很多，但主要因素有混凝土强度、受荷时的混凝土龄期、周边环境相对湿度、温度、混凝土体积、作用于混凝土结构的持续应力大小等。为计算徐变引起的变形，引入徐变系数φ(t，τ)的概念。

徐变系数φ(t，τ)可表示为从时刻τ开始作用一个应力σ(τ)后，混凝土在时刻t时的单轴应变与加载龄期τ时的应变之比。即

(1)

式中，εcr(t，τ)为龄期为τ的混凝土在时刻t时应变；εe(τ)为加载时刻的弹性应变。

目前，国内外对徐变效应考虑的因素不尽相同，采用了不同的数学表达方式，但归纳起来有以下两大类。

一是将徐变系数表达为一系列系数的乘积，每一个系数表示一个影响因子。如BS5400英国规范(1984年版)、美国ACI209标准(1982年版)、CEB-FIP标准规范(1990年版)、JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》。

二是将徐变系数表达为若干个性质互异的分项系数之和。如CEB-FIP标准规范(1978年版)、JTJ 023—85《公路钢筋混凝土及预应力混凝土桥涵设计规范》(1985年版)、TB 10092—2017《铁路桥涵混凝土结构设计规范》等。

目前，国内有关桥梁徐变系数的相关规定，主要采用公路和铁路两个行业规范。TB 10092—2017《铁路桥涵混凝土结构设计规范》(以下简称“《2017年铁路桥规》”)附录A给出了徐变系数的相关规定。该规范沿用了历年桥梁规范规定，徐变系数的计算表达式中，存在很多图表。JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称“《2018年公路规范》”)附录C也给出了徐变系数的相关规定，该规范在上一版规范的基础上，增加了添加粉煤灰的混凝土徐变修正系数。对于一般混凝土材料，仍然维持上一版规定。下面对这两本规范的内容进行简要介绍。

1.1 公路规范相关规定

《2018年公路规范》的徐变系数采用乘积形式，具体表达式如下。

(2)

式中，t0为加载时的混凝土龄期，d；t为计算考虑时刻的混凝土龄期，d；φ(t，t0)表示加载龄期为t0，计算考虑龄期为t时的混凝土徐变系数；φ0为名义徐变系数；βc(t-t0)为加载后徐变随时间发展的系数；βH为与年平均相对湿度相关的系数；fcm为强度等级C20～C50混凝土在28 d龄期时的平均立方体抗压强度，MPa；fcm0取值10 MPa；RH为环境年平均相对湿度，%；RH0取值100%；h为构件理论厚度，mm，h=2A/μ，A为构件截面面积，μ为构件与大气接触的周边长度；h0取100 mm；t1取1 d。

1.2 铁路规范相关规定

《2017年铁路规范》的徐变系数采用分项系数相加的形式，具体表达式如下。

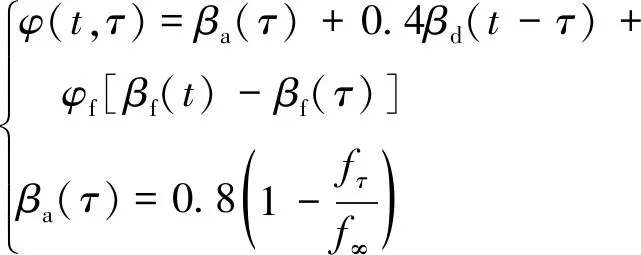
(3)

式中，φ(t，τ)为徐变系数；βd(t-τ)为随时间而增长的滞后弹性应变，取值查规范附录图A.0.2-1；fτ/f∞表示加载时混凝土的强度与最终强度R∞之比，查规范附录图A.0.2-2；φf为流塑系数，φf=φf1×φf2；φf1为依周围环境而定的系数；φf2为依理论厚度h而定的系数，查规范附录图A.0.2-3。

两本规范的表达式相差很大，公路规范的表达式明确，而铁路规范的相关系数取值依赖于图表的查询，这容易产生徐变系数取值误差。

2 徐变算法对比研究

混凝土徐变的计算方法大致有Dischinger微分求解法、Tröst-Bazant代数求解法和有限元逐步增量法。对于结构形式复杂、施工步骤较多的桥梁结构，大多采用有限元逐步增量法。

目前，在设计过程中，由于商业软件较为发达，以Midas Civil为代表的桥梁结构有限元软件，已成为设计人员从事桥梁设计的必备工具。实践工程中，Midas Civil设计的桥梁在最近十几年时间内，也经受住了考验。因此，在研究徐变算法时，以与Midas Civil的计算对比结果为基准，但Midas Civil并未给出详细具体的计算算法，只能从其仅有的帮助文件或相关手册内容进行研究，来论证可能的徐变计算方法。

下面分别对Midas Civil给出的徐变计算模型和常见的基于Tröst-Bazant方法给出的工程实用分析基本方程的逻辑关系进行论证。并基于论证结果，给出具体的徐变计算算法。

2.1 Midas Civil相关算法研究

在Midas Civil的帮助文件及相关技术手册中，该软件给出了混凝土的应变方程，即

ε(t)=εe(t)+εc(t)

(4)

式中，ε(t)为混凝土总应变；εe(t)为混凝土弹性应变；εc(t)为混凝土徐变应变；t为徐变计算时刻。

当Midas Civil采用徐变系数计算方法时，其混凝土的徐变应变表达式为

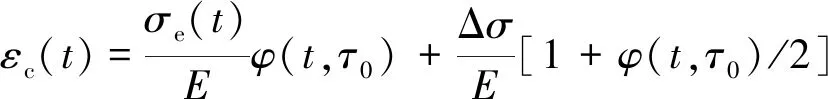
(5)

式中，σe(t)为混凝土加载的初始应力；Δσ为每一个加载持续时间段内的应力增量；E为混凝土弹性模量；φ(t，τ0)为徐变系数；τ0为混凝土的加载龄期。

式(4)、式(5)是Midas Civil中混凝土材料徐变计算中应力应变增量关系，以这两个表达式为基础，将其转换成全量形式，过程如下。

由式(4)可写出对应的应力表达式

σ(t)=σe(t)+Δσ

(6)

式中，σ(t)为混凝土计算时刻的总应力；Δσ为每一个加载持续时间段内的应力增量。

联立方程(4)～(6)可得

[1+φ(t，τ0)/2]

(7)

对式(7)进行展开，由此可得

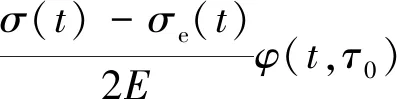
(8)

由于σe(t)=E×εe(t)，对式(8)进行整理可得

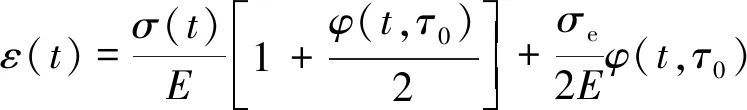
(9)

对式(9)两边同乘E并移项，可得

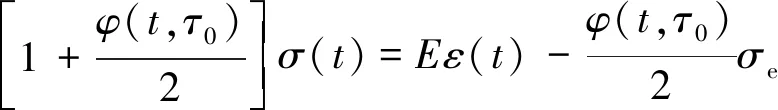
(10)

该表达式即为从Midas Civil的帮助文件给出的混凝土应变方程出发，得到的混凝土徐变应力应变全量关系表达式。

将式(10)代入伽辽金平衡弱解方程，即可利用相关的弱解方程求解工具进行求解。

伽辽金平衡弱解方程的通式为

(σ;δε)=(f;δu)

(11)

将式(10)代入后可得

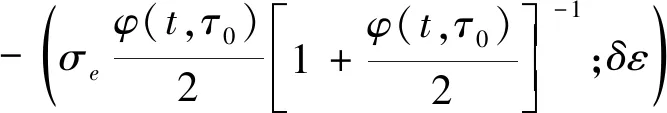
(12)

2.2 基于Tröst-Bazant的工程实用分析算法研究

在国内外可查询的相关资料中，混凝土徐变的应力-应变方程一般表述为

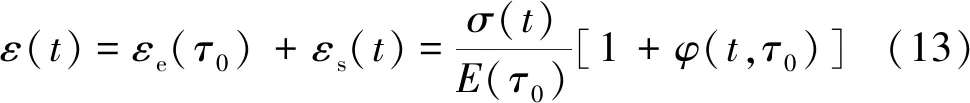
式中，ε(t)、σ(t)分别为混凝土计算时刻的总应变和总应力；E(τ0)为混凝土弹性模量；φ(t，τ0)为徐变系数；εe(τ0)为弹性应变；εs(t)为徐变应变；τ0为加载龄期；t为徐变计算时刻。

采用Tröst-Bazant方法给出的工程实用分析基本方程为

(14)

式中，εs(t)为徐变应变；σs(t)为徐变应力；σ(τ0)为弹性应力；E为弹性模量；φ(t，τ0)为徐变系数；ρ(t，τ0)为老化系数。

下面以式(13)、式(14)为基础，推导出对应的混凝土徐变应力应变全量关系表达式。

全量形式的徐变应变和徐变应力可表示为

(15)

将式(15)代入Tröst-Bazant基本方程(14)可得

[1+ρ(t，τ0)φ(t，τ0)]

(16)

对式(16)两边进行整理可得

(17)

对式(17)两边同乘E并移项，可得

[1+ρ(t，τ0)φ(t，τ0)]σ(t)=Eε(t)-

σ(τ0)φ(t，τ0)[1-ρ(t，τ0)]

(18)

同理将式(18)代入伽辽金平衡弱解方程的通式(σ;δε)=(f;δu)，可得

([1+ρ(t，τ0)φ(t，τ0)]-1Eε(t);δε)=(f;δu)+

-(σ(τ0)φ(t，τ0)[1-ρ(t，τ0)]×

[1+ρ(t，τ0)φ(t，τ0)]-1;δε)

(19)

对比式(12)和式(19)可知，这两个表达式只要满足ρ(t，τ0)=1/2时，其方程是等价的。

因此，徐变计算要取得与Midas Civil一致的结果，只需按照基于Tröst-Bazant基本方程推导而来的计算方法即可。

3 徐变的增量递推算法

基于Tröst-Bazant基本方程的徐变算法，国内相关学者[21]已进行较多研究，下面根据相关文献总结出桥梁结构基于空间梁单元的徐变计算增量算法。

3.1 各子步徐变位移表达式

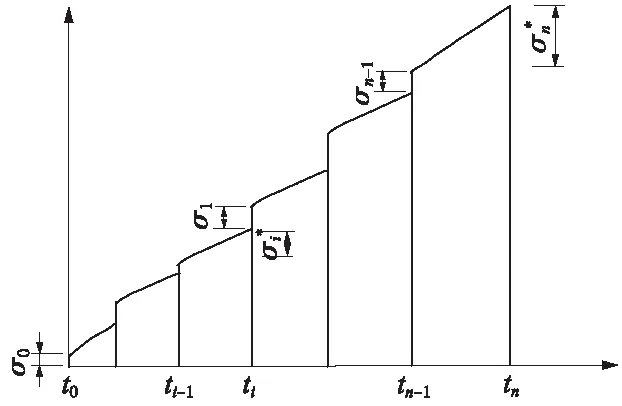
图1 徐变计算应力与时间的关系

根据徐变的定义，时刻tn的徐变应变可表示为

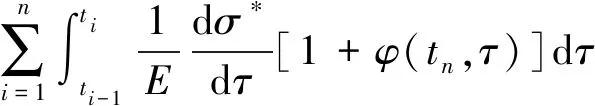
(20)

时刻tn-1的徐变应变为

(21)

利用积分中值定理，可得第n个阶段即tn-1→tn的徐变应变为

式中相关变量的表达式为

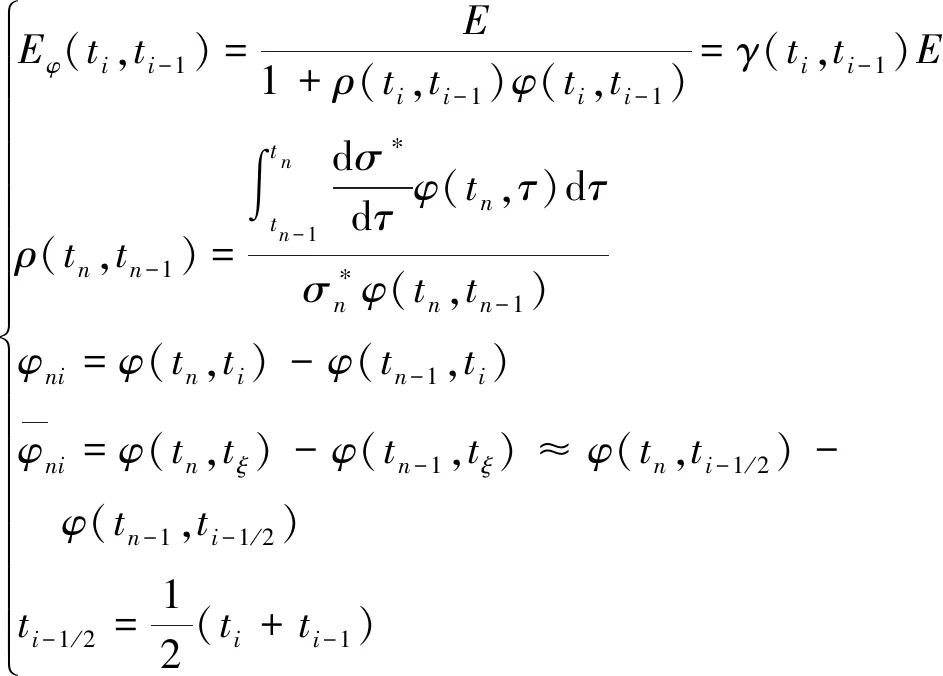
(23)

式中，γ(ti，ti-1)=1/[1+ρ(ti，ti-1)φ(ti，ti-1)]。

另外，根据虚功原理和Castigliano第一定理，可得到如下表达式

{F}=γ(t，τ0)[K]{δ}-γ(t，τ0)φ(t，τ0){F0}=

γ(t，τ0)[K]{δ}-γ(t，τ0)φ(t，τ0)[K]{δ0}=

[Kφ][{δ}-φ(t，τ0){δ0}]=

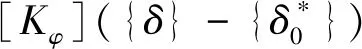
(24)

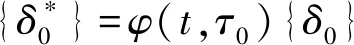
将上述平衡方程与式(20)结合，可得第n阶段(tn-1→tn时段)的徐变位移为

(25)

式中，弹性位移{δ0i}由初始阶段的位移法分析得到；总徐变位移{δi}由结构总体平衡方程解出。

3.2 徐变计算的递推公式

直接利用式(25)来计算徐变位移并不方便，因为每一步都需存储前一阶段的中间参数{δ0i}、{δi}等参数，因此，需结合徐变系数构造一个递推格式，以便快速计算徐变效应。

设徐变系数的通用公式为

(26)

式中，βa(τ)、βd(0)为徐变系数拟合时与初始时刻0、加载时刻τ有关的拟合系数；Ci(τ)为Dirichlet级数展开时与加载时刻τ相关的徐变系数形状系数；qi为Dirichlet级数展开时与随时间变化的徐变系数曲线形状相关的系数。

弹性位移{δ0i}由初始阶段位移法分析得到，总徐变位移{δi}由结构总体平衡方程解出。

将式(26)代入上述各表达式，并定义如下变量

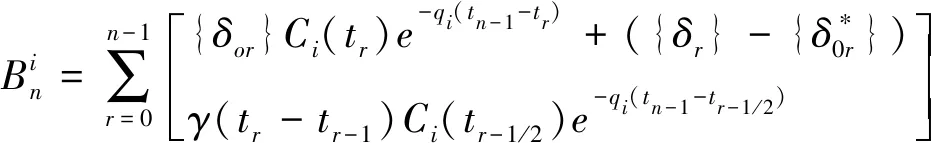
(27)

则第n阶段(tn-1→tn时段)的徐变位移表达式可表示为

{δ0n-1}[βa(tn-1)+βd(0)]

(28)

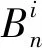
γ(tn-tn-1)Ci(tn-1/2)e-qi(tn-tn-1/2)

(29)

因此，徐变计算表达式即可用式(28)、式(29)对应的递推公式表示。

接下来，只需将本文所述的公路规范和铁路规范的徐变系数拟合成式(26)所示的通用表达格式，即可自动处理不同规范的徐变计算问题。

对于自定义的徐变系数，可通过如下加权最小二乘法进行拟合，加权最小二乘的格式如下

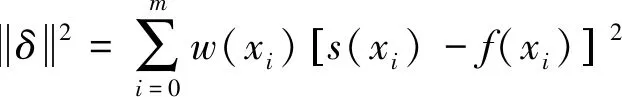
(30)

式中，w(xi)为加权值；s(xi)、f(xi)分别为拟合点处的拟合值及规范计算值。

3.3 徐变递推计算基本步骤

在进行徐变效应分析时，可按以下3个步骤分别进行分析。

第一步：对徐变系数进行拟合。

式(2)、式(3)分别展示了公路和铁路规范的徐变系数，但程序计算时，不能用该表达式进行计算，均需将其转化为式(26)的公式。因此，本阶段的主要任务即为用加权二乘法对徐变系数进行处理。

第二步：对n=1阶段进行处理，主要按如下过程进行处理。

(1)计算初始阶段的弹性变形。

(5)组集总刚和荷载列阵，列出总体平衡方程式，处理边界条件后解出{δ1}。

(6)计算徐变引起的总杆端力[F1]和约束反力。

第三步：对n=2以后的阶段进行递推计算处理，主要按如下过程进行处理。

(1)计算现阶段的弹性变形{δ01}。

(5)组集总刚和荷载列阵，列出总体平衡方程式，处理边界条件后解出{δ2}。

(6)计算徐变引起的总杆端力[F2]和约束反力。

(7)继续循环进入下一阶段计算。

按照上述3个步骤，即可编制有限元程序，进行徐变位移计算。

最终的徐变位移需将每一施工阶段计算得到的位移增量进行叠加。计算中，遇到体系转化，只需将由此导致的二次力叠加入下一个阶段即可。

笔者在研制自主有限元软件“卧龙”时，按照上述计算方法和过程进行了徐变计算的探索，并对其结果的准确性进行了案例测试。下面给出基于上述算法的“卧龙”与Midas Civil的验证案例。

4 徐变位移计算程序验证

某三跨连续梁，梁跨组合为94.5 m+166.4 m+107.9 m，总梁长368.8 m。同时模拟桩基础、承台、墩身的施工过程，其对应混凝土为C40、C30混凝土，这部分混凝土不考虑收缩徐变效应。梁体采用C60混凝土并考虑收缩徐变效应，梁体截面为单箱单室截面。钢束采用Strand1860，钢束特性值有3组，钢束数量有238组，施工阶段共分40个阶段。静力荷载包括自重、挂篮、钢束张拉力、二期恒载等，其计算模型如图2所示。

图2 三跨连续梁测试模型

测试过程，徐变系数采用《2018年公路规范》提供的徐变系数表达式。

采用“卧龙”与Midas Civil背靠背对比计算模式。计算过程中，考虑了钢束的二次力、钢束引起的截面特性变化影响，也考虑了梁体变截面的影响。由于施工阶段比较多，限于篇幅，直接选取成桥后10年的数据进行对比。

分别提取两个软件的徐变位移，数据如表1所示，由于空间梁单元的每个节点有6个自由度，但对于连续梁来说，其主要受力为自重及钢束，因此，可选取竖向和水平两个方向的徐变位移作为对比自由度。由于全桥节点较多，下面仅选取第29～51号单元进行比较，这些单元代表了中跨靠近第一个桥墩这半个跨度的桥梁结构，具有典型性。

表1给出了“卧龙”与Midas Civil在竖向和水平向两个方向的徐变位移对比结果。表中，Dzm、Dxm分别为Midas Civil计算的竖向和水平向徐变位移；Dzw、Dxw分别为卧龙计算的竖向和水平向徐变位移。从表1中可以看出，竖向徐变位移的最大误差为3.3%，该节点号为29号，位于第一个主墩节点上。该节点的徐变位移为上拱状态，与其余节点的徐变位移方向相反，相对来说，该点徐变绝对值较小。中跨跨中位置节点号为51号，其相对误差为1.19%。所有节点的水平向徐变位移，其误差都在1%以内。

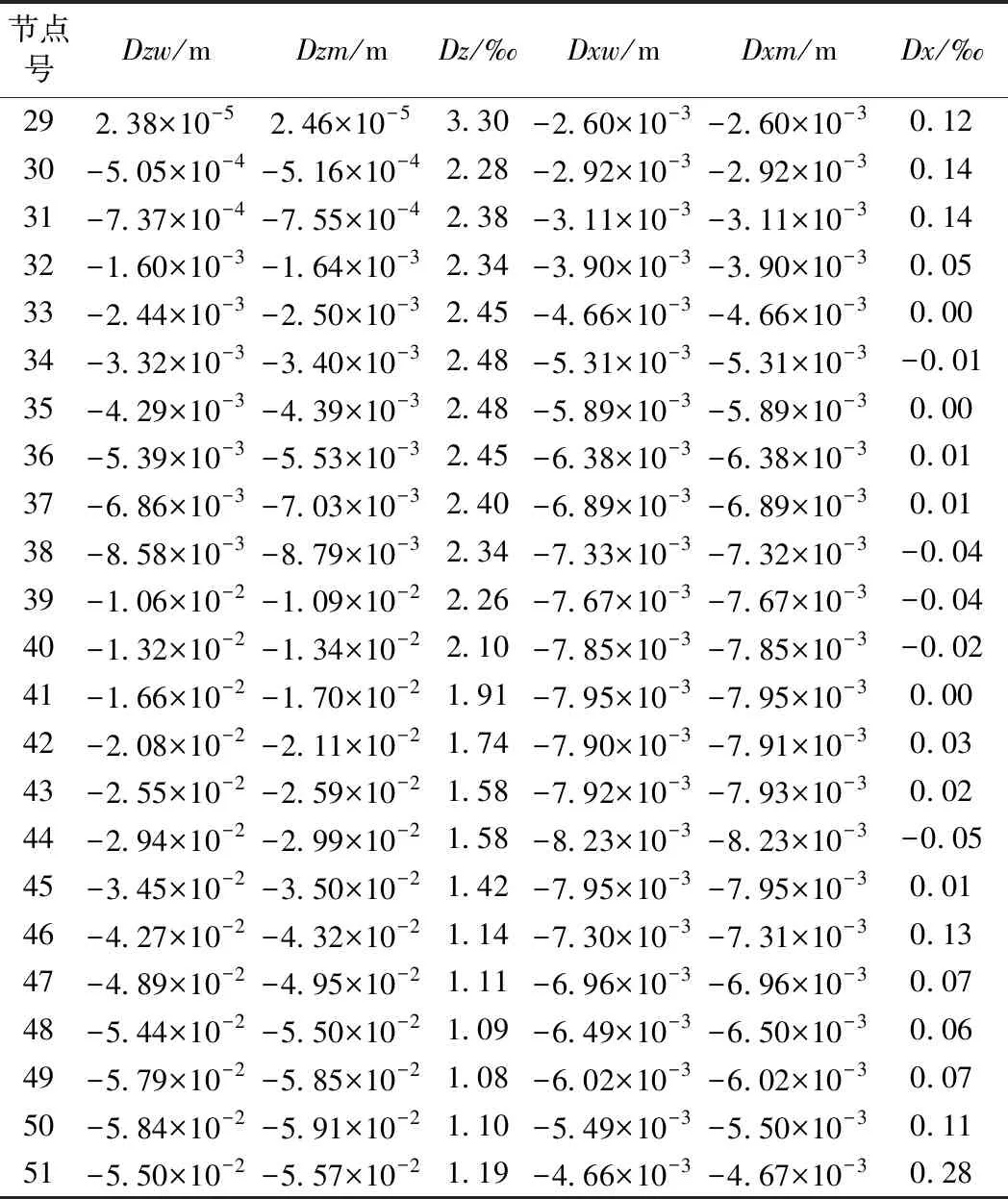
表1 自编程序卧龙与Midas的徐变位移对比

将表中两个方向的徐变计算值分别绘制成对比图，如图3所示。

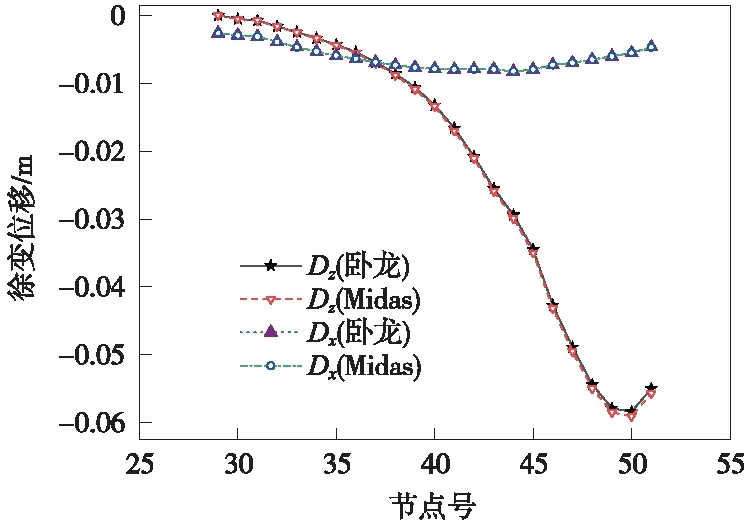
图3 徐变位移值对比

从图3中也可以看出，不论是竖向徐变位移值还是水平向徐变位移值，“卧龙”和Midas Civil的结果都是非常相近的。

“卧龙”与Midas存在误差的原因为：采用递推格式时，需对徐变系数进行拟合，其拟合数值和规范表达式计算出的精准数值是存在误差的；Midas的徐变系数计算值与规范精准值之间也会存在误差。但总体来看，“卧龙”与Midas Civil之间的误差是可以接受的，这也表明，上述基于递推形式的徐变计算方法是可行的。

5 结论

通过系统梳理徐变系数的相关规定，给出了现行公路和铁路规范的相关规定。针对Midas和基于Tröst-Bazant基本方程的两种徐变算法，对其进行全量形式的公式推导和对比分析。随后，给出递推形式的徐变计算方法及计算步骤，并通过一个较为复杂的连续梁案例进行测试，结论如下。

(1)现行铁路规范和公路规范的徐变系数表达式区别很大，可通过加权最小二乘法将其转化成徐变系数设定的通用格式，从而统一徐变计算过程。

(2)Midas帮助文件给出的徐变算法和基于Tröst-Bazant基本方程的徐变算法本质上是一致的。当满足ρ(t，τ0)=1/2时，两者之间的方程是等价的。

(3)将徐变系数写成设定的通用格式，可将基于空间梁单元的徐变算法改造成递推形式，递推形式的徐变计算过程将大大减少运算量和数据存储量，加快运算速度。

(4)实例测试结果表明，在充分考虑钢束二次力、结构体系转化影响、变截面性质及钢束引起的截面特性变化情况下，本文所述徐变算法计算得到的徐变位移和Midas计算得到的徐变位移结果非常接近。

(5)测试结果表明，自编程序“卧龙”的徐变计算精度，在成桥后10年，竖向徐变位移的最大误差为3.3%，且徐变绝对值较小，水平向徐变位移误差均在1%以内，计算精度良好。