定位式作业客运站调机运用优化模型研究

吕红霞, 倪少权, 陈钉均

1.西南交通大学 交通运输与物流学院，四川 成都 610031;2.西南交通大学 全国铁路列车运行图编制研发培训中心，四川 成都 610031；3.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

调机运用计划是铁路客运站作业计划的重要组成部分,其核心是确定始发、终到旅客列车车底出入库时间及次序、调机运用及整备计划。其中车底出入库作业时间决定了始发、终到列车占用到发线、客技线的起止时间。所以，调机作业计划是协调客运站各子系统作业的重要作业，起着牵一发而动全身的作用。

目前调机运用优化的研究集中在编组站和区段站，对客运站调机运用计划的研究尚属起步。国外对调机的研究起源于20世纪50年代，主要是通过对调车场调车的优化，提高铁路货物运输的有效性和可靠性[1-5]。文献[6]将技术站调机问题转化为偏序集合的全序分解问题，利用偶图最大匹配问题的方法解决调机运用问题。文献[7]采用划分时间片方式构造调机运用的加权无向图模型，采用模拟退火算法，求出调机使用的计划安排。文献[8]建立了编组站调机运用单机调度模型，并设计蚁群算法。文献[9]对拥有大型货场和大量专用线编组站取送调机的作业组织优化问题进行了分析，在分析各作业占用取送调机时间的基础上,采用图论法对有时间窗的问题进行了求解。文献[10]以最小化延迟解体列车和编组列车加权数量为目标建立数学模型，以解编顺序作为优化对象，设计禁忌搜索算法对其进行求解。

国内外对车站作业计划优化技术和方法的研究长期集中在编组站领域。而编组站技术作业内容与客运站有着很大不同,编组站调机主要解决车流分配，调机优化基于车流推算；而客运站调机主要解决车底出入库，调机优化主要是确定车底出入库时间及其牵引调机。 由于我国既有线大多数的客运站为定位式作业客运站，本文研究定位式作业客运站调机运用优化问题。

1 问题描述

调机运用计划问题应遵循以下条件：

(1)一台调机在同一时间内只能进行一项作业；一项作业一旦占用了一台调机便一直占用到作业完毕时为止，中间不能中断为其他作业服务，一项作业只能使用一台调机。

(2)每项待安排作业均有适当的调机承担，并满足调机的使用方案。

(3)满足列车在站的各项作业时间标准。包括满足车底在客技线上的客检、库整作业时间标准，列车在到发线上的终到、始发作业时间标准，行调作业咽喉走行时间标准和调机各项作业时间标准。

(4)调车作业与行车作业、调车作业与调车作业之间可以平行进行，保证各项作业进路无干扰。

在满足上述条件下,实现下述目标：

(1)调机总走行距离短，避免不必要的空行程(不牵引车底的行程)。

(2)有效利用客运站的设备，对现有的车站设备应尽量均衡利用，使各项设备的利用率趋于均衡，在本文中指调机作业均衡。

(3)保证车站各作业子系统协调作业。

2 客运站调机运用计划优化模型的建立

2.1 参数设置

变量βij表示送车底作业Ji(Ji∈Js)与取车底作业Jj(Jj∈Js)是否满足取送车底作业合并条件。βij=1表示送车底作业Ji与取车底作业Jj满足合并条件，βij=0表示送车底作业Ji与取车底作业Jj不满足合并条件。

变量αij表示调机任务Ji与调机dj的适应度，αij=1表示调机dj可以承担任务Ji，αij=0表示调机dj不能承担任务Ji。

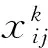
决策变量sti，eti表示Ji的开始时间和结束时间；ti为Ji的作业时间长度，ti=eti-sti。

ND为可用到发线数，设NK为可用客技线数，Td为调机的等待时间。

2.2 目标函数

①取送车底作业的空走程数最少

该目标可以转化为成组取送车底作业数最多，可以表示为

( 1 )

②调机均衡作业

所有调机任务需要的总调机作业时间为

( 2 )

则在本计划编制阶段调机的平均作业时间为

( 3 )

调机j的总作业时间与平均作业时间的差可以描述为

( 4 )

minZ2=Δtmax

( 5 )

当Δtmax最小时，即到达了均衡使用调机的目的。

③客运站各子系统协调作业

由于旅客列车的始发tc、终到时间tz均是确定的，并且调机数目是固定的，而调机的取送车底作业时间标准，即调机的有效作业时间是确定的，因此，调机的等待时间(空费时间)Td也是固定的。调机取送车底计划确定了列车占用到发线、客技线的起止时间，直接影响着客运站的到发线、客技线运用，是协调各个子系统作业的重要因素。在实际生产中，车站生产指挥人员通常通过调整列车出入库时间来协调到发线、客技线、牵出线和咽喉的作业。例如，当到发线能力紧张时，站调会组织列车早入库、晚出库。当客技线能力紧张时，站调会组织列车晚入库、早出库。因此在安排客运站的调机运用计划时，不仅要考虑调机计划本身的优化问题，还要通过调机计划协调到发线、客技线的运用，使全站各子系统协调作业。在编制调机运用计划时，根据调机作业时间确定的同时使用到发线、客技线的列车越少，列车在到发线和客技线上作业的时间干扰越少，就越有利于到发线和客技线运用计划的编制。因此，以同时占用到发线、客技线列车数最小为目标。

( 6 )

式中：α、β表示权重系数，α≥0,β≤1。

2.3 约束条件

① 每项作业必须且只能安排一台适当的调机承担

( 7 )

( 8 )

( 9 )

(10)

(11)

② 在同一时刻每台调机只能承担一项作业

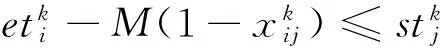
(12)

③ 满足车站各项作业时间标准的要求

满足列车、车底在站各项作业时间标准的要求，即调机作业起时间应在其作业时间窗口内。

(13)

取送车底作业满足取送车作业时间标准。

(14)

(15)

④ 咽喉作业协调

对于取送车底进路与列车到发进路有交叉的车站来说，在安排调机作业时应在时间上避开与接发车进路的干扰、减少调车作业之间的干扰。咽喉作业协调可以描述为。

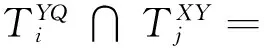
(16)

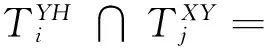
(17)

⑤ 成组取送作业满足取、送车底作业结合条件，且只能结合一次

(18)

(19)

(20)

⑥ 牵出线(走行线)作业协调

在定位式作业的车站上，在客技场和到发场间一般有走行线或牵出线连接，取送车底作业均需从牵出线上经过。因此在确定取送车底作业的时间应考虑该作业占用牵出线(走行线)的时间，使各项作业占用牵出线的时间不冲突。牵出线(走行线)作业协调可以描述为

(21)

⑦ 到发线、客技线作业协调

在确定调机取送车底作业时间时，可以实时地测算到发线、客技线的能力，当发现某一时刻需要占用到发线的列车数大于可用到发线数、需要占用客技线的列车数大于可用客技线数时，说明将无法编制到发线、客技线运用计划，该项作业安排的时间不合适，需要调整。因此调机作业应为到发线、客技线子系统协调作业创造条件可以描述为在同一时刻占用到发线、客技线作业的列车数最少，且小于可用的到发线数、客技线数，为合理、均衡使用到发线和客技线创造条件。

(22)

(23)

3 模型的分解

3.1 模型1：取送车底成组作业方案模型

将尽可能地组织成组作业的目标从原问题中抽出，可以描述为以下数学模型

(24)

s.t.

βij-yij≥0 ∀i,j

(25)

(26)

(27)

式中决策变量yij为0-1变量，yij=1，表示第i项取车作业与第j项送车作业合并为取送车作业。

该问题的图论模型描述如图1所示。

图1 成组作业方案图论模型

因此成组取送车作业的作业方案，可以转化为一个分配问题。在确定取送车成组作业方案时，应尽量使取送车作业结合后的时间窗口最大。

(1)尽可能多地组织成组作业，即取车作业和配车作业配对数最多；

(2)成组作业的时间窗口尽可能大。

在进行模型求解时首先考虑第一个目标，在第一个目标求解结果基础上，再将第二个目标加入到模型中，得到模型

(28)

(29)

(30)

(31)

(32)

对模型进行如下改进，将其转化为标准的指派问题。

(1)对取车底作业与送车底作业数不等的问题，增加虚拟的取车底作业或送车底作业，使之成为任务数和资源数相等的指派问题。

(2)建立n阶权值矩阵Cn×n，n=max(Jqc,Jsc)。将目标1和目标2加权为一个目标。

(33)

式中:max_tw=max(twij)，∀i,∀j，M为一个大正数。

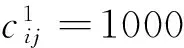
(34)

(35)

(36)

该模型是标准的指派问题模型。

3.2 模型2：确定调机作业顺序模型

调机作业顺序优化问题，主要确定每台调机的作业顺序，为每一个调机作业任务分配一个合适的调机，并保证调机均衡作业。描述为以下数学模型

minZ2=Δtmax

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

3.3 模型3：确定调机作业时间模型

调机作业时间模型根据与调机作业进路有交叉的行车作业的咽喉占用时间、牵出线作业时间以及到发线、客技线的能力，确定各项作业占用调机的起止时间，避免行调作业干扰、牵出线作业冲突，并使同时使用到发线、客技线的作业数最少，为合理使用到发线、客技线创造条件。

(45)

(46)

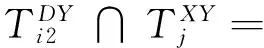
(47)

(48)

(49)

(50)

(51)

(52)

4 调机运用计划多层决策模型及算法

将调机运用优化模型分解后，原模型转化为求解以上三个子模型，基于分层序列法建立调机运用计划多层决策模型(图2)，该模型包含三个层次，分别对应这三个子模型。顶层解决调机运用的成组作业方案问题，保证调机作业的空行程最少。中层确定各台调机作业顺序，保证每项任务都分配了适当调机的情况下，调机能够均衡作业。底层确定调机作业的起止时间，保证车站各子系统间协调作业，牵出线、咽喉作业不冲突。这三个子模型是相互联系、不可分割的。编制计划时可能需要对方案进行评价，查看是否可以调整调机、到发线、客技线计划，若可以调整，则对计划进行调整，然后继续编制客运站计划；否则，将当前编制的结果显示给用户，使用户对编制结果进行调整，然后系统在用户调整的结果上，获取未安排的行车、调车任务，再继续编制计划，直到编制完毕为止。

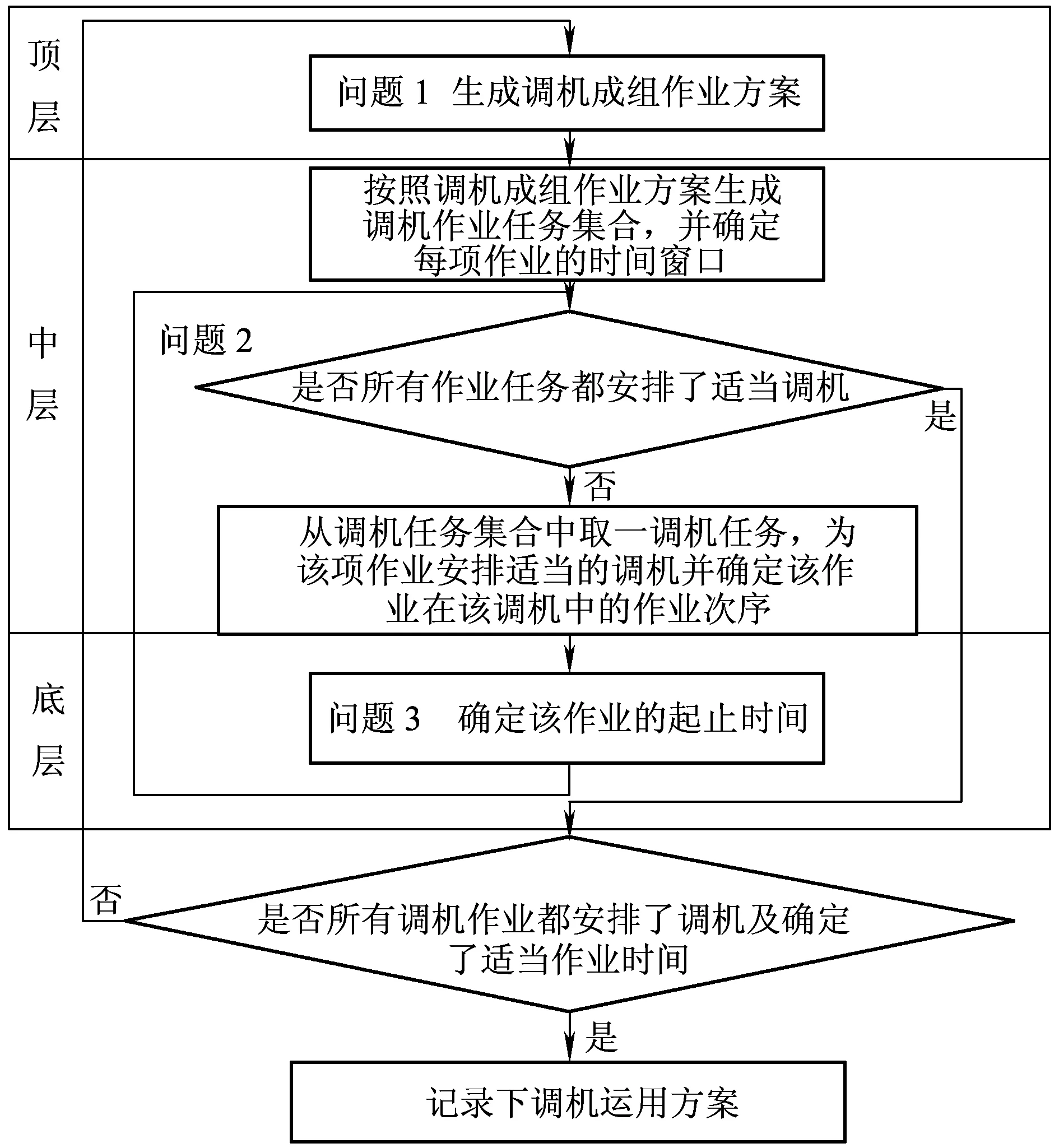
图2 调机作业计划多层决策模型

针对调机作业计划多层决策模型的特点，设计了定位式客运站调机作业计划的多层蚁群优化算法，由于篇幅原因，另文介绍。该算法包括三个层次，上层是将成组作业方案优化问题转化为标准分配问题，提出了基于分枝定界算法和蚁群算法的调机成组作业方案求解算法；中层为将调机作业顺序模型转化为车辆数固定的、带时间窗口的车辆路径问题，并采用蚁群算法设计了求解算法；底层为在考虑调机作业、到发线、客技线、牵出线、咽喉协调作业的基础上，设计了调机作业时间优化算法。当采用匈牙利法结合分枝定界法求得调机成组作业方案的多个最优解，但对每一个调机成组作业方案都无法求得调机作业顺序和调机作业时间的可行解时，可以根据确定性寻优阶段的经验，采用蚁群算法对调机成组作业方案问题进行求解，对每次迭代的构造解继续求解调机作业顺序及安排调机作业时间，并根据其结果更新信息素矩阵。

5 系统及算例

依据建立的模型和算法，研发了大型客运站行车调度辅助决策系统(图3)，该系统已经在成都客运站、哈尔滨客运站、沈阳客运站等投入运用，取得了良好的效果。以成都客运站实际数据为例，该站具有3台调机，该站的调机作业计划见表1。

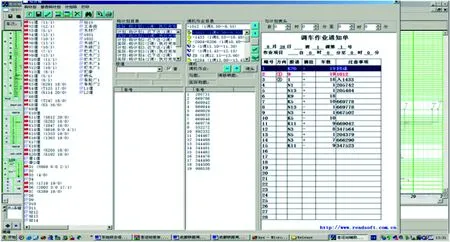
图3 调车作业计划的编制界面

表1第1调机作业计划表

调机顺序作业车底号起止记事D11取车底73928001918.1618.40+K452D12取车底76029002017.5118.16+K698D13出入库作业72430000518.4019.10-T7+T22D14交接班125117002819.1119.41JD15送车底124918002919.4120.15-07420D16出入库作业76931000320.1520.45-K291+N781D17站整126319003020.4521.00ZD18送车底73231000621.0021.25-N757D19出入库作业74231000721.2521.55-7403+K191D110取车底75031002121.5522.20+N745D111站整121519003122.2022.59ZD112送车底75331002222.5923.24-K245D113站整122520003223.241.00Z…………………D140站整121640002516.1516.45ZD141取车底74127000116.4517.10+K386D142送车底125236001517.1017.35-K192D21交接班122917001318.1619.01JD22取车底72029000318.5919.24+K678D23取车底72729001719.3020.00+K424D24站整122319001420.0020.10ZD25出入库作业76531000220.1020.45-T895+K246

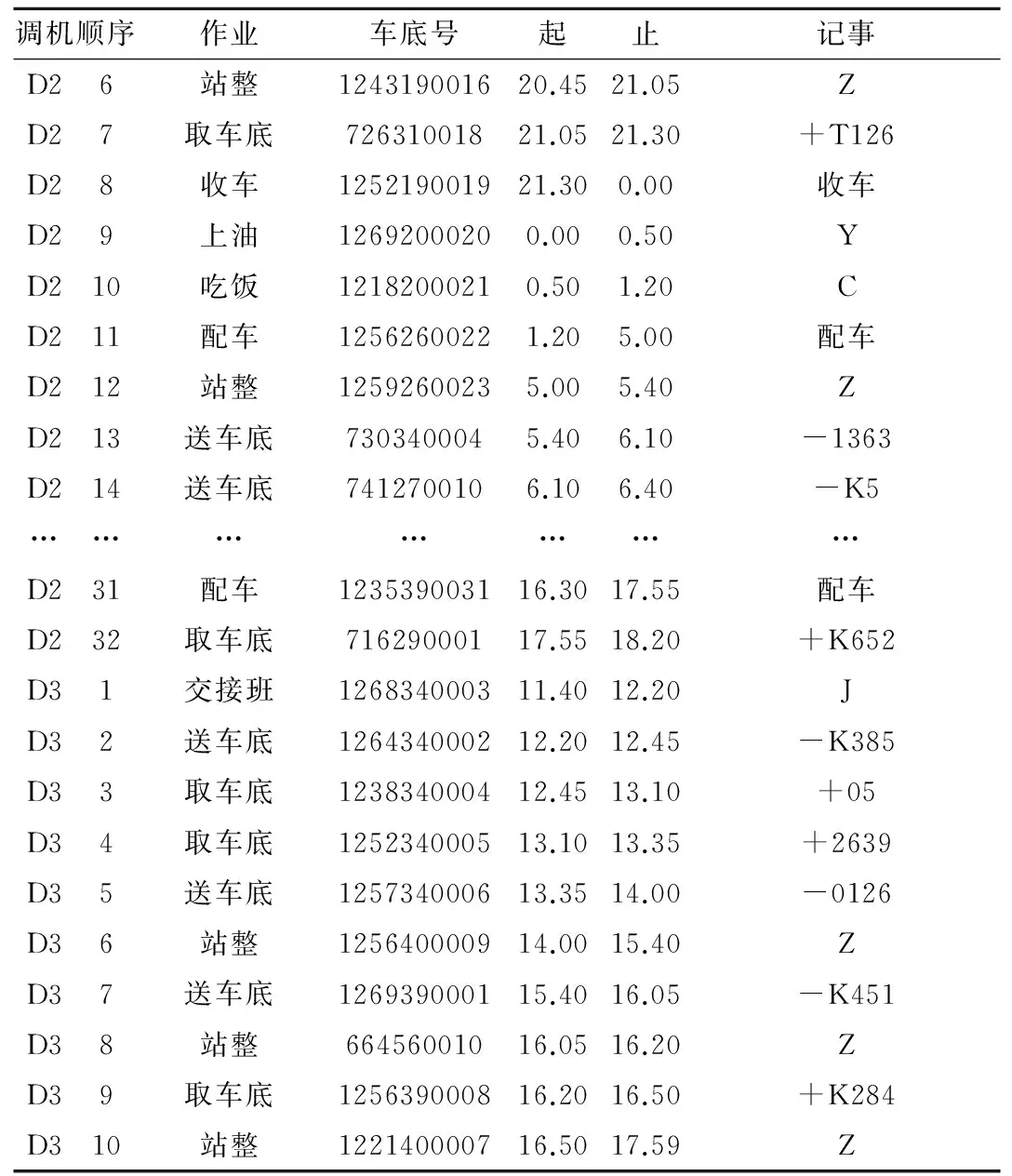
续上表

6 结束语

客运站调机运用优化是客运站作业整体优化的关键，起着牵一发而动全身的作用。本文对定位式作业客运站的调机运用问题进行了详细分析，提出了客运站作业协调定量化描述的方法，在此基础上，建立了该问题的多目标、约束复杂、混合0-1规划模型。为便于求解，将其分解为成组作业方案优化、调机作业顺序优化、调机作业时间优化三个子模型，采用分层序列法建立了客运站调机作业运用优化的多层决策模型。

在对模型进行分析的基础上，提出了定位式客运站调机作业计划的多层蚁群优化算法。将成组作业方案优化问题转化为标准分配问题，提出了基于分枝限界算法和蚁群算法的调机成组作业方案求解算法；将调机作业顺序模型转化为车辆数固定的、带时间窗口的车辆路径问题，采用蚁群算法设计了求解算法；为了满足调机、到发线、客技线、牵出线、咽喉协调作业的要求，设计了调机作业时间优化算法。

本文根据列车运行图规定的始发终到列车的发、到时刻和作业时间标准编制调机取送作业方案。实际上，列车偏离运行图的情况时有发生，如何编制能够较好适应列车各种随机变化的调机运用方案，亦即采用随机规划方法编制调机取送作业方案是需要进一步研究的内容。本文将整个模型分解为三个模型进行求解的方法，降低了问题求解难度，但是客运站调机运用优化本身是一个多影响因素、多目标、半结构化决策问题，如何更好的设计算法，求解模型也是下一步需要研究的工作。

参考文献：

[1]Dieter A， Hiller. Properties of Urbic Anthrosols from an Abandoned Shunting Yard in the Ruhr Area, Germany[J]. Catena. 2000,(39):245-266.

[2]HANSMANN R S, ZIMMERMANN U T. Optimal Sorting of Rolling Stock at Hum Pyards[M]. //Krebs H J, Jäger W. Mathematics-Key Technology for the Future. Berlin/ Heidelberg: Springer, 2008:189-203.

[3]GATTO M, MAUE J, MIHALK M, et al. Shunting for Dummies: An Introductory Algorithmic Survey[M]. //Ahuja R, Mring R, Zaroliagis C. Robust and Online Large-scale Optimization, Lecture Notes in Computer Science, Berlin/Heidelberg:Springer, 2009,(5868):310-337.

[4]Nikbakhsh Javadian, Hamid Reza Sayarshad, Sajjad Najafi. Using Simulated Annealing for Determination of the Capacity of Yard Stations in a Railway Industry[J]. Applied Soft Computing, 2011,(11): 1899-1907.

[5]Nils Boysen, Malte Fliedner, Florian Jaehn, Erwin Pesch. Shunting Yard Operations: Theoretical Aspects and Applications[J]. European Journal of Operational Research, 2012, (220) :1-14.

[6]李文权,王炜,杜文,等.铁路技术站调机运用模型及算法[J].系统工程学报，2000,15(1):38-43.

LI Wen-quan, WANG Wei, DU Wen, et al. The Model and Algorithm of Using Shunting Engines for Railroad Technical Service Station[J]. Journal of Systems Engineering, 2000,15(1):38-43.

[7]徐杰,杜文,李宗平,等.基于模拟退火算法合图着色的调车机车安排研究[J].铁道学报，2003,25(3):25-30.

XU Jie, DU Wen, LI Zong-ping, et al. Study on the Plan of Using Shunting Locomotives Based on Simulated Anncaling Algorithm and Graph Coloring[J]. Journal of the China Railway Society, 2003,25(3):25-30.

[8]王世东,郑力,张智海,等.蚁群算法在调机运用计划中的应用[J].中国铁道科学，2007,28(3):104-109.

WANG Shi-dong, ZHENG Li, ZHANG Zhi-hai, et al. Solving the Scheduling Problem of Hump Locomotive with Ant Colony Optimization[J]. China Railway Science, 2007,28(3):104-109.

[9]赵小柠.基于时间窗的大型编组站取送调机作业优化研究[J].兰州交通大学学报,2008,7(1):76-79.

ZHAO Xiao-ning. Research on the Optimization of Shunting Engine Operation in Large Marshalling Station Based on Time Window[J]. Journal of Lanzhou Jiaotong University, 2008,7(1):76-79.

[10]王烁,何世伟,黎浩东,等.禁忌搜索算法在编组站调机运用计划中的应用[J].铁道运输与经济，2011,33(2):83-87.

WANG Shuo, HE Shi-wei, LI Hao-dong, et al. Application of Tabu Search Algorithm on the Scheduling Problem of Shunting Locomotive[J]. Railway Transport and Economy, 2011,33(2):83-87.