面向到达间隔时间压缩的高速铁路车站到发线运用优化研究
潘明轩,宁 佳,鲁工圆,3,王超宇,敬亭婷
(1.成都设计咨询集团 成都市交通发展研究院,四川 成都 610000;2.西南交通大学 交通运输与物流学院,四川 成都 610031;3.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031;4.广州地铁设计研究院股份有限公司 交通规划所,广东 广州 510000)
0 引言
我国高速铁路建设与发展已取得傲人成绩,但是运营水平与世界先进水平尚有一定差距。以京沪高速铁路(北京南—上海虹桥)为代表的我国高速铁路到发线能力紧张问题日益凸显,尤其是在高峰时段,进路间的交叉干扰导致到发线运用方案间冲突严重,直接增大了列车的到达间隔时间。因此,如何通过优化到发线运用压缩到达间隔时间,成为众多学者关注的问题。
现有论文成果中,国内外专家学者对高速铁路车站到发线的运用优化以及列车间隔时间的压缩均有一定的研究。彭其渊等[1]通过建立双目标混合整数线性规划模型,能有效解决到发线运用问题和进路冲突疏解问题;吕红霞等[2]基于蚁群算法建立0-1 规划模型优化客运站到发线的使用,并利用两元素优化的方法进行局部搜索;李宇航[3]针对列车晚点引起的冲突传播,以及行车和调车作业干扰的问题,建立到发线多目标优化模型,并运用免疫克隆算法进行求解;彭其渊等[4]建立多智能体列车连续追踪运行仿真模型,总结最有利于压缩追踪间隔时间的到发线运用方案;刘佩[5]基于列车追踪运行时空图构建车站间隔时间集,以相邻列车时间间隔最小化为目标,建立车站间隔时间的精细化计算模型。
既有关于到发线运用优化的研究,主要以到发线均衡运用、旅客便捷性等为目标,均未以压缩到达间隔时间为研究内容;而既有关于列车到达间隔时间的相关研究,大多运用仿真分析咽喉区长度、过岔速度等因素对列车间隔时间的影响,对到发线运用的影响考虑不足,因而可面向到达间隔时间压缩建立到发线优化模型,通过实例分析评估到发线运用优化对到达间隔时间压缩的效果。
1 到发线运用对到达间隔时间影响分析
列车根据到发线运用方案确定占用的咽喉区接发车进路,而不同接发车进路解锁方式会对列车咽喉区占用的开始时刻、结束时刻以及占用时长等产生影响,进而影响到达间隔时间[6]。
以上海虹桥站高速场为例,上海虹桥站高速场站型图如图1所示。运用多智能体仿真方法,在接车进路一次解锁条件下,对除正线IX,X外的所有到发线的组合运用方案进行仿真实验,得出一次解锁方式下的到达间隔时间压缩最大不超过 10 s,分段解锁方式下的到达间隔时间压缩普遍大于30 s。可以看出,一次解锁相对于分段解锁对列车到达间隔时间压缩影响较小。基于此,设计如下仿真实验:列车进路采用分段解锁模式办理,前车出清最后关联道岔组后,调度集中控制系统可为后车办理接车进路,设列车到达作业时间为40 s,通过研究同一方向相邻列车,以总结出实现到达间隔时间最小的到发线运用规则。仿真实验得到各到发线组合方案的到达间隔时间如表1所示。

图1 上海虹桥站高速场站型图Fig.1 Map of the high speed railway yard of Shanghai Hongqiao Railway Station
对于表1中任一前车到发线,分析其到达间隔最小和最大的到发线组合方案,得到到发线组合最优/最劣方案如表2所示。
由表2可以看出,前车到发线1与后车到发线2的关联道岔有9个,对应表1中到达间隔时间为233 s;前车到发线1与后车到发线11或12的关联道岔仅4个,对应表1中到达间隔时间为197 s。同理对比其他到发线组合方案的到达间隔时间,可以得出到达间隔时间最小的到发线运用规则:在编制同方向相邻2列到达列车的到发线运用方案时,到发线组合方案对应关联道岔越少,列车到达间隔时间越短。

表1 各到发线组合方案的到达间隔时间 s Tab.1 Arrival interval of each combination of arrival–departure tracks
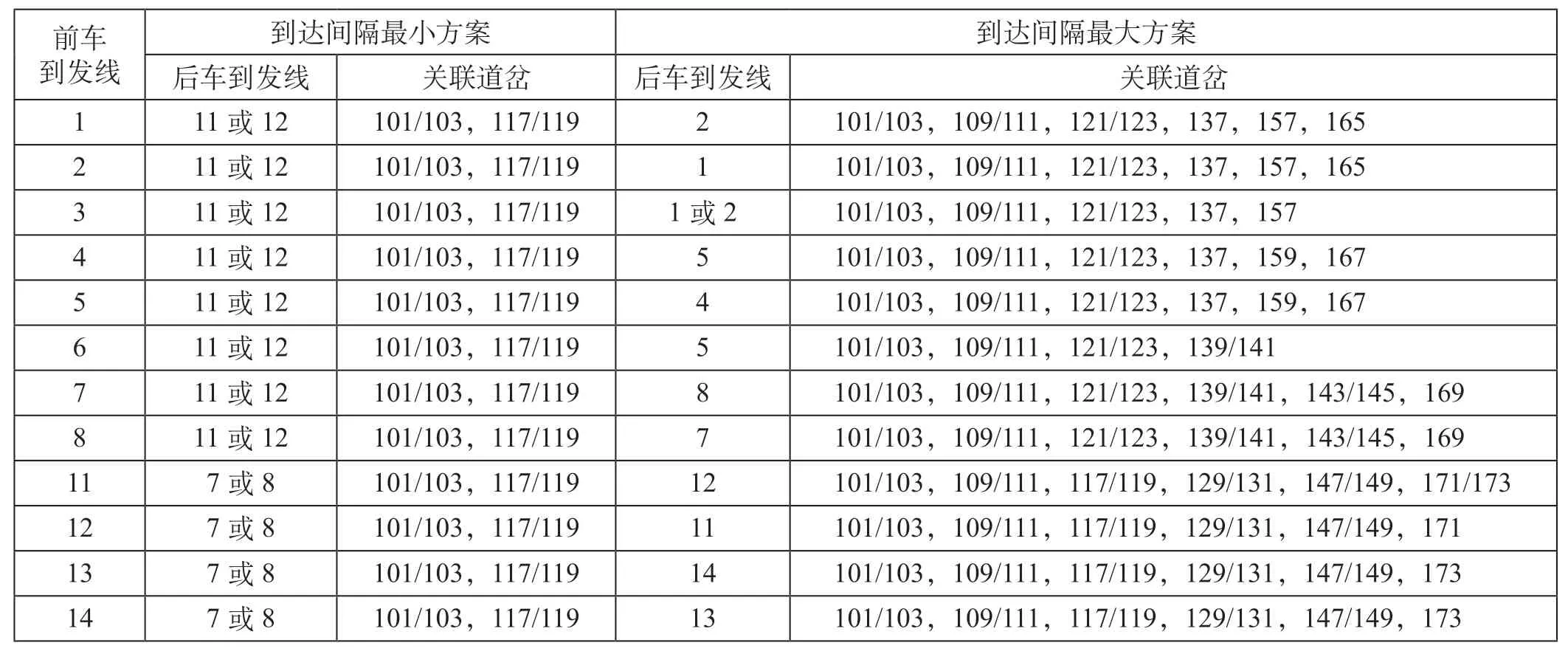
表2 到发线组合最优/最劣方案Tab.2 Best/worst combination of arrival–departure tracks
2 模型构建
高速铁路车站衔接多个运行方向,进路较为复杂,列车到达连续紧密。为了更加准确地分析该类复杂情况下到发线运用对到达间隔时间的影响,基于仿真实验及到达间隔时间最小的到发线运用规则,建立数学优化模型,分析在衔接多个运行方向的高速铁路车站内,到发线运用优化对到达间隔时间的压缩效果[7]。
2.1 列车作业重要节点描述
为方便模型构建,需对列车占用进路时间进行定义,并对部分时间节点进行处理,得到列车作业过程重要节点示意图如图2所示。
定义的列车占用进路时间有接车进路占用时间、到发线占用时间和发车进路占用时间:①接车进路占用时间表示开始为列车i办理接车进路时刻起至列车i出清接车进路时刻止的时间,其中列车出清接车进路时刻为图定到达时间,即;②到发线占用时间表示开始为列车i办理接车进路时刻起至开始为列车i办理发车进路时刻止的时间;③发车进路占用时间表示开始为列车i办理发车进路时刻起至该列车尾部出清第一离去时刻止的时间,其中列车办理发车进路时刻为图定出发时刻,即:。

图2 列车作业过程重要节点示意图Fig.2 Schematic diagram of important nodes in the train operation
定义的时间节点有:①开始为列车i办理接车进路的时刻为列车i到达车站的时刻;②列车i尾部出清发车进路的时刻为列车i离开车站的时刻。
2.2 模型变量及参数设置
设T为某一时段接发的所有列车集合,记T= {1,…,i,…,n};L为到发线集合,记L= {1,…,j,…,m};R为进路集合,记R= {1,…,r,…,p}。O为进站方向的集合,E为出站方向的集合。模型相关符号及含义如表3所示。

表3 模型相关符号及含义Tab.3 Symbols and their meanings of the model
2.3 目标函数与约束条件
模型目标函数为所有列车最晚离开车站时刻与最早到达车站时刻之差的最小值,即所有列车无缓冲时间地紧凑到达,等价于求解车站完成所有列车任务需要的最小总运营时间,总运营时间越小,越能实现更小的列车到达间隔[8],目标函数计算公式为

模型根据不同变量设置可以实现2个目标: ①将到发线选择变量和进路选择变量设为参数,仅以列车到发时间、进路占用时间为变量,以图定到发线运用方案为输入,可以求解得到该方案下完成给定列车运行任务的最小总运营时间,最小运营时间与实际运营时间之差反映图定方案的列车缓冲时间的总体情况;②将到发线选择变量、进路选择变量、列车到发时间、进路占用时间均设为变量,不固定到发线运用方案,此时模型可求解出使车站总运营时间最小的到发线运用方案,该种情况下的最小运营时间与目标①中的最小运营时间差越大,越可能实现较小的列车到达间隔。
模型需满足到发线占用唯一性、到发线接车时间间隔、进路占用相容性等约束条件,约束条件具体如下。
(1)列车作业重要时间节点关系,可表示为

(2)压缩后到达(出发)时刻不得晚于图定到达(出发)时刻,可表示为

(3)压缩后到达时刻不早于最早到达时刻,且最晚出清发车进路的时间不得晚于最晚出发时间,可表示为

(4)在到发线上的停车时间不得小于最小停站时间,可表示为

(5)到发线占用唯一性,可表示为

(6)同一到发线连续接车时间间隔约束,可表示为

(7)引入变量τi,r表示开始为列车i办理进路r的时刻。若r为接车进路,则;若r为发车进路,则,可表示为

(8)咽喉区进路占用相容性约束,可表示为

(9)到发线与进路匹配约束,可表示为

(10)进出站方向与列车进路匹配,可表示为


(11)压缩后,同一方向进站的列车接发先后顺序不变,可表示为

(12)压缩后,同一方向出站的列车接发先后顺序不变,可表示为

3 算例分析
以某高速铁路车站F为例,某高速铁路车站站场图如图3所示,设有12条到发线,记为l1,l2,…,l12;进路67条,记为r1,r2,…,r67;对应A,B,C,D,E共5个进出站方向。在2 h繁忙时段内,该站到发列车共计60列,将图定到发时刻换算为以s为单位的整数。其中设置为30 s,Tmin设置为180 s。通过咽喉区段的长度和列车的运行速度,可计算出进路的占用时间以及任意2条进路间的冲突度的大小。为了更加直观地对比分析,先将车站2 h繁忙时段内到达的60列车的原到发线运用方案用甘特图形式展示,得到原列车到发线运用方案如图4所示,以时间为横轴,到发线编号为纵轴,矩形的长度表示列车占用到发线的时间,矩形右边数字表示列车编号,以所有列车的最晚的列车出清到发线的时刻作为方案下的列车总运营时间,为7 693 s。
设计2种到发线运用方案,分别为图定到发线运用方案和优化到发线运用方案,并求解模型。图定到发线运用方案与优化到发线运用方案下的到发线运用如图5所示,图定到发线运用方案与原列车到发线运用方案的到发线运用是一致的,图5中深色矩形表示图定到发线运用方案和优化到发线运用方案中到发线运用发生变化的列车,图中上下2部分分别对应图定到发线运用方案与优化到发线运用方案。

图3 某高速铁路车站站场图Fig.3 Station yard map of a high speed railway station

图4 原列车到发线运用方案Fig.4 Original arrival–departure track plan

图5 图定到发线运用方案与优化到发线运用方案下的到发线运用Fig.5 Arrival–departure track utilization in original and optimized schemes
从目标函数值来看,原运行图在图定到发线运用方案下,完成所有列车运行任务的总运营时间由7 693 s减少到了6 882 s,减少的811 s是在不改变到发线运用的基础上,压缩原到发线运用方案的缓冲时间所产生的。在优化到发线运用方案下,总运营时间进一步压缩到6 567 s,较图定到发线运用方案减少315 s,说明改变到发线运用方案起到更好地利用分段解锁疏解列车冲突度,减少总运营时间的作用,即列车间到达间隔得到压缩。模型求解结果如表4所示,优化到发线运用方案比图定到发线运用方案的目标函数少315 s,即总运营时间少315 s,到达间隔得到了4.6%的压缩,为列车完成运营任务预留了更长的缓冲时间。

表4 求解结果 sTab.4 Solution results
对比分析2种方案在到发线组合优化、进路冲突疏解和间隔时间压缩3方面的压缩效果如下。
(1)到发线组合优化。按照车站进出站方向,考虑优化到发线运用方案中到发线发生改变的18列车,同方向前后列车划分为1组,分别计算2个方案中到发线运用对应关联道岔数[9],得到图定到发线运用方案与优化到发线运用方案中关联道岔数如表5所示。优化到发线运用方案中到发线组合对应关联道岔数量较图定到发线运用方案明显减少,根据“到发线组合方案对应关联道岔越少,列车到达间隔时间越短”的到达间隔时间最小的到发线运用规则,优化到发线运用方案更优。

表5 图定到发线运用与优化到发线运用方案中关联道岔数 个Tab.5 Number of associated turnouts in original and optimized schemes
(2)进路冲突疏解。考虑优化到发线运用方案中到发线发生改变的列车,相同进站方向列车划分为1组,计算接车进路与接车进路(以下简称“接-接”)、接车进路与发车进路(以下简称“接-发”)、发车进路与接车进路(以下简称“发-接”)和发车进路与发车进路(以下简称“发-发”) 4种不同类型的冲突度,得到图定到发线运用方案与优化到发线运用方案进路冲突疏解效果如表6所示。由表6可知,优化到发线运用方案相比图定到发线运用方案平均疏解冲突度85 s,5对列车的进路冲突度都得到不同程度疏解,可以得出通过到发线运用优化能够疏解冲突,进而压缩列车到达间隔时间。
(3)列车间隔时间压缩。可分为到达/出发时间间隔压缩和车站间隔时间压缩2种。从到达/出发时间间隔压缩来看,按照车站的衔接方向计算到达时间间隔与出发时间间隔平均值,得到图定到发线运用方案与优化到发线运用方案到达/出发时间间隔如表7所示。经统计,优化到发线运用方案的到达时间间隔平均值相比图定到发线运用方案压缩22 s,出发时间间隔平均值压缩150 s,除B方向到达时间间隔外,优化到发线运用方案的到达/出发时间间隔平均值均小于图定到发线运用方案,故优化到发线运用方案能够实现更大的间隔时间压缩。
从车站间隔时间压缩来看,分别在4种车站间隔时间类型[10]中挑选4组实例,28车与31车间为同方向列车不同时到发间隔时间,11车与27车间为同方向列车不同时发到间隔时间,42车与44车间为敌对进路相对方向列车不同时到发间隔时间,18车与58车间为敌对进路相对方向列车不同时发到间隔时间,对比分析2方案的车站间隔时间压缩效果,得到图定到发线运用方案与优化到发线运用方案车站间隔时间压缩如表8所示。由表8可知,优化到发线运用方案中,4种类型的车站间隔时间较图定到发线运用方案均有较大程度的压缩,其中11车与27车的发到间隔时间压缩了865 s,效果最佳。

表6 图定到发线运用方案与优化到发线运用方案进路冲突疏解效果 sTab.6 Untwining effect of route conflict in original and optimized schemes

表7 图定到发线运用方案与优化到发线运用方案到达/出发时间间隔 sTab.7 Arrival/departure interval in original and optimized schemes
4 结束语
在繁忙时段的高速铁路车站,通过优化列车的到发线运用方案,能够有效压缩车站所有列车运行任务的最小总运营时间,等价于增加到发线运用方案的总缓冲时间。算例分析表明所构建的模型可行,对比方案中前后列车到发线方案组合、进路冲突疏解等,列车到达间隔时间同时能够得到压缩,对于提高高速铁路车站通过能力具有重要意义。未来可在此基础上,对如何提高算例求解速度,扩大研究规模,以及能否以总运营时间最大为目标达到增加更多缓冲时间的目的,做进一步深化研究。

