车轮滚动接触疲劳裂纹萌生寿命预测

于荣泉，李 强，李 娜，郑 静

1.北京交通大学 轨道车辆结构可靠性与运用检测技术教育部工程研究中心，北京 100044；2.南车青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266111)

随着铁路高速重载技术的快速发展，轮轨滚动接触疲劳现象越来越严重，这不但会造成运营和维修成本的大幅增加，同时也直接影响列车运行安全。轮轨滚动接触疲劳现象主要表现为接触表面剥离、压溃和龟裂等，这些疲劳现象与很多因素有关，如轮轨之间的作用力、摩擦因数、表面粗糙度、车辆轨道结构形式及轮轨材料、加工缺陷等[1,2]。众多学者采用不同方法来尽量减缓或阻止轮轨滚动接触疲劳现象的发生，如进行踏面优化以减小轮轨接触应力，发展新型轮轨材料以改善车辆和轨道结构性能，降低轮轨之间的动力作用[3,4]。轮轨滚动接触疲劳现象众多，多数疲劳现象的根源是滚动接触疲劳裂纹的萌生和扩展，因此能够对滚动接触疲劳裂纹萌生寿命与启裂位置做出科学合理的预测，对车辆定期维护具有重要的指导意义。

目前，国内外学者对轮轨滚动接触的研究多基于轮轨材料均匀无缺陷的假设，但车轮在制造过程中会产生多种初始缺陷形式，例如非金属夹杂物、初始裂纹和车轮加工过程中产生的体内残余缩孔、随机气孔及材料空洞等。这些初始缺陷会造成缺陷处应力高度集中，超过材料的屈服极限，发生塑性流动以致断裂，对轮轨滚动接触疲劳影响很大，是车轮产生损伤的主要原因之一[5]。为了研究车轮材料缺陷对滚动接触疲劳的影响，本文利用有限元软件Abaqus建立带材料缺陷的轮轨滚动接触二维有限元模型，模型中将车轮材料缺陷简化为圆形孔。车轮材料循环塑性本构关系采用Lemaitre-Chaboche非线性各向同性/随动硬化模型。研究循环载荷大小、缺陷孔深度及摩擦因数等因素对车轮缺陷孔处损伤参量分布规律及疲劳裂纹萌生寿命的影响。

1 计算模型

1.1 二维赫兹接触理论

假设轮轨接触满足Hertz接触理论的适用条件，则轮轨法向接触压力为二维赫兹分布[6]

( 1 )

式中：p0为接触斑最大接触压力；a为接触斑半轴长度。

最大接触压力为

( 2 )

式中：Pz为接触斑单位长度上的法向接触力，单位为MN/m。

接触斑半轴长为

( 3 )

式中：R1和R2分别为车轮和钢轨的曲率半径；E1和E2分别为车轮和钢轨的弹性模量；ν1和ν2分别为车轮和钢轨的泊松比。本文取E1=E2=210GPa，ν1=ν2=0.3，R1=400mm。

假设轮轨滚动接触处于全滑动状态，接触斑切向力的计算表达式可以简化为

( 4 )

式中：μ为轮轨之间摩擦因数。

1.2 损伤参量与疲劳裂纹萌生寿命模型

1.2.1 损伤参量

临界平面法是以疲劳试验过程中在交变载荷作用下对疲劳裂纹萌生和扩展规律进行观察研究为基础的，具有一定的物理意义。本文采用基于应变能的Jiang-Sehitoglu损伤参量[7]，其表达式为

( 5 )

式中：σmax为裂纹面最大法向应力；Δε为裂纹面法向应变变程；Δτ为裂纹面上剪应力变程；Δγ为裂纹面上剪应变变程；<σmax>=max(σmax，0)；j为材料常数，可由拉扭试验得到，文中材料常数j取0.2[7]。

1.2.2 疲劳裂纹萌生寿命模型

把损伤参量最大值FPmax所在平面定义为疲劳裂纹萌生和扩展的初始平面。这种方法把疲劳裂纹萌生和扩展的物理量通过能量的方式结合起来且综合考虑了裂纹萌生和扩展关键面上应力和应变分量对疲劳裂纹萌生寿命的影响，预测结果与试验有很好的一致性[8]。基于临界平面法的疲劳裂纹萌生寿命模型为

( 6 )

表1 车轮钢寿命预测模型材料参数表[9]

2 有限元模型

2.1 有限元网格及边界条件

利用有限元软件Abaqus建立带缺陷孔的车轮滚动接触二维有限元模型，如图1所示。对于轮轨滚动接触问题，接触区几何尺寸远小于整体特征几何尺寸和接触区域附近的曲率半径，所以轮轨滚动接触幅可看作半无限平面，同时可将轮轨滚动接触问题假设为平面应变问题。有限元模型如图1所示，模型长为200 mm，高为80 mm，接触区长为160 mm，模型中材料缺陷简化为圆形孔，缺陷孔位于接触表面下15 mm处，半径为0.5 mm。缺陷孔附近为高应力应变区，为了保证模型仿真精度并提高计算效率，划分网格时进行了局部细化处理，最小单元尺寸为25 μm，接触表面单元尺寸为1 mm，采用八节点二次平面应变缩减积分单元进行计算。模型中a、b和c三边采用固定全约束边界条件。

图1 含缺陷孔的车轮二维有限元模型

接触载荷反复滚动过程通过在接触表面AB区间内施加移动法向Hertz分布压力和切向分布力来模拟。在起始端A点，移动载荷分多个增量步逐渐加载，通过多个增量步沿x方向逐步移动到终止端B点，通过多个增量步逐渐减至零，这样就完成一次载荷循环过程。反复以上过程可模拟循环滚动过程。

2.2 循环本构模型

材料本构模型采用Lemaitre-Chaboche非线性各向同性随动硬化循环塑性模型[10]，该模型能够合理描述滚动接触条件下材料循环塑性的应力松弛和棘轮效应。材料采用铁路工业常用的BS11普通车轮钢，车轮钢材料参数见表2。

表2 车轮钢循环塑性模型参数表[10]

本构模型的有限元实现应首先确定每个高斯积分点处的应力积分算法。目前应力积分算法主要有两种：显示积分算法和隐式积分算法。隐式积分算法能够满足精度高的要求且当采用与算法一致的切线刚度矩阵时，有限元整体的平衡迭代过程收敛速度明显加快，同时还能保证数值稳定性[11]。目前多数关于弹塑性材料模型的积分计算均采用这种方法，本文亦采用隐式积分算法。

2.3 模型计算参数

分析循环载荷大小、缺陷孔深度和摩擦因数对缺陷孔处损伤参量和疲劳裂纹萌生寿命的影响，单位长度法向接触载荷取8 MN/m、13 MN/m和18 MN/m，缺陷孔距接触表面深度均匀选取5 mm、10 mm、15 mm、20 mm和25 mm等5个深度值，摩擦因数选取0.2、0.4和0.6分别进行计算。

3 结果和分析

通过有限元仿真，获得轮轨循环滚动接触条件下车轮材料的应力应变响应、车轮材料缺陷孔处损伤参量分布特征及疲劳裂纹萌生寿命规律，文中对每一种工况均循环滚动10次。

3.1 应力应变曲线

图2和图3分别表示循环载荷13 MN/m作用下，距接触表面深度为15 mm、半径为0.5 mm的缺陷孔处应力应变分量随载荷循环次数的变化情况。从图中可以看出，经历第一次载荷循环后，缺陷孔处产生y向残余拉应力和y向残余压应变且随着循环载荷次数的增加，残余应力应变分量渐增性收敛且很快趋于稳定。

图2 应力分量随载荷循环次数的变化

图3 应变分量随载荷循环次数的变化

图4给出了循环载荷13 MN/m作用下，深度为15 mm、半径为0.5 mm的缺陷孔处y向应力-应变循环曲线，载荷循环次数为10次。图4可以看出，经过3次载荷循环作用后，随着循环载荷作用次数的增加，缺陷孔处材料y向应力-应变曲线形成稳定的闭环，无塑性应变累积，缺陷孔处材料进入塑性安定状态。

图4 循环载荷作用下应力-应变曲线

3.2 循环载荷

图5所示为循环载荷13 MN/m作用下，深度为15 mm、半径为0.5 mm的缺陷孔处损伤参量最大值随载荷循环次数的变化情况。从图5可以看出，经过三次循环载荷作用后，FPmax值逐渐趋于稳定。当车轮材料应力应变响应趋于稳定时，预测车轮缺陷孔处疲劳裂纹萌生寿命较为合理，结合图3和图4应力应变随循环载荷作用次数的变化情况，可以得到采用10次循环载荷作用后的应力应变数据进行疲劳裂纹萌生寿命预测，结果会更加精确。

图5 损伤参量最大值随载荷循环次数的变化

循环载荷大小分别为8 MN/m、13 MN/m和18 MN/m时，滚过10次后，车轮缺陷孔处沿圆周的损伤参量FP的分布情况如图6所示，图6给出了缺陷孔中心任意平面角度示意图。缺陷孔深度为15 mm，半径为0.5 mm，沿缺陷孔圆周均匀选取50个材料单元，转换模型局部坐标系，计算不同平面角度的损伤参量FP。从图6可以看出，循环载荷大小对缺陷孔处损伤参量FP影响较大，损伤参量FP随着循环载荷值的增加而增大。8 MN/m、13 MN/m和18 MN/m三种循环载荷作用下，损伤参量最大值FPmax分别为1.12 MPa、1.91 MPa和2.72 MPa，所在平面角度分别为194°、173°和144°，可以得到损伤参量FPmax及所在平面角度取决于循环载荷的大小。

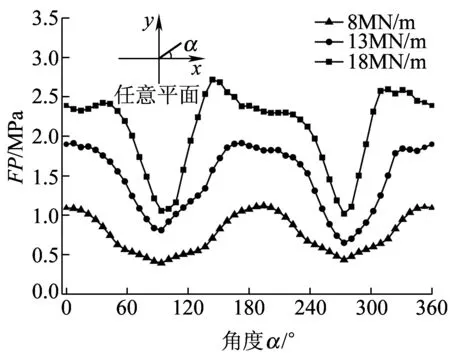
图6 损伤参量随任意平面角度的变化

图7给出了8 MN/m、13 MN/m和18 MN/m三种不同循环载荷作用下深度为15 mm、半径为0.5 mm的缺陷孔处疲劳裂纹萌生寿命随循环载荷值的变化曲线。从图7可以看出，缺陷孔处疲劳裂纹萌生寿命随着循环载荷值的增大而不断减小。在循环载荷13 MN/m作用下，缺陷孔处疲劳裂纹萌生寿命为794次循环。

图7 裂纹萌生寿命随载荷的变化

3.3 缺陷孔深度

图8给出了循环载荷13 MN/m作用下，半径为0.5 mm的缺陷孔处损伤参量随缺陷孔深度的分布曲线。图中选取缺陷孔距离接触表面5 mm、15 mm和25 mm三种工况。从图8可以看出，随着深度的增加，缺陷孔处损伤参量沿圆周的分布曲线逐渐平缓，在25 mm工况下损伤参量分布曲线近似一条直线，在5 mm工况下，损伤参量随角度增加波动比较剧烈，损伤参量FPmax随深度的增加呈不断减小趋势，但损伤参量最小值并没有随着深度的增加而单调减小，在深度为5 mm工况下损伤参量取得最小值。

图8 损伤参量随任意平面角度的变化

图9给出了循环载荷13 MN/m作用下，半径为0.5 mm的缺陷孔处疲劳裂纹萌生寿命随缺陷孔深度的变化情况。如图9所示，两者之间并非线性关系，在5 mm深度条件下，疲劳裂纹萌生寿命为129次循环，而在25 mm深度条件下，疲劳裂纹萌生寿命达到81283次循环。在5～25mm深度范围内缺陷孔深度越深，疲劳裂纹萌生寿命越长；缺陷孔深度越浅，疲劳裂纹萌生寿命越短。

图9 裂纹萌生寿命随深度的变化

3.4 摩擦因数

图10所示为循环载荷13 MN/m作用下，深度为15 mm、半径为0.5 mm的缺陷孔处损伤参量随摩擦因数的变化情况。本文选取了摩擦因数为0.2、0.4和0.6三种情况进行计算。由图10可以看出，三种情况下，损伤参量随角度的变化趋势大体一致。图11所示为循环载荷13 MN/m作用下，深度为15 mm、半径为0.5 mm的缺陷孔处疲劳裂纹萌生寿命随摩擦因数的变化曲线。从图11可以看出，随着摩擦因数的增大，缺陷孔处疲劳裂纹萌生寿命有所降低。纯滚动情况下，缺陷孔处疲劳裂纹萌生寿命为831次循环。摩擦因数为0.6情况下，缺陷孔处疲劳裂纹萌生寿命为588次循环。从结果可以得到，摩擦因数对疲劳裂纹萌生寿命有一定影响，但相比于图7和图9，影响并不明显。

图10 损伤参量随任意平面角度的变化

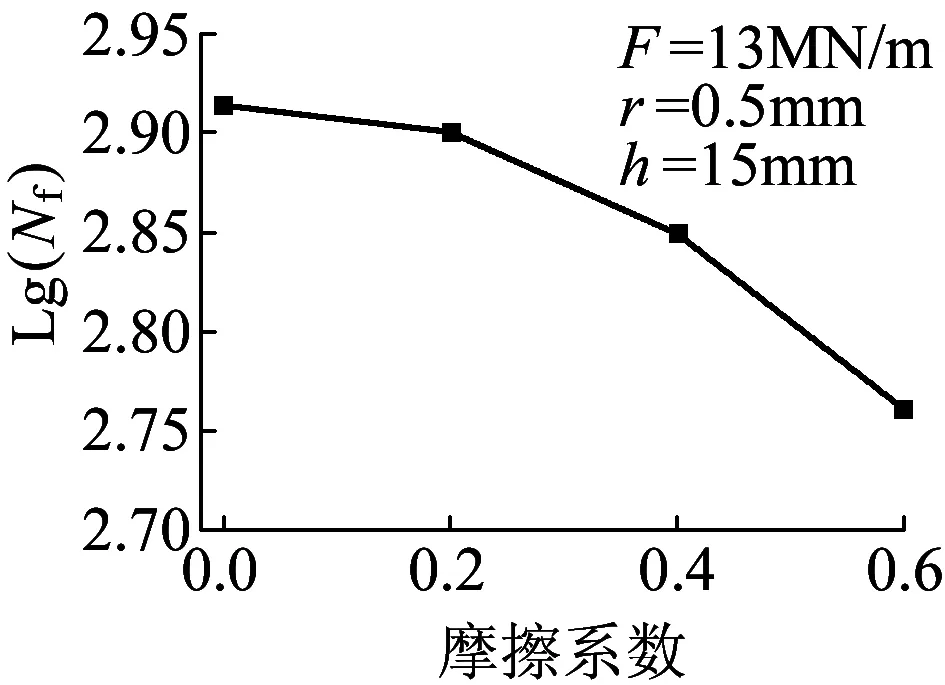
图11 裂纹萌生寿命随摩擦因数变化趋势

4 结论

通过有限元软件Abaqus建立带缺陷孔的车轮二维有限元模型，材料循环本构关系选用Lemaitre-Chaboche非线性各向同性/随动硬化模型，分析缺陷孔处应力应变特性，运用基于临界平面法的疲劳裂纹萌生寿命模型进行车轮缺陷孔处疲劳裂纹萌生寿命预测。得到如下结论：

(1) 经历首次载荷循环后，缺陷孔处产生y向残余拉应力和y向残余压应变，且随着循环载荷次数的增加，残余应力应变分量呈渐增性收敛且很快趋于稳定。

(2) 利用Jiang-Sehitoglu损伤参量得到不同循环载荷、不同深度和不同摩擦因数作用下车轮缺陷孔处沿圆周的损伤参量分布规律。

(3) 缺陷孔处疲劳裂纹萌生寿命随着循环载荷和摩擦因数的增大而呈单调递减趋势，但随缺陷孔深度的增加而增大。相比于循环载荷和缺陷孔深度，摩擦因数对缺陷孔处疲劳裂纹萌生寿命影响较小。

参考文献：

[1]金学松，沈志云.轮轨滚动接触疲劳问题研究的最新进展[J]. 铁道学报, 2001,23(2)：92-107.

JIN Xue-song, SHEN Zhi-yun. Rolling Contact Fatigue of Wheel/Rail and its Advanced Research Progress[J]. Journal of the China Railway Society，2001,23(2)：92-107.

[2] 温泽峰，金学松. 非稳态纯滚动接触弹塑性分析[J]. 固体力学学报,2006, 27(4):355-361.

WEN Ze-feng ,JIN Xue-song.Elastic-plastic Analysis of Non-steady State Pure Rolling Contact[J].Acta Mechanica Solida Sinica, 2006,27(4):355-361.

[3]邓铁松，李伟，温泽峰，等.钢轨滚动接触疲劳裂纹萌生寿命预测[J]. 润滑与密封,2013,38(8)：46-51.

DENG Tie-song,LI Wei, WEN Ze-feng, et al. Prediction on Rolling Contact Fatigue Crack Initiation Life of Rails[J].Lubrication Engineer, 2013,38(8)：46-51.

[4] 常崇义. 有限元轮轨滚动接触理论及其应用研究[D]. 北京：中国铁道科学研究院，2010.

[5] 张斌，卢观健，付秀琴,等.铁路车轮、轮箍失效分析及损伤图谱[M].北京：中国铁道出版社, 2002.

[6]JOHNSON K L. Contact Mechanics. Cambridge University Press[J], Cambridge, 1985.

[7] SEHITOGLU H, JIANG Y. A Model for Rolling Contact Failure[J]. Wear, 1999,224(1):38-49.

[8]王建西，许玉德，练松良，等. 随机轮轨力作用下钢轨滚动接触疲劳裂纹萌生寿命预测仿真[J]. 铁道学报,2010,32(3):66-70.

WANG Jian-xi, XU Yu-de, LIAN Song-liang, et al. Simulation of Predicting RCF Crack Initiation Life of Rails under Random Wheel-rail Forces[J]. Journal of the China Railway Society,2010,32(3):66-70.

[9] EKBERG A. Life Prediction of Rolling Contact Fatigue Crack Initiation[J]. Int J Fatigue, 2001,23(7):575-583.

[10] EKH M, JOHANSSON A, THORBERNTSSON H, et al. Models for Cyclic Ratchetting Plasticity-integration and Calibration[J]. Trans ASME J Eng Mater Technol, 2000,122:49-55.

[11] 康国政，高庆. 棘轮行为及其本构模型和工程应用的研究进展[J]. 应用力学学报，2008，25(3)：455-461.

KANG Guo-zheng, GAO Qing. Advances of Ratcheting in Cyclic Constitutive Models Applications[J]. Chinese Journal of Applied Mechanics, 2008，25(3)：455-461.