地铁乘务排班计划优化的最短路快速算法

薛锋，梁鹏，李海，陈崇双，周天星

(1. 西南交通大学 交通运输与物流学院，四川 成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3. 综合交通大数据应用技术国家工程实验室，四川 成都 611756；4. 西南交通大学 数学学院，四川 成都 611756；5. 中铁二院工程集团有限责任公司 交通与城市规划研究院，四川 成都 610031)

乘务计划是地铁运营组织计划中的核心工作之一，一般分为排班计划和轮班计划；其中排班计划是寻找列车车次与乘务任务之间的对应关系，是轮班计划的基础，也是整个乘务计划编制过程中较为复杂的工作。乘务排班计划是交通运输领域研究的热点问题之一，目前对于乘务计划编制问题的研究主要集中于铁路、航空及城市公交方面。其中铁路方面的研究可以为城市轨道交通乘务排班提供很好的参考。HANAFI 等[1]构建了最小化乘务组费用的优化模型以得到最优乘务交路方案；LUCIC 等[2]将乘务排班计划分为2 个阶段，设计了基于启发式算法与模拟退火技术的2种求解方法；FRELING等[3]利用价格分支算法对乘务排班计划问题进行建模和求解；杨国元等[4]设计了基于遗传算法的模型求解算法对铁路客运乘务排班计划进行编制；符卓等[5]建立了编制日乘务交路的0-1整数规划模型，并给出了基于禁忌搜索算法的求解方法；林枫[6]将乘务交路计划编制过程分为两阶段，并设计了MOMS求解算法；杨嘉宝等[7]建立了乘务交路回路优化模型，给出了蚁群-遗传混合求解算法。在城市轨道交通方面，CHU[8]从多个阶段对乘务排班计划进行研究，并分别采用了最短路算法、对称匹配和改进遗传算法进行求解；JANACEK 等[9]将根据时间段分成的多个区间作为列生成算法中的一个子问题进行并行求解；张增勇等[10]利用改进的Dijkstra 算法和离散粒子群算法给出了乘务作业段生成模型和乘务工作班生成模型的求解方法；石俊刚等[11]建立了城轨乘务任务配对模型，并基于列生成思想对其进行求解；许仲豪等[12]研究了基于列生成算法的乘务排班计划优化模型；丰富等[13]基于时间均衡度构建了乘务排班计划模型，并提出了基于遗传算法的求解方法；金华等[14]研究建立了乘务排班计划集合覆盖模型，通过将定价子问题转化为网络图集合的最短路问题设计了列生成法求解算法。本文基于最短路算法思想，提出一种乘务排班计划优化编制方法：在考虑便乘的情况下，建立了乘务排班计划接续时间最少和总运营成本最小为目标的优化模型；以乘务作业段为顶点、乘务作业段之间的接续关系为弧，将乘务排班计划转化成求解网络图中的最短路问题，提出了一种基于SPFA 的求解算法。该方法计算简便、快速，能实际应用于城市轨道交通尤其是地铁乘务排班计划问题的求解。

1 问题的描述与分析

地铁乘务排班计划编制是将地铁线路的乘务段经过计算与编排，得到乘务排班日计划的过程。其编制步骤为：

1) 根据地铁的运行区段及其到发点确定乘务片段；

2) 根据乘务片段构建乘务作业段；

3) 根据乘务作业段编制乘务任务。

轮乘站是地铁线路上特殊的车站，是乘务员交接班、用餐的固定地点，因此可以作为划分乘务作业段的依据。乘务作业段是乘务员值乘的基本单元，代表着相邻2个轮乘站之间的一段驾驶任务。乘务任务是一名乘务员当班值乘的乘务作业段的组合，乘务排班日计划即为所有乘务任务的组合。

以图1 为例，“110”等为车底编号，该线路上的轮乘站将此线路划分为一个个乘务作业段，而各个乘务作业段由一个或多个乘务片段组成，满足接续时间要求(即，休息时间满足约束)的乘务作业段即可组合形成乘务任务，多个乘务任务即可组成乘务排班日计划。

2 数学模型的建立

以轮乘站为分割点将以列车运行线为依据的乘务活动分割成一系列的乘务作业段，以日为时间周期，将一天之内的乘务作业段按照时间分为早班、白班、夜班3个时间段的乘务作业段，以此构建乘务作业段的接续时间矩阵，如表2所示。

表2 乘务作业段接续时间矩阵Table 2 Connecting time matrix of crew work-pieces

表2 中，行与列均表示不同组的乘务作业段。其中Pi(i=1，…，a)为早班时间段的乘务作业段(共有a个)；Qi(i=a+1，…，a+b)为白班时间段的乘务作业段(共有b个)；Ri(i=a+b+1，…，a+b+c)为夜班时间段的乘务作业段(共有c个)。令n=a+b+c为乘务作业段的总数，Cij(i，j=1，…，n)为乘务作业段Pi(或Qi，Ri)与乘务作业段Pj(或Qj，Rj)之间的接续时间。

由于乘务作业段根据作业时间被分为了早、白、夜3个班次，乘务作业段只能按照时间顺序向后接续，同一班次或不同班次的乘务作业段不能逆时接续；同时约定不同班次的乘务作业段之间不能接续，其接续时间用一个足够大的正整数M表示。同时，若乘务作业段间的接续时间不满足休息时间约束，则这样的乘务作业段无法相互接续，其接续时间也用M表示。

2.1 最小化乘务排班计划总接续时间优化模型

按照上述思路，可建立以乘务排班计划总接续时间最小为优化目标的模型，如式(1)所示。其中Z为乘务排班计划总接续时间，Cij为乘务作业段之间的接续时间；xij为0-1 变量，当其为1 时，表示乘务作业段i接续乘务作业段j；当其为0 时，表示乘务作业段i不接续乘务作业段j。

同时对乘务作业段的接续进行约束，使得2个乘务作业段之间最多只能接续一次。式(2)表示每个乘务作业段在排班计划中有且仅有一个紧前作业段；式(3)表示每个乘务作业段在排班计划中有且仅有一个后续作业段，也就是乘务作业段i和j最多配对接续一次，求和均为0时表示该乘务作业段未能与其他乘务作业段接续，成为单个乘务作业段的乘务任务。

对乘务作业段之间的接续时间进行约束，使其满足乘务作业段间的休息时间约束，如式(4)所示；对乘务任务中的司机连续工作时长进行约束，使其工作时长不能超过给定的连续工作时长限制，如式(5)所示；对乘务任务中的吃饭时间进行约束，使其满足吃饭时间标准，如式(6)所示。

式中：Cmin为乘务作业段间的最短休息时间；Cmax为乘务作业段间的最长休息时间；tj为乘务作业段j的司机工作时间；t0为乘务任务的第一个乘务作业段的工作时间；T为司机连续工作时间限制；tcf为一个乘务任务中的吃饭时间；tcfmin为最短吃饭时间；tcfmax为最长吃饭时间。

式中：K为便乘时间；ebc为便乘时间的惩罚因子，其取值视便乘的实际成本而定，tbc为乘务作业段i与乘务作业段j之间的便乘时间，aij为0-1 变量，当其为1时，表示乘务作业段i与乘务作业段j之间存在便乘，当其为0时则不存在便乘。

将2个优化目标结合，形成一个总时间最少的优化模型。

2.2 最小化乘务排班计划总运营成本优化模型

由于各乘务作业段的起止时间都已确定，且乘务员的总在车时间也为固定值，则乘务排班计划的运营成本都体现在乘务员的工资上。所以，要减少乘务排班计划所需的费用，就需要尽量减少乘务任务的数量，即增加每个乘务任务包含的乘务作业段的数量，使得乘务作业段之间的接续数量最大，如式(9)所示。

由此构成了一个最小化乘务排班计划总时间和总费用的双目标优化模型，此模型以式(9)为主要优化目标，式(8)为次要优化目标，更具有通用性。

3 求解算法

本文采用最短路方法进行求解，分早、白、夜班3个部分分别构成网络图。将乘务作业段作为网络图的顶点，乘务作业段的接续关系作为弧，与xij相乘的数作为网络图中弧上的权值，即ωij=Cij+ebctbcaij，一条网路图中的最短路径即为一个乘务任务，因此乘务排班日计划即为网络图中多个最短路径的集合。图2为乘务作业段形成的网络图(中间的时间点已省略)。对于乘务排班网络，采用SPFA 算法[15]进行最短路径的求解。SPFA 算法是求解单源最短路径问题的一种算法，采用了动态优化逼近的思想。算法的基本步骤如下。

Step 1：以轮乘站为起止点，将乘务片段集合组合成乘务作业段的集合Pi(或Qi，Ri)。

Step 2：以乘务作业段为顶点，乘务作业段之间的接续关系为边，ωij=Cij+ebctbcaij作为边上的权值，构成早班、白班及夜班的3个网络图。

Step 3：初始化一个D数组，由顶点和顶点对应的权值构成，数组中的顶点为Pi，除了起点P1赋值为0外，其他顶点对应的权值都赋予无穷大，这样有利于后续的松弛。同时把起点P1加入循环队列，从此处开始进入循环，直到队列为空才退出循环。

Step 4：首先进行第一次循环，循环队列的第一个顶点P1出列，然后对以P1为弧尾的边对应的弧头顶点进行松弛操作，若P1到该顶点的最短路径变短了，则更新循环数组中该顶点的权值为新的最短路径。当顶点都被松弛了，而且不在队列中时，就把它们加入循环队列中。

Step 5：进行第2 次循环，新的队首元素出列，然后对以队首元素为弧尾的边对应的弧头顶点进行松弛操作，步骤与Step 4类似，数组的权值及循环队列中的顶点再次更新。

Step 6：按照上述方法对队列进行更新，一直到队列为空才退出循环，此时数组里就保存了从源点到各顶点的最短路径值，以此得到起点P1到各个顶点的最短路径的值。

Step 7：先在其中选取满足式(9)的路径，此时被选择的路径为运营成本最小的路径，在此基础上，再从被选择的路径中选取满足式(8)的路径，作为最终求得的以P1为起点的最短路径。

Step 8：更换起点为Pi，将以P1为起点的最短路径经过的点去除，从Step 4重新开始循环，一直到退出循环，再求得以Pi为起点的最短路径。

Step 9：遍历早班时间段的a个顶点，直到所有顶点均被求得的路径包含其中，由此求得的各个最短路径即为早班时间段的乘务任务。

Step 10：将白班时间段与夜班时间段的各个乘务作业段按照上述方法进行求解，由此求得的所有最短路径即为一天的乘务排班计划。

4 实例分析

本文以成都地铁5 号线为例编制乘务排班计划。采用C++编程实现上述模型和算法，并在CoreTMi5 2.3 GHz主频、16 G内存的计算机上运行。

成都地铁5 号线共设有41 个车站，其中轮乘站8 个，用S1-S8 来表示，将乘务片段组合成乘务作业段的3个时间段集合，其中早班时间段的乘务作业段有267 个，白班时间段的乘务作业段有201个，夜班时间段的乘务作业段有218个，乘务作业段总数为686个，如表3所示。

表3 乘务作业段集合Table 3 Collection of crew work-pieces

由于各个乘务作业段的起止时间已经确定，在休息时间约束Cmin=10 min，Cmax=30 min 的情况下，接续时间矩阵中Cij的取值便可以确定。不同时间段的乘务作业段不能接续，因此其接续时间均为一个足够大的正整数M，各乘务作业段之间的接续时间便可以确定，如表4所示。以乘务作业段为顶点，乘务作业段之间的接续关系为边，结合便乘情况确定各边的权值，构成成都地铁5号线早班、白班及夜班的3个网络图。随后按照上述算法步骤进行求解，经过若干次循环，求得早班、白班及夜班的乘务排班计划表如表5所示。

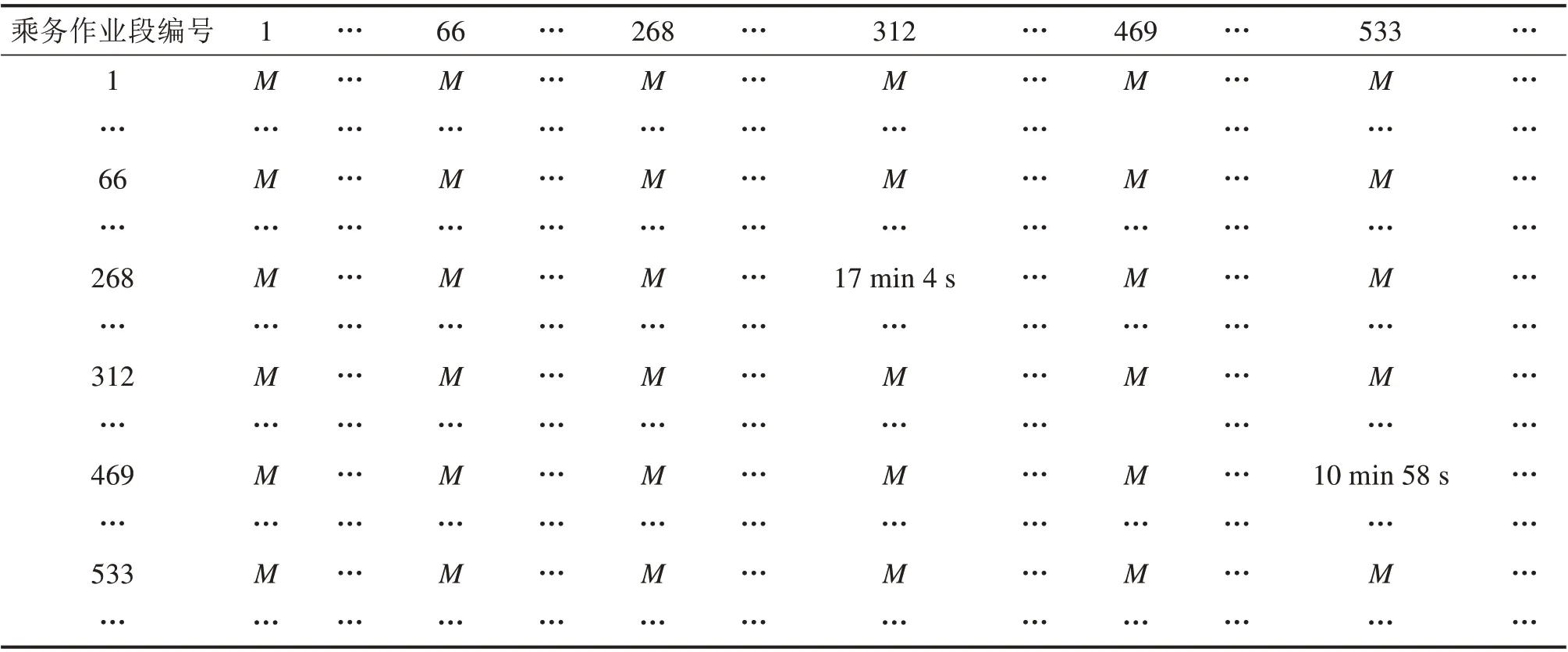
表4 5号线乘务作业段接续时间矩阵Table 4 Connecting time matrix of metro line 5’s crew work-pieces

表5 乘务排班计划Table 5 Crew scheduling

在最终求得的乘务排班计划中，早班有乘务任务53 个，白班有乘务任务41 个，夜班有乘务任务49 个，乘务任务总数为143 个。早班任务时长为280 h 34 min 57 s，白班任务时长为199 h 54 min 51 s，夜班任务时长为215 h 25 min 37 s，总任务时长为695 h 55 min 25 s。早班、白班、夜班的乘务任务时长统计图如图3～5 所示，从中可以看出求得的乘务任务时长较为均衡。

采用本文所给出的模型与算法求得的乘务排班日计划结果与手工方法所求得的结果对比情况如表6和表7所示。

从表6 和表7 可以看出，本文所提出的乘务排班计划算法具有以下优点：

表6 乘务任务数量对比Table 6 Comparison of the number of crew tasks

表7 乘务任务工作时长对比Table 7 Comparison of the duration of crew tasks

1) 在满足相应约束条件的同时，该算法所求得的乘务任务数量较小，使得乘务排班计划的总成本较小。

2) 该算法所求得的各乘务任务的总接续时间较小，使得乘务排班计划的总工作时间较小，效率较高。

3) 该算法减少了便乘情况的发生，使得乘务人员的乘务任务执行效率较高。

上述结果表明，在满足同样的运输需求前提下，本文算法可提高乘务计划的效率，降低乘务员的实际工作量。

5 结论

1) 通过本文所提出的模型算法及实例分析表明：相比于手工编制，本文方法编制的乘务排班计划中，总乘务任务个数减少了大约4.03%，总工作时长减少了大约1.97%，由此可以看出，本文方法可以有效减少乘务排班计划的成本及工作时长。

2) 将乘务作业段按照时间分成了早班、白班、夜班3部分，使得算法求解的时候不需要再遍历所有乘务作业段，只需要进行各个时间段内的乘务作业段的相互配对，显著减少了算法的搜索时间。