基于混合遗传算法的混堆箱区内场桥调度研究

郑红星,于 凯

(大连海事大学交通运输管理学院,辽宁大连116026)

基于混合遗传算法的混堆箱区内场桥调度研究

郑红星*,于 凯

(大连海事大学交通运输管理学院,辽宁大连116026)

所谓混堆模式下集装箱箱区内场桥调度问题,是指在固定时段内,将有限的场桥资源在混堆模式集装箱港口堆场的单个箱区内进行分配和排序,以最大限度地减少该时段内所有任务的等待成本和场桥非装卸成本为目标,并保证不能超过场桥的作业强度极限.在充分考虑了多场桥作业时须有安全距离和不能相互跨越,以及内外集卡的优先级有差异和集卡等待时间有上限等现实约束下,对此问题构建了非线性数学规划模型.基于问题自身的特点设计了基于任务排序的染色体结构,用融入禁忌搜索的混合遗传算法进行求解.最后通过实例分析证明了模型和算法的有效性.

水路运输;系统工程;场桥调度;混合遗传算法;混堆箱区

1 引 言

随着集装箱贸易量的日益增长,以及港口自身堆场面积有限,许多集装箱港口采用混堆模式来进行堆存,该模式下堆场的相关问题是当前港口研究的热点之一.很多国内外学者对混堆模式下港口的堆场进行了研究.Gambardella L.M等提出了混堆模式下集装箱堆存的优化模型[1];王斌研究了滚动周期内进出口随机箱量最佳分配方法[2];郑红星等在滚动式计划的基础上,以新增集装箱压箱数最小为目标构建了箱位指派优化模型,并设计了相应的启发式算法求解[3].

就混堆模式下堆场作业效率和效益而言,箱区内场桥的调度是其中的关键.对于场桥调度问题,很多国内外相关学者都进行了较深入的研究,其中单场桥调度文献有:Kim H.K.等研究了单个场桥对外集卡的交箱和取箱任务的作业序列问题[4];韩晓龙研究了装船过程中单台龙门吊的最优路径问题[5];W.C.Ng等在一个给定了装卸量且各任务就绪时间不同的堆场内研究场桥调度问题[6].多场桥调度的文献有:Wenkai L等考虑了更多的现实约束,建立多场桥调度模型,并使用启发式和水平滚动算法求解[7];Matthew E.H.P等建立了多场桥实时控制系统,利用仿真进行了分析[8];乐美龙,林艳艳等考虑场桥实际作业约束,建立多场桥混合整数规划模型并设计了两阶段启发式算法[9],但只考虑了两台场桥的调度.

综上,针对混堆模式下堆场的研究主要集中在各箱区作业箱量的平衡和不同箱型的箱位指派上,对于该模式下堆场的其他方面研究甚少.而对于堆场单箱区内场桥调度的研究,大都针对分堆模式,且假定该箱区内作业场桥的数量既定,并没有考虑该数量是否合理.

本文针对在混堆模式下的堆场内,假定一段时间内各任务位置及对应集卡到达时刻都已知,考虑内外集卡优先级别的差异,构建了单箱区内场桥调度优化模型,以该时段内所有任务的等待成本、场桥非装卸成本(场桥移动成本和空闲等待成本)最小化为目标,设计了混合遗传算法求解模型,最后用实例验证了算法与模型的有效性.

本文与已有文献的主要不同之处如下:

(1)考虑集卡到达堆场指定作业位置时间的影响,该因素直接影响场桥的调度方案,而以往文献大多未考虑;

(2)研究外集卡在堆场等待时限对场桥调度的影响,在现有文献中,大多欠考虑这方面的因素;

(3)研究内外集卡优先级对混堆模式下场桥调度的影响,在已有文献中基本没有涉及;

(4)研究箱区中场桥的配置与调度集成优化,在现有文献中大多只研究场桥配置既定的调度问题,而不考虑配置是否合理.

2 问题描述

在混堆箱区内某个箱位对应的箱型可能是进口箱、出口箱、进箱、待提箱其中的一个,等待服务的集卡包括内外集卡且它们的作业时间和要求也各不相同,从而导致场桥调度更复杂,如图1所示.因此在某一固定时段内,只有给混堆箱区配备合理台数的作业场桥,并确定这些场桥的合理作业顺序,才能既满足客户的服务水平,又不至于使港方的成本过高.

图1 一个混堆集装箱箱区示意图Fig.1 The schematic diagram of a mixture storage block

本文研究的是混堆模式下集装箱港口的某箱区,在某段时间内各任务贝位和集卡到达时间已知的场桥调度优化问题.为了最大限度地同步优化箱区内场桥配置以及各场桥的作业序列,文中构建了一个以该时段内所有任务的等待成本、场桥非装卸成本最小化为目标,并保证当配有多台场桥时,场桥间须有安全距离且不能跨越的调度模型.

3 场桥调度模型

3.1 模型假设

(1)单个混堆箱区内最多配置3台场桥,至少配置1台场桥.

(2)所有任务位于同一混堆箱区,箱位既定且各任务对应集卡的到达时刻可知.

(3)各场桥的劳动时长均不得超过其劳动强度上限值.

(4)当箱区内配置多台场桥时,桥间不能穿越且有一定的安全作业距离.

(5)外集卡超过等待上限后其优先级高于未超过上限的内集卡,内集卡超过等待上限后服务优先级最高,场桥必须为其服务.

3.2 模型建立

参数描述:m为场桥编号;n为某时段箱区内任务总数;Xim为场桥m第i个装卸的任务编号;Y为某时段箱区内配置的场桥数;Km为场桥m装卸的总任务数;r(Xim)为任务Xim的对应集卡到达作业位置时刻;h(Xim)为场桥m装卸任务Xim需要的时间;t(Xim)为场桥m完成第i次装卸的任务的时刻;Fm为场桥m完成其任务集中最后一个任务的时刻;W(Xim)为0-1变量且当Xim对应集卡是内卡时取0,否则取1;C(Xim)为任务Xim对应的集卡等待单位时间的成本,而且变量具体取值为

d(X(i-1)m,Xim)表示场桥m从任务X(i-1)m移动至任务Xim处所需的时间;B(Xim)为场桥m第i次装卸的任务所处贝位;B(X0m)为计划期初场桥m所处的贝位号;B0为一个箱区内总的贝位数;为t时刻场桥m所处的贝位;为0;bsafe为相邻场桥间留有的安全作业贝位数;t(X0m)用于定义初始的系统当前时刻为0;C为场桥空闲单位时间的成本;C0为场桥大车移动单位时间需要的成本;T1为内集卡的等待时间上限值;T2为外集卡的等待时间上限值;V0为场桥大车移动速度;l0为单个贝位的长度;T为单个计划期时长.上述参量中Xim、Km、Y是模型的决策变量.

目标函数 Minf=α·(f1+f2)+(1-α)·f3

约束条件

以上式中m=1,2,…,Y.

在上述模型中,目标式中的f1为场桥空闲成本,用每台场桥完成其最后任务的时刻,减去该场桥用于装卸和大车移动的时间,然后汇总乘以单位时间空闲成本;f2为场桥移动成本,用每台场桥完成所有任务的大车移动时间乘以单位时间移动成本,然后汇总;f3为所有集卡总的等待成本,用每个集卡的作业完成时间减去该集卡的到达时间和装卸时间,并视集卡不同类型再减去30 min(即当为内集卡时,只要等待就会产生等待费用;当为外集卡时,等待时间超过30 min才会产生等待成本),最后汇总并乘以单位时间的集卡等待成本.对于权重值α,本文将在算法中为两部分设置权重(实际工作中可参考决策者的偏好或港口具体情况而定),并以加权总成本作为目标函数值.

约束(1)保证任一个任务的完成时刻不早于该任务到达时刻与装卸时间之和;约束(2)为某任务完成时刻、集卡到达时刻、装卸时长等之间的等式约束;约束(3)为场桥从某任务行走到下一任务所需时间的等式约束;约束(4)、(5)、(6)共同保证了一个任务只能由一台场桥装卸且只能被装卸一次;约束(7)保证场桥之间不会出现穿越同时保证留有安全作业距离;约束(8)保证在计划时段内任意时刻各场桥均不能跑出箱区;约束(9)为任务等待单位时间的成本取值约束;约束(10)为内外集卡的判断并赋值为1,0;约束(11)保证各任务的等待时间不能超过对应上限;约束(12)保证各场桥的作业时间不超过计划期的80%,即不超过最大劳动强度;约束(13)为各参数取值约束;约束(14)为决策变量的范围约束.

4 模型求解

针对模型的特点,本文设计了混合遗传算法(HGA),把TS的记忆功能引入到GA进化过程之中并用TS算法增强GA的爬山能力,具体算法如下所述.

4.1 染色体编码

采用实数编码,一个调度方案对应的染色体长度为(任务数+场桥数-1),各基因值为任务编号,“0”基因为不同场桥间的间隔符号,例如10任务由3台场桥共同装卸的一个调度方案对应的染色体结构及说明如图2所示.

图2 染色体编码展示Fig.2 The show of chromosome coding

4.2 初始种群的生成

在生成初始种群时,要满足约束(4)、(5)、(6),以保证生成的染色体无重复的基因值.还须满足当有两台作业场桥时保证染色体中“0”不能处于基因链的首尾位,三台作业场桥时保证染色体中有2个“0”基因,且“0”不能处于基因链的首位或出现两个“0”相邻的情况,避免生成的染色体无意义.

4.3 适值函数

算法中个体的适值函数用个体的目标值函数变化而成.为满足约束(7),当个体对应方案出现跨越或干扰时该类个体的适值将被明显区分,如下式:

在算法中计算f(Xi)时引入一惩罚规则来满足约束(11),当个体对应的方案有集卡超过等待上限,给该个体的目标值加上一个M(一较大的正数)值作为惩罚.

4.4 选择操作

考虑到当一个箱区内配备多台场桥作业时,各代种群中有较多个体对应的方案会有干扰或跨越.为了避免选择该类个体,文中采用以下选择流程:

Step 1 在当前种群任意选择一个体,拨一次轮盘产生一随机数.

Step 2 若当前个体满足被选条件且该个体对应方案无干扰或跨越,则选择此个体进入交叉池,否则返回step 1.

Step 3 盘点已选的个体总数,如果达到种群容量就停止选择操作,否则,转回step 1.

4.5 交叉操作

针对染色体编码特点,本文采用顺序交叉,如图3所示,具体步骤如下:

Step 1 随机选择两个交叉点X,Y确定两父体中将被复制到子代的基因片段,并初步得到两个不完整的子代a、b.

Step 2 对两个父个体从第二个交叉点Y后开始列出原基因码顺序,得到两个父个体的基因码排列.

Step 3 从父体1、父体2的基因码排列中分别删掉父体2、父体1已复制到子代的基因码,分别得到排列a'、b'.

Step 4 对a,从第二个交叉点开始按顺序将排列b'的基因码从左往右填入对应的基因位并替换“×”.对b做同样操作,完成后得到两个完整的子个体.

当箱区内场桥的数量是三台时,染色体中有两个“0”出现,此时可能会删除过多的“0”导致个体不一样长.因此本文规定删除排列出的基因码是按照“只删首次重复基因”规则,这样可防止以上错误情况出现.

4.6 禁忌变异操作

考虑模型的特点,本文设计了“禁忌变异(TSM)算子”.

邻域设计:文中邻域构造采用解(染色体)的简单变化实现,即交换染色体中除了“0”之外的任意两个基因位的值.邻居数为C2n,当任务数较大时邻居过多,因此采用选择目标升序排列,并选前20%的邻居作为候选集合.

禁忌表:文中选取的禁忌对象有两类,一类是,导致目标值变大超过30%的解被禁.另一类是,交换基因值后出现场桥穿越或干扰的所有对象被禁.禁忌长度为

特赦规则:当候选集中目标值最好的个体被禁,如果此个体的目标值小于当前最优值,则解禁.

TS的终止原则:当迭代次数达到终止上限Kmax时终止.

禁忌变异算子求解流程如图4所示.

图3 染色体交叉过程Fig.3 The crossover process of chromosomes

图4 禁忌变异流程Fig.4 The process of TSM

4.7 HGA终止规则

对于HGA的终止规则,本文采用当算法的迭代次数达到预设的上限时终止计算.

4.8 HGA的性能分析

为了获知本文设计的HGA是否提高了传统GA的性能,分别用GA和HGA求解某具体问题.针对一箱区内具有较多装卸任务的场桥调度问题进行求解,相关实验数据如表1、表2所示.

对于GA和HGA的染色体编码、生成初始种群、适值计算、个体的选择等均采用上文提出的方式.在实验中,GA及HGA使用的遗传参数为:群体大小300,交叉概率和变异概率分别为0.4和0.08,终止代为1 000.最终GA搜索到900代左右目标值收敛于1 600元.对于HGA仅搜索到650代左右目标值就收敛于1 400元.图5和图6分别给出了使用HGA和GA的搜索过程.

表1 箱区内任务情况Table 1 The task condition in a mixture storage block

表2 模型中相关参数取值Table 2 The parameter values of the model

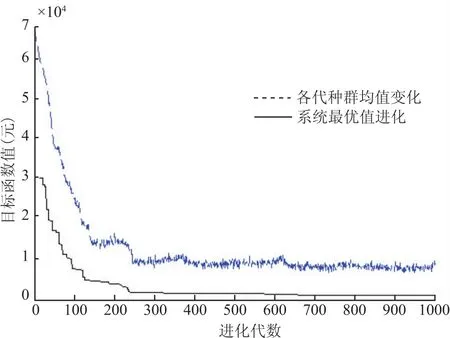
图5 HGA的搜索过程Fig.5 The search process of HGA

图6 GA的搜索过程Fig.6 The search process of GA

从图6可以看出,GA的收敛速度比较缓慢而且群体的均值不稳定,目标值400代左右首次稳定,在第580代开始爬山.而观察图5可知HGA的收敛很迅速且群体的均值较稳定,目标值230代左右首次稳定,很快在第320代就开始爬山,并在650代停止搜索.因此,针对本文提出的调度模型, HGA相比传统GA更有效.

5 实例分析

5.1 实例描述

某集装箱港口内某混堆箱区2个小时内有26个需装卸任务,各任务位置、对应集卡到达时间、装卸时长、对应集卡类型等具体见表3;场桥移动速度、行走和空闲成本率、内外卡等待成本率等参数见表4.

表3 箱区内任务情况Table 3 The task condition in a block

表4 参数取值Table 4 Parameter value

5.2 结果分析与比较

采用MATLAB软件编程实现HGA,实验在Intel Pentium Dual-Core T2080 1.73GHz的处理器, 2GB内存的PC上进行,并设置种群大小Popsize为300,交叉概率Pc为0.4,变异概率为Pm= 0.08,HGA的最大迭代次数为1 000,禁忌变异操作中算法迭代上限Kmax为500.

经多次实验,系统最优值随着遗传代数增加收敛效果如图7所示,在第940代,目标值收敛于1 355.24元.对应的配置作业场桥数为2,调度方案为YC1:2→1→5→9→12→15→23→22→17→19; YC2:6→3→4→7→8→11→14→18→10→16→13→21→20→25→24→26,该方案的相应评价指标值见表5.为了直观看出方案是否出现场桥间跨越或干扰,绘制了两台场桥的实时行走路径,如图8所示,从图中可看出两场桥路径无交点,即求得的优化调度方案确实未出现场桥间的干扰或跨越.

图7 目标值收敛过程Fig.7 Convergence process of objective value

图8 两场桥实时行走路径Fig.8 Real-time paths of two yard cranes

表5 优化调度方案评价表Table 5 The evaluation table of optimized scheme

在集装箱堆场实际工作中,通常采用的场桥调度规则为先到先服务(FCFS)和就近原则(Adjacent).针对文中案例,采用上述两个规则得出的调度方案与方案的各项评价指标值如表6和表7所示.

表6 传统调度规则下的场桥调度方案Table 6 The YC scheduling based on common rules

表7 FCFS与Adjacent的调度方案评价表Table 7 The evaluation table of scheme(FCFS&Adjacent)

对比表5和表7,可以看出三个方案中:采用文中模型得出调度方案的目标总成本(对应表中的加权成本)和场桥总空闲成本最低,同时完成所有集卡装卸任务的总时间最短,并且所有的集卡完成时限都未超等待上限(内卡10分钟,外卡30分钟).从以上对比分析可知,同采用传统调度规则相比,文中模型求得的调度方案更合理.

6 研究结论

混堆模式下集装箱堆场的作业量和频次非常大,如何有效地利用有限数量的场桥以保证堆场的工作效率和效益具有重要的现实意义.本文针对混堆模式下港口的单箱区某时段内的场桥调度问题,重点考虑内外集卡的优先级、场桥间不可跨越和需有安全距离,以及集卡等待时间的上限4个方面,建立了场桥调度优化模型,设计了混合遗传算法进行求解.算例结果表明,本文提出的场桥调度模型能确定箱区配置作业场桥的合理数量及其作业序列,并在保证堆场作业效率的同时降低生产运营成本,可为混堆模式下场桥的实时调度提供决策支持.

本文研究中将各任务需要的装卸时间视为已知,但实际作业中由于倒箱的影响,会使得某些任务的装卸时长有所偏差.因此在本文研究基础上,可将倒箱问题加入研究中.

[1] Gambardella L M,Mastrolilli M,Rizzoli A E,et al.An optimizationmethodologyforintermodalterminal management[J].Journal of Intelligent Manufacturing, 2001,12(5/6):521-534.

[2] 王斌.集装箱堆场基于混堆的滚动式计划堆存方法[J].系统工程学报,2005,20(5):466-471. [WANG B,Method of planned rolling period of a container yard based on mixture storage[J].Journal of Systems Engineering,2005,20(5):466-471.]

[3] 郑红星,杜亮,董键.混堆模式下集装箱堆场箱位指派优化模型[J].交通运输系统工程与信息,2012,12 (1):153-159.[ZHENG H X,DU L,DONG J, Optimization modeloncontainerslotallocationin container yard with mixed storage mode[J],Journal of Transportation SystemsEngineeringandInformation Technology,2012,12(1):153-159.]

[4] Kim H K,Lee K M,Hwang H.Sequencing delivery and receiving operations for yard cranes in port container terminals[J].Int.J.Production Economics,2003,84 (3):283-292.

[5] 韩晓龙.集装箱港口龙门吊的最优路径问题[J].上海海事大学学报,2005,26(2):39-41.[HAN X L. Routing problem of transfer crane at container terminals [J].Journal of Shanghai Maritime University,2005, 26(2):39-41.]

[6] W C Ng,K L Mak.An effective heuristic for scheduling a yard crane to handle jobs with different ready times [J].Engineering Optimization,2005,37(8):867-877. [7] Wenkai L,Yong W,M E H P,et al.Discrete time model and algorithms for container yard crane scheduling [J].European Journal of Operational Research,2009, 198(1):165-172.

[8] Matthew EHP,YongW,WenkaiLi,etal. Development and simulation analysis of real-time yard crane control systems for seaport container transshipment terminals[J].OR Spectrum,2009,31(4):801-835.

[9] 乐美龙,林艳艳,范志强.基于两阶段启发式算法的多场桥作业调度研究[J].武汉理工大学学报,2012, 34(1):60-65.[LE M L,LIN Y Y,FAN Z Q, Research on multi-yard-crane scheduling problem based on two-phase heuristic algorithm[J],Journal of Wuhan University of Technology,2012,34(1):60-65. ]

Yard Crane Scheduling in the Mixture Storage Block Based on Hybrid Genetic Algorithm

ZHENG Hong-xing,YU Kai
(Transportation Management College,Dalian Maritime University,Dalian 116026,Liaoning,China)

The yard crane scheduling problem in the mixture storage container terminal's block involves the allocation of limited yard crane resource and the scheduling of loading and unloading tasks on each block in the mixture storage container terminal,in order to reduce the waiting cost of all tasks and the non-load and non-unload cost of all operating yard cranes during the fixed span,as well as assure those operating yard crane's operation strength not passing the strength limit.Under the real constraints of non-crossing of yard cranes and keeping safe distance when multi-yard cranes are working together,along with different priority level between the inner truck and outer truck,and those trucks'waiting time limit,the non-linear mathematical planning model is set up.A hybrid genetic algorithm(HGA)is proposed according to the characteristics of the problem which is based on the tabu search algorithm,and the chromosome representation is structured on the sequence of tasks.Finally,the model and the algorithm are proved by one real example.

waterway transportation;systems engineering;yard crane scheduling;hybrid genetic algorithm;mixture storage container terminal's block

U693

: A

U693

A

1009-6744(2013)05-0150-09

2013-01-28

2013-05-10录用日期:2013-06-14

国家自然科学基金(71202108);中央高校基本科研业务费专项资金(017229).

郑红星(1971-),男,河北迁安人,博士,副教授.

*通讯作者:zhredstar@yahoo.cn