考虑场桥效率的集卡失约优化仿真

赵 旭，张宝国，索 浩

(大连海事大学交通运输工程学院，辽宁大连 116026)

1 引言

近年来，由于我国日益完善的集装箱港口硬件设备，集装箱吞吐量快速增加，港口堆场集装箱进出口流动大，这对集卡的运输效率提出了更高的要求，集卡预约系统能够降低集卡港内周转时间和排队等待时间，但是受客观因素影响，有部分集卡难以在预约时间段到达，这就造成了集卡的失约现象。现实情况中，集卡预约系统的实施效果是受到现实因素干扰的，比如交通堵塞、天气变化等带来的不确定性因素，增加了集卡的失约率，干扰了以降低排队时间为目标的集卡预约系统，并且一旦失约集卡的数量过多，甚至会造成原本预约模式的不可行。在集卡预约系统中，集卡的早到和晚到或未预约集卡的进入港口都会对港口的服务水平产生影响。这种干扰会造成港口设备的重叠使用，并且增加集卡的港内周转时间，并且造成集卡公司的营运成本增加。

国内外学者在集卡预约方面己开展了众多前沿性的研究，取得了重大进展。一些研究致力于评价集卡预约系统的效果[1]，典型研究如Giulianoa和Erera[2]分析了集卡预约系统对闸口排队和碳排放的影响。Namboothiria和Erera[3]以最小运输成本为目标构建了集卡调度模型，研究了集卡预约对集卡车队的影响。Zhao和Goodchild[4]则考虑堆场翻箱，得出集卡预约可以降低堆场翻箱率。

为提高集卡预约系统效率，一些学者针对预约系统的设计与优化问题开展了研究。如，Huynh和Walton[5]通过仿真集卡在集装箱码头的作业过程，以码头和集卡车队效益最大为目标，通过设定实施目标，利用数学模型获得每个时间段可接受的最大集卡数量。由于集卡到达的随机性，刻画集卡到达闸口的过程较为复杂，一些学者针对码头集卡服务排队问题开展了研究，Guan和Liu[6]利用M/EK/c排队模型计算集卡的排队的平均队长，在此基础上构建了预约优化模型。集卡预约系统属于随机服务系统，准确把握集卡排队规律是预约决策的基础，由于集卡到达具有随时间变化的非稳态特征，传统的稳态排队模型虽然可得到集卡排队的平均情况，但不能准确反映集卡的到达规律，为解决此问题，非稳态排队论逐渐得到应用，如Chen[7]建立集卡预约优化模型，利用非稳态排队模型计算集卡在闸口的等待时间，以此为依据优化集卡预约份额。

这些研究为集卡预约实践提供了理论基础，但仍然存在以下问题：1)集卡预约系统没有将失约现象作为重要影响因素；2)失约现象下集卡在闸口和堆场等待时间如何计算；3)能否调整闸口和堆场效率来降低失约带来的损耗。

基于上述问题，本文以揭示预约机制下的集卡到达与服务规律、考虑集卡失约的情况最小化集卡等待时间为目标，运用马尔可夫、排队论和干扰管理等理论，将失约作为主要的影响因素，以集卡等待时间最小化为目标，利用python进行仿真进行深入探讨并详细的数值分析。

2 模型建立

2.1 问题描述与基本假设

外集卡预约系统旨在降低闸口和堆场拥堵问题，提高港口工作效率，充分利用场桥等资源。预约系统的执行在于集卡公司和码头运营者进行良好沟通，确定每一个时间段集卡到达数，也就是每个时间段的预约份额。预约份额的确定一方面在于货量的多少，另一方面在于码头有多少资源来提供服务。本文不考虑货量，只考虑闸口效率和堆场效率以及场桥的利用率。本文中如无特别指定，集卡统一指外集卡。

本文研究中，外集卡港内工作流程如下所示。如图1。

图1 外集卡港口工作流程

2.2 参数定义和模型建立

B：为预约时段，将一天分成B个时段，即b=1，2，3，…，b每个时间段长为1440/Bmin

T：反映集卡到达具有随时间变化的特征，更能准确地计算排队队长，将每天进一步细分为T个时间段，用来计算队长的最小时间单位，(T>b)

N：一个工作周期内集卡数集合

Mb：第b时段最优化预约的集卡数目，b=1，2，3，…，

Z：闸口数(Z=1)

P：集卡准时按照预约时间到达闸口的概率

CZ：每辆集卡闸口处单位时间的等待损耗

CY：每辆集卡堆场处单位时间的等待损耗

CS：场桥为集卡服务而在系统中逗留的单位时间损耗

Y：堆场集合

g：闸口服务效率

y：堆场服务效率

k：为闸口和堆场服务时间服从的爱尔郎分布的阶数[8]

xi：第i个集卡和第i+1个集卡的预约时间间隔

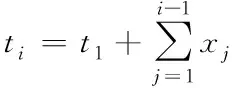
Nb(ti)：b时间段第i个集卡预约时间到达之前系统中的集卡数

λy：单位时间集卡到达堆场的数量

β：计算集卡队长等待成本和场桥在系统中逗留成本的等待系数

p(Nb(ti)=j)：b时间段第i个集卡预约时间到达之前系统中集卡数为j的概率

S(n，p)/M/Z，已知有n个相互独立的预约的集卡，每个集卡以概率p(0，1]按照预约计划S(n.p)到达闸口，且闸口和堆场对集卡提供Markov服务

对于预约排队模型S(n，p)/M/Z，预约的集卡以概率p按时到达而以概率1-p失约。由于闸口不能预知哪些集卡会按时到达而哪些会失约，因此闸口和场桥始终在系统中，期间不进行休假，直到最后一个集卡的预约时间tn为止。若时刻tn时系统仍有集卡未完成任务，则需要服务完所有剩余顾客方可离开系统。

集卡按照预约顺序接受服务且允许预约同一时间。由于允许预约同一时间，所以定义一个规则：预约时间早的顾客如果没有失约则先对其服务。失约集卡相对于没有预约的集卡则先对其服务。

优化具有失约现象的预约排队系统S(n，p)/M/Z(n=2，3)的目的是要使所有按时到达集卡在闸口和堆场的等待损耗和场桥逗留损耗最小，目标是

(1)

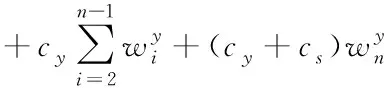
(2)

(3)

2.3 闸口处等待时间计算

P(x1，x2)=

(4)

第一行

(5)

第二行

(6)

第三行

[(1-pe-gx1)](1-pe-gx2)+pe-gx1(1-e-gx2-pgx2e-gx2)*

(1-pe-gx1)pe-gx2+pe-gx1(e-gx2(pgx2+1-p))pe-gx1pe-gx2]

(7)

闸口处集卡等待时间

(8)

2.4 堆场处等待时间计算

闸口和堆场的服务时间服从阶数为k的爱尔郎分布，作业遵循先到先服务(First come first serve，FCFS)，服从参数ky指数分布。根据吴登磊[9]PR指标比法

当服务时间服从k阶的爱尔郎分布，其指标比PR近似和堆场等待时间分别为

(9)

(10)

将参数带入公式可得

(11)

(12)

3 集卡预约的仿真分析

3.1 S(2，P)/M/1的仿真分析

选择天津港集装箱码头分析[8]，闸口和堆场服务时间均服从4阶爱尔郎分布。每b时间段，有两个集卡预约，n=2。每一个集卡以概率p=(0，1]按时到达系统接受服务，失约概率为1-p。当集卡到达服从参数ky指数分布，可以将PR=1。

得到此时的目标函数为

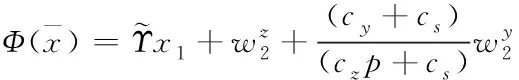
(13)

(14)

将(14)带入(13)可得

(15)

令cy=βcs，y=g=1时函数

(16)

根据matlab显示，β取值不敏感，所以将β=1．

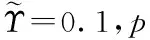
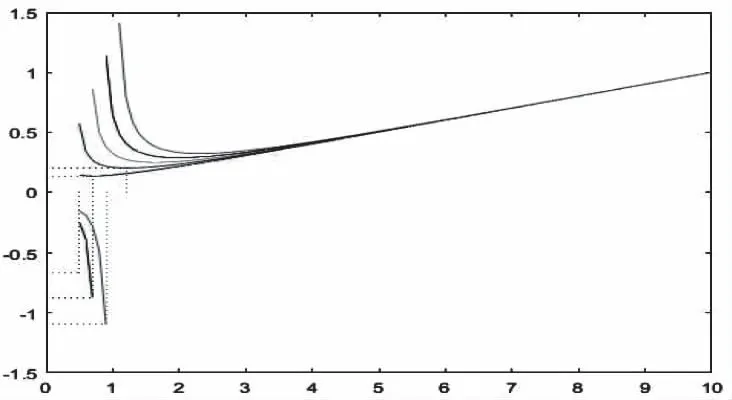
图2 当p=0.1～0.5时候，最低点

图函数图

图函数图

图函数图

图函数图

图函数图

同理可得

图8 当时候，最低点

图9 当时候，最低点

表最优间隔时间和最小成本

表最优间隔时间和最小成本

表最优间隔时间和最小成本

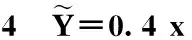
表最优间隔时间和最小成本

表最优间隔时间和最小成本

3.1 S(3，P)/M/1的仿真分析

每个b时段具有三个预约集卡。每一个集卡以概率p∈(0，1]按时到达系统接受服务，失约概率为1-p。当集卡到达服从参数ky指数分布，可以将PR=1.得到此时的目标函数为

(17)

(18)

(19)

图10 p=0.1时Φ(x1，x2)图像

图11 p=0.2时Φ(x1，x2)图像

图12 p=0.3时Φ(x1，x2)图像

图13 p=0.4时Φ(x1，x2)图像

图14 p=0.5时Φ(x1，x2)图像

图15 p=0.6时Φ(x1，x2)图像

图16 p=0.7时Φ(x1，x2)图像

图17 p=0.8时Φ(x1，x2)图像

图18 p=0.9时Φ(x1，x2)图像

图19 p=1时Φ(x1，x2)图像

4 结论

同理，当n=3时，p的临界值时0.5，意味着当失约率超过50%之后，matlab寻找极点时，不得不扩大取值范围，预约系统将不再起作用。

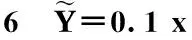
表最优间隔时间和最小成本

5 结束语

本文建立了预约时段下，考虑集卡失约现象的模型。模型给出了集卡在闸口处排队公式和堆场处排队时间计算，具有参考意义。通过matlab仿真，给出了不同失约率情况下集卡等待成本和场桥工作成本的最小值。文中考虑了预约时间段有两辆集卡和三辆集卡的不同情况，并给出了详细计算公式。